A three sided polygon is known as a triangle. A triangle has 3 sides, 3 vertices and 3 angles. There are different ways in which we can categorize the triangles. On the basis of sides, a triangle can be scalene, isosceles, or equilateral. However, in some cases, a triangle may possess unique properties. Such triangles are called special triangles. One such special triangle is the 30°–60°–90° triangles.
What Is a “30-60-90” Triangle?
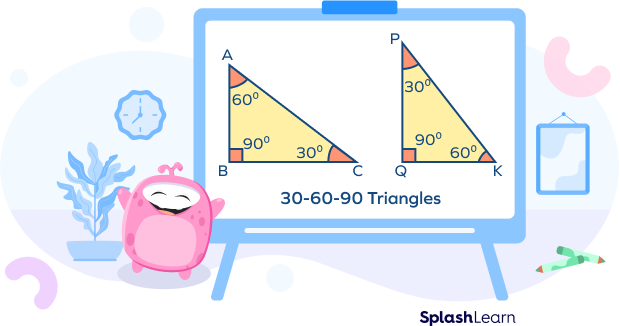
A special right triangle with angles 30°, 60°, and 90° is called a 30-60-90 triangle. The angles of a 30-60-90 triangle are in the ratio 1 : 2 : 3. Since 30° is the smallest angle in the triangle, the side opposite to the 30° angle is always the smallest (shortest leg). The side opposite to the 60° angle is the longer leg, and finally, the side opposite to the 90° angle is the largest side of the right triangle, also known as the hypotenuse.
Since the 30-60-90 triangle is a special triangle, the side lengths of the 30-60-90 triangle are in a constant relationship.
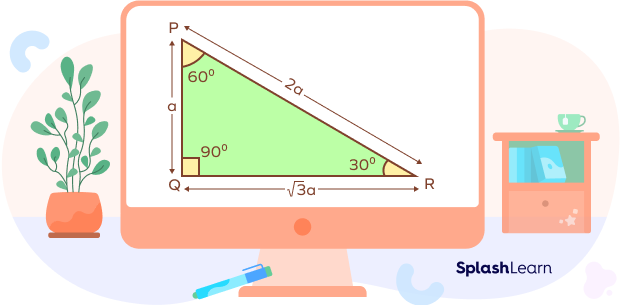
From the figure above, we can make the following observations about the side length ratio of a 30-60-90 triangle:
- The side opposite the 30° angle: PQ = a
- The side opposite the 60° angle: QR = a√3
- The side opposite the 90° angle: PR = 2a
The sides of a 30-60-90 triangle are always in the ratio of 1 : √3 : 2.
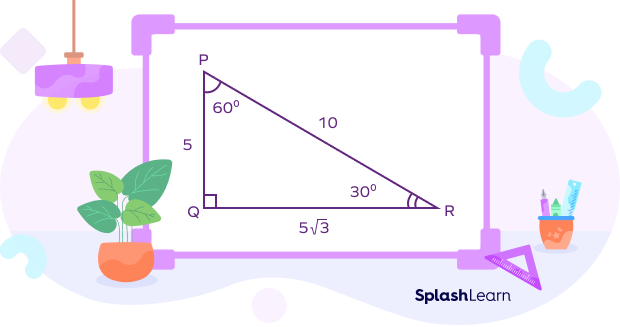
For example:
Here, in triangle PQR,
- The side opposite to the 30° angle is PQ = a = 5 units
- The side opposite to the 60° angle is QR = a√3 = 5√3 units
- The side opposite to the 90° angle is PQ = 2a = 10 units
Recommended Games
30-60-90 Triangle Rule
In a 30-60-90 triangle, we can find the measure of any of the three sides by knowing the measure of at least one side in the triangle. This is known as the 30-60-90 triangle rule. The following shows how to find the sides of a 30-60-90 triangle using this rule:
- When the side opposite to 30° is given.
Consider the side opposite to 30° (shortest side), AB to be ‘a’.
The side opposite to 60°, BC = a√3
The side opposite to 90° (hypotenuse), AC = 2a
- When the side opposite to 60° is given.
Consider the side opposite to 60°, EF to be ‘a’.
The side opposite to 30°, DE = $\frac{a}{\sqrt{3}}$
The side opposite to 90° (hypotenuse), DF = $\frac{2a}{\sqrt{3}}$
- When hypotenuse is given.
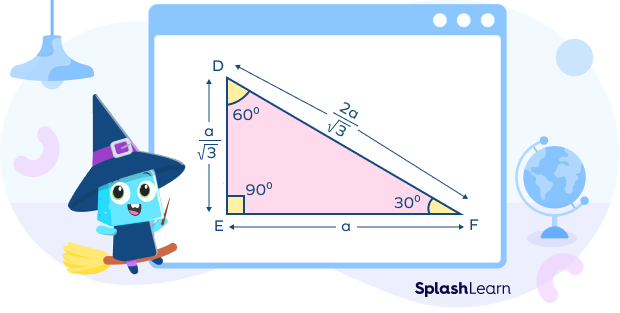
Consider the hypotenuse of the triangle, i.e., PR to be ‘a’.
The side opposite to 30°, PQ = $\frac{a}{2}$
The side opposite to 60°, QR = $\frac{\sqrt{3}}{2}$a
Recommended Worksheets
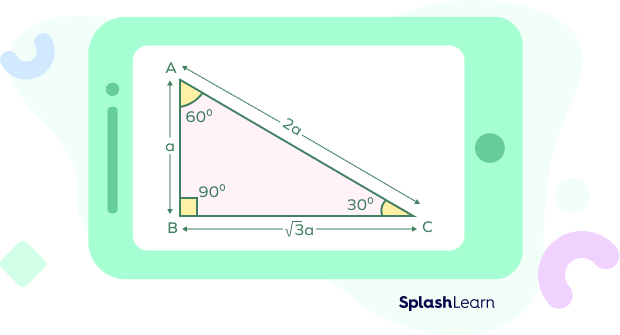
Area of the 30-60-90 Triangle
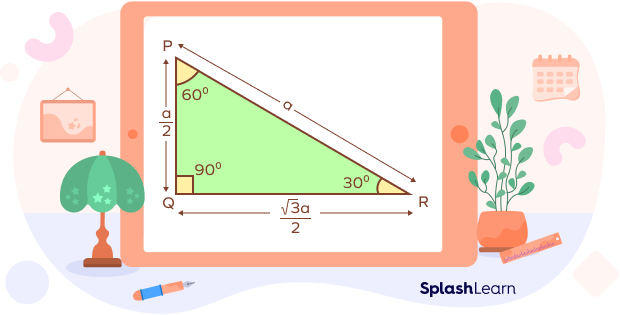
When the perpendicular is given to be a,
Area of $\Delta$DEF = $\frac{1}{2} \times base \times height$
= $\frac{1}{2} \times a \sqrt{3} \times a = \frac{\sqrt{3}a^{2}}{2}$
Conclusion
In this article, we learned about a special triangle, i.e., the 30-60-90 triangle. To read more such informative articles on other concepts, visit our website. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.
Solved Examples
1. Find the length of the side BC in the following figure.
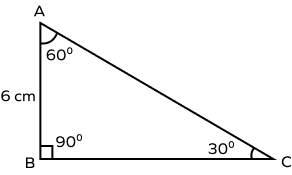
Answer: The side opposite to 30˚ (shortest side), AB = 6 cm
Since the sides of a 30-60-90 triangle are always in the ratio of 1 : √3 : 2.
Therefore, the sides of the given triangle are AB = 6 cm, BC = 6√3 cm and AC = 12 cm.
So, BC = 6√3 cm
2. Find the length of the hypotenuse in the following figure.
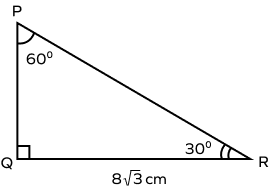
Answer: Side opposite to 60˚, QR = a = 8√3 cm
The hypotenuse of the triangle, i.e., PR = $\frac{2a}{\sqrt{3}} = \frac{2 × 8√3}{\sqrt{3}}$ = 16 units.
3. A triangle has sides 3√2, 3√6, and 3√8. Find the angles of this triangle.
Answer: The sides of the triangle are 3√2, 3√6, and 3√8.
Let us check whether the sides are of the 30-60-90 triangle.
On dividing each side of the triangle by 3√2, we get 1, √3, and 2. Therefore, sides of the triangle are 3√2, 3√6, and 3√8, are in the ratio 1: √3: 2.
The sides are following the 30-60-90 triangle rule. So, the angles of the given triangle are 30°, 60°, and 90°.
Practice Problems
30 60 90 Triangle
Which of the following forms a 30-60-90 triangle?
On dividing the ratio 5 : 5√3 : 10 by 5, we get 1 : √3 : 2. It follows the 30-60-90 triangle rule.
The hypotenuse of a 30-60-90 triangle as shown below is 20 ft. Find the length of the shortest side of the triangle?
In a 30-60-90 triangle, the length of the hypotenuse is twice the length of the shortest side. So, the shortest side of the triangle must be $\frac{hypotenuse}{2}$ = $\frac{20}{2}$ = 10 ft
What will be the area of the triangle if the base is given to be 4√3 cm?
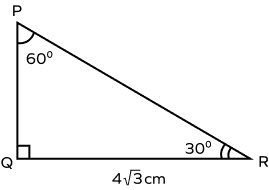
Base is 4√3 cm and perpendicular must be 4 cm. So, Area of the triangle = $\frac{1}{2} \times 4 \times 4√3 = 8√3 cm^{2}$
Frequently Asked Questions
How is the 30-60-90 triangle similar to 45-45-90?
These are some similarities between the 30-60-90 triangle and 45-45-90 triangle.
- Both are right-angle triangles.
- Both follow Pythagorean theorem.
- Sum of the interior angles of both are 180 degrees.
What is the perimeter of a 30-60-90 triangle?
Let the perpendicular be a.
Base = 3a
Hypotenuse = 2a Perimeter = Sum of all the sides = a+3a+2a = a(3+3) units
Which side is the longer leg of a 30-60-90 triangle?
The long leg of a 30-60-90 triangle is the one whose length is greater than the shortest leg and less than the hypotenuse. In other words, it is the side opposite the 60 degree angle.































