What Is a 30 Degree Angle?
A 30 degree angle is an acute angle whose angle measure is exactly 30 degrees. It is an angle obtained by bisecting a 60 degree angle.
An angle is a geometric figure formed when two rays meet at a common point called the vertex.
Recommended Games
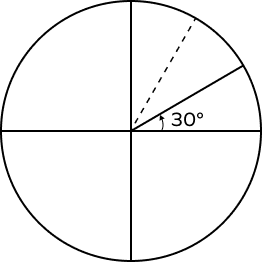
What Does a 30 Degree Angle Look Like?
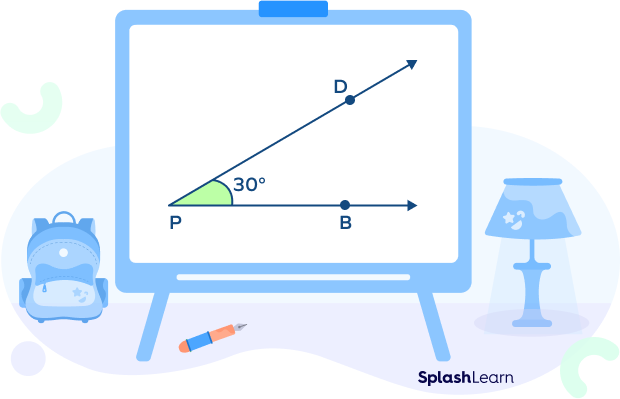
Observe the given diagram. Here, two rays PB and PD form a 30 degree angle at the vertex P.
Recommended Worksheets
How to Construct a 30 Degree Angle with a Protractor
A protractor is a geometric instrument used to measure and construct angles. Here’s a step-by-step guide to construct a 30 degree angle using a protractor:
Step 1: Draw a line segment AB. Align the center of the protractor with the vertex A. Baseline of the protractor is aligned with the line segment AB.
Step 2: Mark the 30 degree angle on the inner scale that starts from 0 on the right side. Name this point as C.
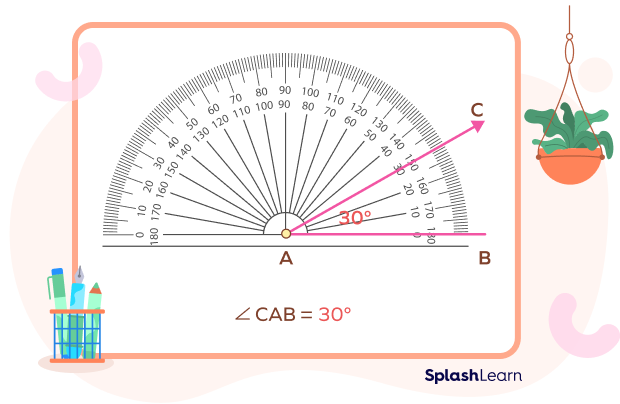
Step 3: Remove the protractor and join the line AC.
How to Construct a 30 Degree Angle with a Compass
Step 1: Draw a ray AB. Keeping A as center and with a suitable radius on the compass, draw an arc on the ray AB that touches the ray AB at the point P.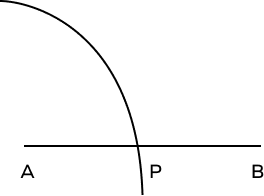 | Step 2: With P as the center and keeping the same radius, draw an arc that cuts the previous arc at point Q. 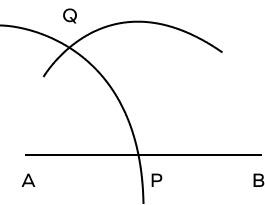 |
Step 3: With P and Q as centers, draw two arcs that intersect each other at point E.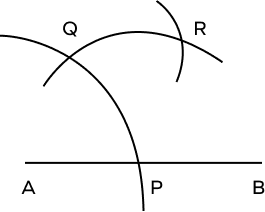 | Step 4: Join points A and R through a straight line. Label this line as AR. ∠RAB=30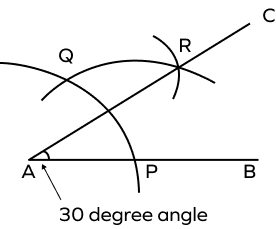 |
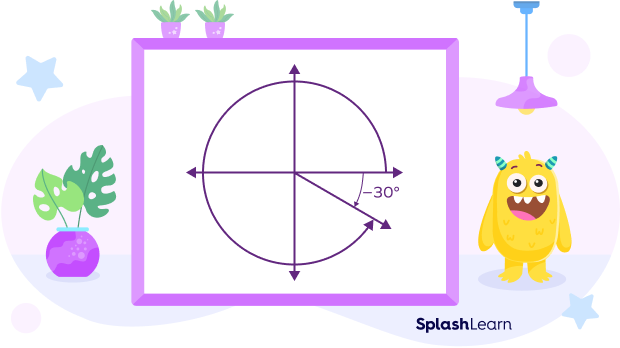
Negative 30 Degree Angle
When the initial arm is rotated clockwise to form an angle, the angle is negative.
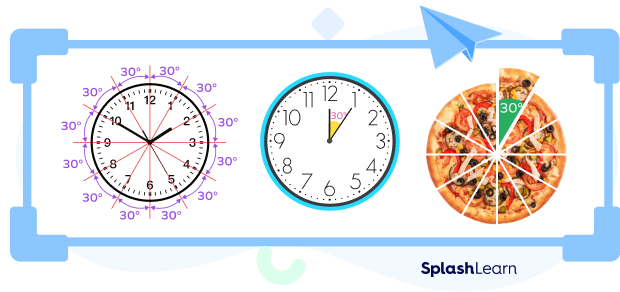
30 Degree Angle in Real Life
There are 12 divisions in an analog clock. Each division represents a central angle of 30 degrees. If you cut a pizza into 12 equal parts, each part represents a central angle of 30 degrees.
Facts about 30 Degree Angle
- The 30 degree angle is one-third of the right angle.
- The complement of a 30 degree angle is a 60 degree angle.
- Six 30 degree angles make a straight angle.
- Twelve 30 degree angles make a complete angle.
Conclusion
In this article, we learned about the 30 degree angle. We discussed how to construct a 30 degree angle using i) protractor and ii) compass. Let’s solve a few examples and practice MCQs based on the concept of 30 degree angle.
Solved Examples on 30 Degree Angle
Example 1: How many 30 degree angles make a right angle?
Solution:
$\frac{90^{\circ}}{30^{\circ}} = 3$
Three 30 degree angles make a right angle.
Example 2: Convert 30 degrees to radians.
Solution:
Let’s convert 30 degrees into radians.
Angle in radians = Angle in degrees $\times \frac{\pi}{180^{\circ}}$
Angle in radians $= 30^{\circ} \times \frac{\pi}{180^{\circ}} = \frac{\pi}{6}$
So, the 30 degree angle in radians is $\frac{\pi}{6}$.
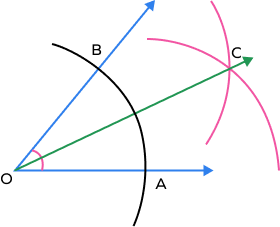
Example 3: Construct a 30 degree angle by bisecting a 60 degree angle.
Solution:
Consider a 60 degree angle with vertex O.
Keeping the compass at the vertex O and with suitable radius, draw an arc intersecting both the arms of the given 60 degree angle at points A and B.
Taking A and B as centers and keeping the radius length more than half of AB, draw two arcs that intersect each other at the point C.
Join O and C.
Here, ∠AOB = 30o
∠AOC = ∠BOC = 30o
Practice Problems on 30 Degree Angle
30 Degree Angle - Construction With Compass and Protractor, Examples
The 30 degree angle is
The 30 degree angle is an acute angle.
What is a 90 degree angle called?
The 90 degree angle is called the right angle.
hat angle will be obtained on the bisection of a 30-degree angle?
Bisection of the angle means dividing it into two halves. Hence, half of the 30 degree angle is a 15 degree angle.
Frequently Asked Questions about 30 Degree Angle
What are acute angles?
Acute angles are angles that measure less than 90 degrees.
Is the 30 degree angle an obtuse angle?
The 30 degree angle is not an obtuse angle. It is an acute angle.
What is the value of 30 angle in terms of pi?
$30^{\circ} = \frac{\pi}{6}$
How do you draw a 30-degree angle without a protractor?
Draw an equilateral triangle, where each angle is 60 degrees. Then, bisect one of the angles in the triangle; each half will measure 30 degrees.
Steps:
- Draw the angle bisector: Draw a line from point A to point D. This line bisects the 60-degree angle, creating a 30-degree angle.
- Draw a line segment: Let’s call it AB.
- Construct an equilateral triangle: With point A as the center, draw an arc. Draw another arc from point B with the same radius, intersecting the first arc at point C.
- Bisect the angle: With points B and C as centers, draw arcs of equal radius intersecting at point D.































