45°-45°-90° Triangle: Properties, Formulas, Construction

What Is a 45°-45°-90° Triangle?

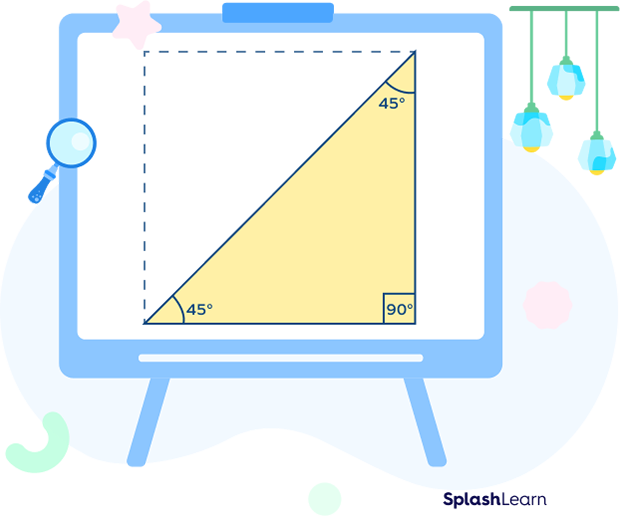
The $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle, as the name itself suggests, is a triangle in which there is one $90^\circ$ angle (right angle), and two $45^\circ$ angles. 

Since two angles are congruent, the sides opposite to the congruent angles are also congruent. Two congruent sides and one right angle make the $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle an isosceles right triangle. 

These triangles have special significance in geometry because they follow properties of right triangles as well as isosceles triangles.

$45^\circ\;-\;45^\circ\;-\;90^\circ$ Triangle: Definition

A $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle is an isosceles right triangle. It is a special type of right triangle in which the three interior angles are $45^\circ,\; 45^\circ,$ and $90^\circ$.

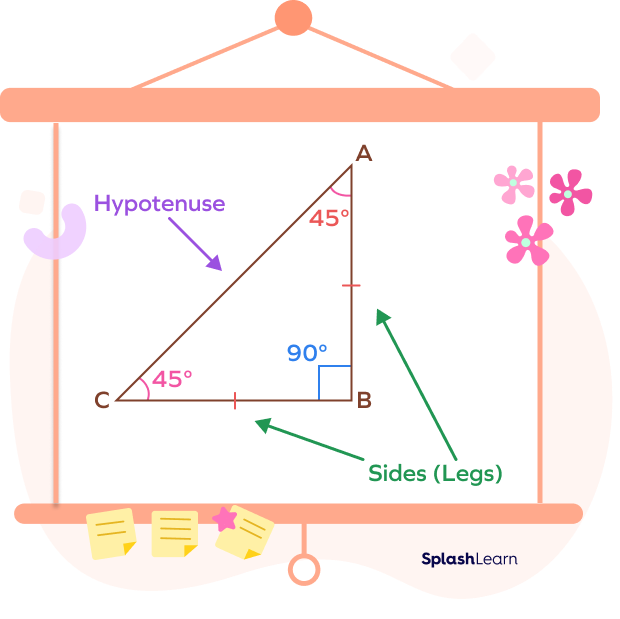
The side opposite to the right angle is called hypotenuse. It is the longest side of any right triangle. Here, AC is the hypotenuse. It is the longest side of the triangle. 

The sides opposite to the $45^\circ$ angles are congruent. They are also known as legs of the right triangle. Here, $AB = BC$.

45°-45°-90° Triangle Theorem

The 45°-45°-90° triangle theorem states that the length of the hypotenuse of a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle is equal to square root times the length of a leg.

Consider a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle ABC.

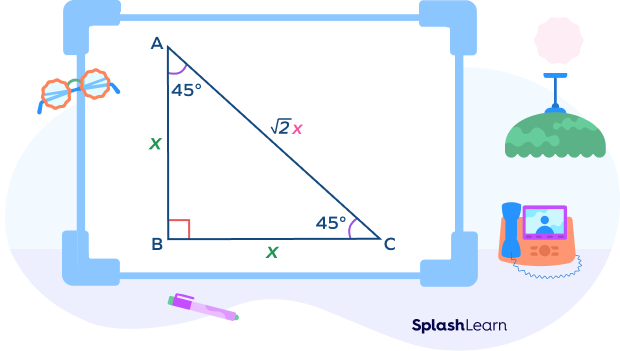
Suppose that the lengths of the congruent sides (legs) triangle is x.

Thus, we have 

$AB = x$ and $BC = x$

We can find the length of the hypotenuse AC using Pythagoras’ theorem.

$AC^2 = AB^2 + BC^2$

$AC^2\; Hypotenuse^2 = x^2 + x^2 = 2x^2$

Thus, length of the hypotenuse $= AC = \sqrt{2x}$

45°-45°-90° Triangle Ratios

The ratio of side lengths in a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle $= AB : BC : AC$

 $= x : x : \sqrt{2x}$

 $= 1 : 1 : \sqrt{2}$

Ratio of angles in a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle is $45^\circ: 45^\circ: 90^\circ = 1 : 1 : 2$

How to Solve a 45°-45°-90° Triangle

To solve a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle means to find the length of the missing sides when the length of one side of the right triangle is given. We can find the triangle’s perimeter and the triangle’s area, too. 

There are two cases that we consider.

1. To calculate the hypotenuse when the length of one of the sides is given.

This can be calculated by multiplying the given side by 2.

Hypotenuse $= \sqrt{2} \times Leg = \sqrt{2x}$

2. To calculate the length of the equal sides of the triangle when the length of the hypotenuse is given.

We know that the ratio of side lengths in a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle is $1 : 1 : \sqrt{2}$. The length of the equal sides can be calculated by just dividing the length of the hypotenuse by 2. 

45°-45°-90° Triangle Formulas

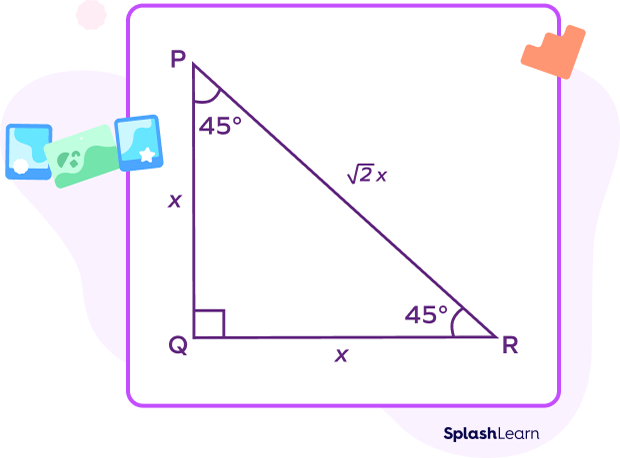
Suppose that the length of one leg in a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle is x. Let’s discuss different formulas associated with this triangle.

Other Leg

If the length of one leg is x units, then the length of the other leg will also be x units. Two legs of a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle are equal.

Hypotenuse

The length of the hypotenuse a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle $= \sqrt{2}\times Side = \sqrt{2x}$ 

Area

We know that the area of triangle is calculated by the formula $\frac{1}{2} \times$Base $\times$Height.

In a  $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle, base $= x$, height $= x$.

Area of a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle $= \frac{1}{2} \times x \times x = \frac{x^2}{2}$

Perimeter

The perimeter is the sum of the sides of the triangle.

Perimeter of a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle $= x + x + \sqrt{2x} = x(2 + \sqrt{2}$.

45°-45°-90° Triangle Rules and Properties

• It has one $90^\circ$ angle and two $45^\circ$ angles. 

• The $45^\circ\;-\;45^\circ\;-\;90^\circ$ right triangle is the only possible right triangle that is also an isosceles triangle.

• Sides opposite to the $45^\circ$ angles are equal.

• The side opposite to the $90^\circ$ angle is the hypotenuse and it is the longest side.

• Since there are two equal sides, the $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle is an isosceles right triangle.

• The ratio of $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle sides equals 1 : 1 : $\sqrt{2}$.

The ratio of $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle angles equals 1 : 1 : 2.

• This triangle has only one line of symmetry .

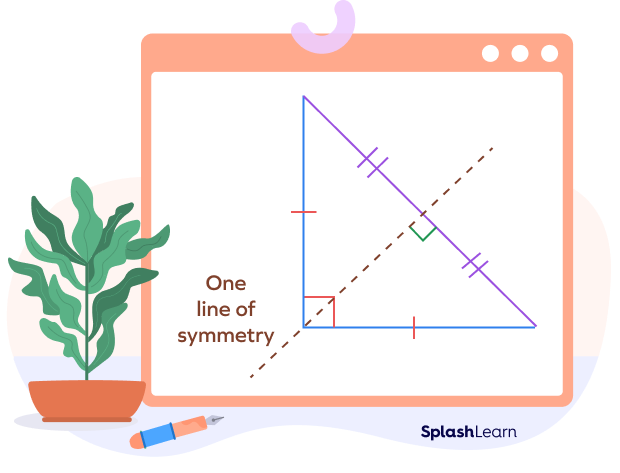
We can see the line that passes through the vertex which has a 90-degree angle and is perpendicular to the opposite side is the line of symmetry because it acts as a mirror, i.e., the figure on either side of the line is identical.

• The $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle does not possess a line of rotational symmetry.

• It has the smallest hypotenuse to the sum of the legs ratio. 

It has the greatest altitude ratio from the hypotenuse to the sum of the legs.

How to Construct a 45°-45°-90° Triangle

The $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle with leg x is half of a square having side x. A square has four right angles. When it is cut diagonally, two right-angled triangles. Both angles are $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangles: one original $90^\circ$ angle of the square, and the other two $90^\circ$ angles bisected that give a $45^\circ$ angle each.

The diagonal of a square becomes the hypotenuse of a right triangle.

Step 1: Construct a square that has the same length as the length of the legs of the triangle we want to construct.

Step 2: Draw one diagonal of the square.

This creates two congruent $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangles and the diagonal becomes the hypotenuse of the triangle.

Facts about 45°-45°-90° Triangle

• Carpenters, architects, and surveyors utilize right triangles to assure “square corners.”
• All the $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangles are similar triangles. This is verified by the AA method of similarity which says that if two triangles have 2 angles of the same degree each they are similar.
• This triangle can be viewed as exactly half of a square having each side length as the length of the legs of the triangle.

Conclusion

In this article, we learned about the $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle, its properties, construction, the ratio of interior angles, the ratio of sides, and different formulas associated with the triangle. Let’s apply these concepts to solve a few examples and practice problems.

Solved Examples on the 45°-45°-90° Triangle

1.  The hypotenuse of a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle is $4\sqrt{2}$ inches. Find the length of the base and height of the triangle.

Solution: 

Let the length of the equal sides (base and height) be x.

The length of the hypotenuse $= \sqrt{2} \times side = \sqrt{2x}$

$\sqrt{2x} = 4\sqrt{2}$

Thus, $x = 4$

Hence, the length of the base and height is 4 inches .

2. One leg of the $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle is 5 feet. Find the length of the other sides of the triangle.

Solution: 

The length of the leg of the triangle is 5 feet. 

We know that the ratio of the sides equals $1 : 1 : \sqrt{2}$. It means that two legs are congruent and the hypotenuse is $\sqrt{2}$ times the length of the leg.

Thus, other leg $= 5$ feet

Length of the hypotenuse $= \sqrt{2} \times leg$.

Hence, the length of the hypotenuse is $\sqrt{2} \times 5 = 5\sqrt{2}$ feet.

3.  The hypotenuse of the $45^\circ\;-\;45^\circ\;-\;90^\circ$ isosceles triangle is $8\sqrt{2}$ inches. Calculate the area of the triangle.

Solution: 

We know that

Hypotenuse $= \sqrt{2} \times leg = \sqrt{2x}$

$8\sqrt{2} = \sqrt{2x}$.

We have leg $= x = 8$ inches 

Area of the triangle $= x \times x \times \frac{1}{2} = \frac{x^2}{2}$

Area of the triangle $= 8 \times 8\times \frac{1}{2} = \frac{8^2}{2} = \frac{64}{2} = 32$ square inches.

The area of the triangle is $32\; inches^2$.

4.  One of the legs of the $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle has a length of 29 feet. Calculate the perimeter of the triangle.

Solution: 

One leg of the triangle $= 29$ feet

Since two legs of a $45^\circ\;-\;45^\circ\;-\;90^\circ$ triangle are congruent, we have 

other leg $= 29$ feet

The length of the hypotenuse is $29\sqrt{2}$ feet.

To calculate the perimeter, we use the formula $x + x + \sqrt{2x} = x(2 + \sqrt{2})$

Hence, the perimeter would be $29 + 29 + 29\sqrt{2} = 29(2 + \sqrt{2})$.

The perimeter of the triangle is $29(2 + \sqrt{2})$ feet.

5. The shorter side of an isosceles right angled triangle is $9\sqrt{2}$ inches. Find the length of the diagonal of the triangle.

Solution:

The ratio of the sides of an isosceles right angled triangle is $x : x : \sqrt{2x}$. 

We have the given shorter side $x = 9\sqrt{2}$ in

Hence, the hypotenuse $= 9\sqrt{2} \times \sqrt{2} = 9\times2 = 18$ inches.

Practice Problems on 45°-45°-90° Triangle

Frequently Asked Questions on 45°-45°-90° Triangle