What Is ‘A Intersection B Complement’?
The term “A intersection B complement” refers to the set denoted by A ∩ B’. It represents the elements that are in set A but not in set B. It signifies the intersection of set A with the complement of set B.
In other words, it includes the elements that belong to A but are not shared with B. This concept is commonly used in set theory and can help analyze relationships between different sets.
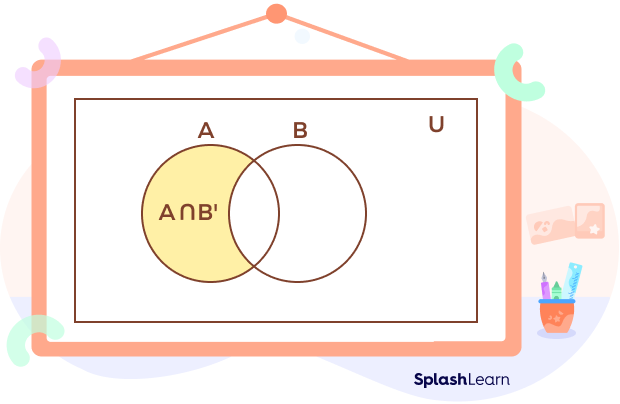
A set is defined as the collection of well-defined objects.
What is A ⋂ B?
The intersection of two sets, indicated by “A ∩ B”, is the collection of elements shared by both sets A and B. In other words, it contains all of the elements found in both sets.
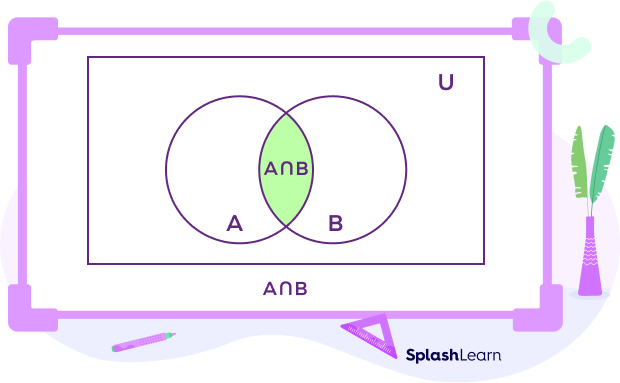
What is the complement of a set?
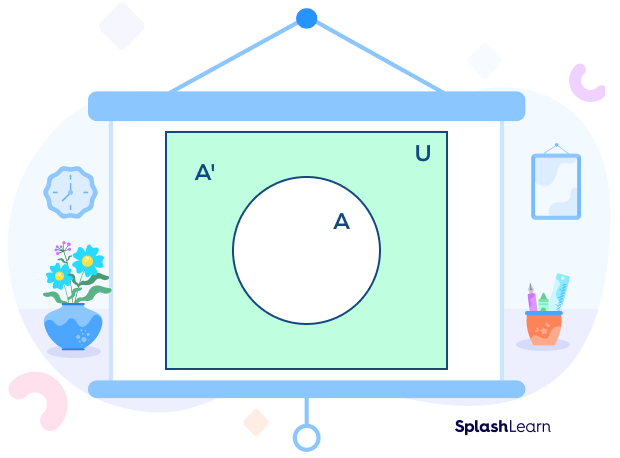
The complement of a set includes all elements that are not in set A but present in the universal set U. In simpler language, the complement of A comprises everything in the universal set that is not A.
Complement of the set A = A’ = A̅ = AC
A’ = U-A
Keeping these definitions in mind, we can easily understand the definition of “A Intersection B Complement” or A ∩ B’. It denotes the set containing all elements from the set A and the complement of the set B.
Recommended Games
‘A Intersection B Complement’ Formulas
The ‘A Intersection B Complement’ formula can be defined as
A ∩ B’ = {x | x ∈ A and x ∉ B}
We can also define the formula as
A – B = A ∩ B’
| Formula | Description |
|---|---|
| A ∩ B’ = A – B | A Intersection B Complement is equal to the A minus B. |
| A ∩ B’ = {x | x ∈ A and x ∉ B} | A Intersection B Complement is equal to the set containing elements in set A but not in set B. |
Example: Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 3, 4, 5}, and B = {4, 5, 6, 7, 8}.
B’ = {1, 2, 3, 9, 10}
A ∩ B’ = {x | x ∈ A and x ∉ B}
A ∩ B’ = {1, 2, 3} …(i)
Also, A – B = {1, 2, 3, 4, 5} – {4, 5, 6, 7, 8}
A – B = {1, 2, 3} …(ii)
A ∩ B’= A – B
Recommended Worksheets
Proof for A ∩ B’ = A – B
A – B represents the set that is formed by removing all the elements of A ∩ B from the set A.
Let x A ∩ B’.
⇔ x ∈ A and x ∈ B’
⇔ x ∈ A and x ∉ B
⇔ x ∈ A but x ∉ B
⇔ x ∈ (A – B)
Thus, A – B = A ∩ B’
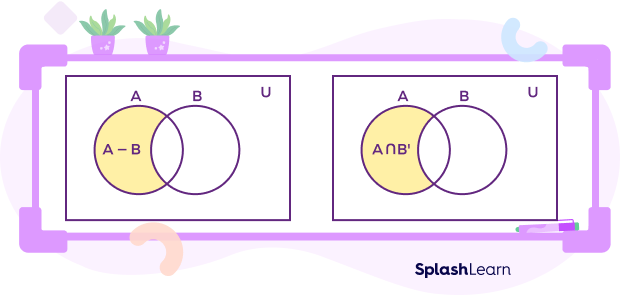
‘A Intersection B Complement’ Venn Diagram
Take a look at the Venn diagram of A intersection B complement.
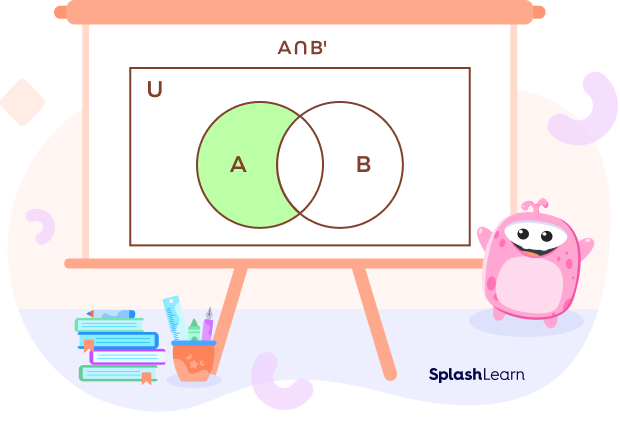
The shaded portion represents elements that are in set A but not in B. It defines the intersection of A and complement of B.
A Intersection B Whole Complement
We define A intersection B whole complement as (A ∩ B)’. It represents the complement of the set (A ∩ B). It is the complement of the intersection of sets A and B.
This refers to the set of all elements in the universal set that are not present in the intersection of sets A and B. In other words, it includes all the elements that do not belong to both A and B simultaneously.
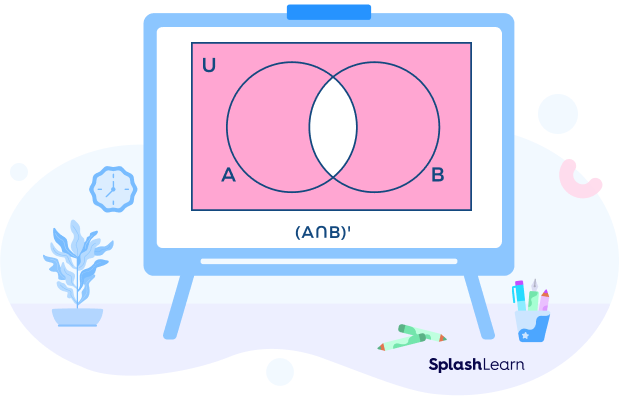
By the De Morgan’s Law, we have
(A ∩ B)’ = A’ ∪ B’
The “A intersection B whole complement” is equal to the union of A complement and B complement.
Facts about ‘A Intersection B Complement’
- A Intersection B Complement has all elements present in the universal set except for the elements in A and not in B.
- The intersection and complement operations have significant importance in multiple areas of mathematics, such as set theory, logic, etc.
Conclusion
In this article, we learned about the set operation A ∩ B’, where we explored the elements that belong to set A but not to set B. Understanding this concept is pivotal for grasping the relationships between sets. Let’s enhance our understanding by solving examples and practicing MCQs.
Solved Examples on ‘A Intersection B Complement’
Example 1: There are two sets, A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7, 8}. What will be the A ∩ B’?
Solution:
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
A ∩ B’ = A – B
A ∩ B’ = {1, 2, 3}
Example 2: In set A = {Apple, Banana, Orange, Mango} and set B = {Banana, Peach, Grapefruit}. Find A Intersection B Complement.
Solution:
A = {Apple, Banana, Orange, Mango}
B = {Banana, Peach, Grapefruit}
A ∩ B’ = A – B
A ∩ B’= {Apple, Orange, Mango}
Example 3: What will be A ∩ B’ if A = {2, 4, 6, 8, 10}, B = {3, 6, 9}, and U = {1, 2, 3, …, 10}?
Solution:
A = {2, 4, 6, 8, 10}
B = {3, 6, 9}
U = {1, 2, 3, …, 10}
B’ = U – B = {1, 2, 4, 5, 7, 8, 10}
A ∩ B’ = {x | x ∈ A and x ∈ B’}
A ∩ B’ = {2, 4, 8, 10}
A ∩ B’ = {2, 4, 8, 10}
Practice Problems on ‘A Intersection B Complement’
A Intersection B Complement - Definition, Formula, Examples, FAQs
Find A ∩ B' of the sets A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7, 8}.
A ∩ B' = A - B = {1, 2, 3}
A ∩ B'=
A ∩ B'={x | x ∈ A and x ∉ B}
(A ∩ B)' =
(A ∩ B)'=A' U B'
Frequently Asked Questions about ‘A Intersection B Complement’
What is a universal set?
A universal set is a collection of all the items relevant to a specific context. It serves as a starting point for considering additional sets in that context. The universal set is a subset of all other sets under discussion. A universal set is often expressed in notation by the sign ξ (Xi) or U.
What is the difference between (A ∩ B)’ or A ∩ B’?
(A ∩ B)’: The complement of the intersection of sets A, and B comprises all the elements that are not shared by both sets A and B but might belong to a bigger universal set. This is also known as the complement of the intersection of A and B.
A ∩ B’: This refers to the intersection of set A with the complement of set B. It encompasses all elements that belong to set A but not set B. This is known as the intersection of A with the complement of B.
Is A ∩ B’ a subset of A?
Yes, all elements in A ∩ B’ are part of set A. They’re the elements that fulfill the criteria of being in A and not in B.




































