Adding Fractions –  Definition With Examples

What is “Adding Fractions”?

Adding fractions can be discussed using two cases: 

• Adding fractions with like denominators
• Adding fractions with unlike denominators

A fraction represents part of a whole. A fraction has two parts: a numerator and a denominator. A numerator represents the parts taken from a whole, written at the top; the denominator represents the number of equal parts the whole is divided into, written at the bottom.

For example, $\frac{5}{6},\; \frac{4}{5},\; \frac{3}{10},\; \frac{8}{9}$, and $\frac{1}{3}$. In the given image, the whole cake is cut into 8 equal pieces. If you take out 3 pieces, they represent the fraction $\frac{3}{8}$.

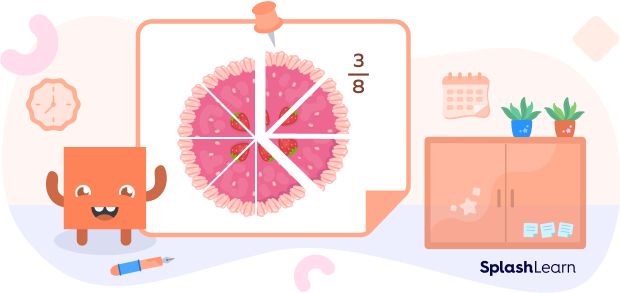
The addition of fractions is the method of finding the sum of two fractions. To add two fractions, we first make their denominators same (by LCM method or by rationalization) and then add the numerators, keeping the new denominator common.

Adding Fractions: Definition

Adding fractions refers to finding the sum of two or more fractions with same or different denominators. 

Adding fractions with the same denominator is simple. We add the numerators and keep the denominator the same.When the denominators are different, we first have to make the denominators same.

How To Add Fractions?

Let us look at the steps for adding two fractions.

Step 1: Check whether the given fractions are like or unlike fractions. Find out whether the denominators are the same. 

Step 2: If the denominator is the same, find the sum of the numerators and place the sum over the common denominator. Simplify the final fraction if required.

Example: $\frac{2}{5} + \frac{1}{5} = \frac{2 + 1}{5} = \frac{3}{5}$

Step 3: If the denominators are different, the fractions are unlike fractions. We will have to convert them into like fractions by making the denominators the same. We will learn different methods to do so later in the article.

What Are Like Fractions and Unlike Fractions?

The fractions that have the same denominator are called “like fractions.”

Example: $\frac{2}{5},\; \frac{1}{5},\; \frac{3}{5},\; \frac{4}{5}$

The fractions that have different denominators are called “unlike fractions.”

Example: $\frac{2}{5},\; \frac{1}{4},\; \frac{1}{2},\; \frac{3}{7}$ 

Adding Fractions with Like Denominators

Adding fractions is the easiest when the denominators of the fractions are the same. Hence, if denominators of two or more fractions are the same, we can directly add their numerators, and keep the denominator the same. 

Example 1: Add the fractions: $\frac{3}{8}$ and $\frac{1}{8}$.

Since the denominators are like, therefore we can add the numerators directly.

$\frac{3}{8} + \frac{1}{8} = \frac{3 + 1}{8} = \frac{4}{8}$

Now, simplify the fraction $\frac{4}{8} = \frac{1}{2}$

Hence, the sum of $\frac{3}{8}$ and $\frac{1}{8}$ is $\frac{1}{2}$.

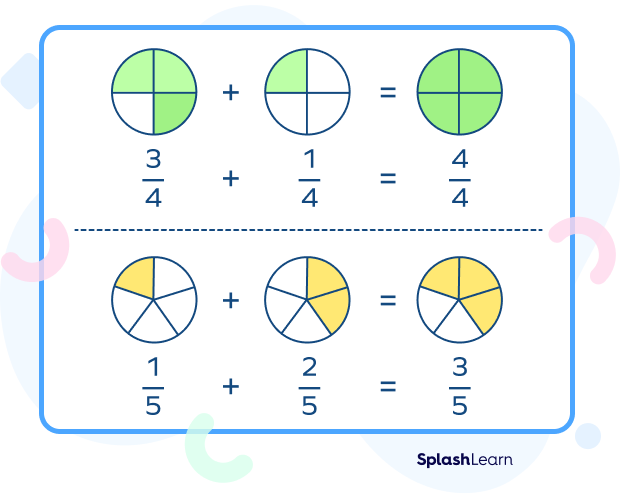
Example 2: $\frac{1}{5} + \frac{2}{5} = \frac{3}{5}$ 

Example 3: $\frac{3}{4} + \frac{1}{4} = \frac{4}{4} = 1$

Adding Fractions with Unlike Denominators

Now that we have learnt how to add like fractions, let us move on to the addition of unlike fractions. When we add two or more fractions with different denominators, then we cannot add the numerators directly. 

Let’s discuss methods we can use to convert the unlike fractions into like fractions.

LCM Method

Let’s solve $\frac{2}{5} + \frac{3}{7}$ using the LCM method.

Here, we are adding two fractions with different denominators.

Find the LCM of the denominators, 5 and 7.

LCM of 5 and $7 = 35$

Multiply 25 by 77 so that the denominator becomes 35.

$\frac{2}{5} \times \frac{7}{7} = \frac{14}{35}$

Now, multiply $\frac{3}{7}$ by $\frac{5}{5}$.

$\frac{3}{7} \times \frac{5}{5} = \frac{15}{35}$

The fractions $\frac{14}{35}$ and $\frac{15}{35}$ are like fractions. 

Now, add the numerators and keep 35 as the denominator.

$\frac{14}{35} + \frac{15}{35} = \frac{29}{35}$

We cannot simplify this further.

Hence, the sum of $\frac{2}{5} + \frac{3}{7} = \frac{29}{35}$.

Cross Multiplication Method

This method works in all cases but when the numerators and denominators of the two unlike fractions are small numbers, the cross multiplication method is convenient to use.

Example: $\frac{3}{7} + \frac{2}{5}$

Adding simple fractions like these is much easier with the cross multiplication method.

• Multiply the numerator of the first fraction with the denominator of the second fraction. 

$(3 \times 5) = 15$

• Multiply the denominator of the first fraction with the numerator of the second fraction.

$(7 \times 2) = 14$

• Add these products together and write the sum as the numerator. Multiply the denominators and write the product as the denominator of the final answer.

$15 + 14 = 29$

$7 \times 5 = 35$

Thus,  $\frac{3}{7} + \frac{2}{5} = \frac{29}{35}$

We can write all the steps together as follows:

$\frac{3}{7} + \frac{2}{5} = \frac{(3 \times 5) + (7 \times 2)}{7 \times 5} = \frac{15 + 14}{35} = \frac{29}{35}$

Adding unlike fractions can be represented visually as follows:

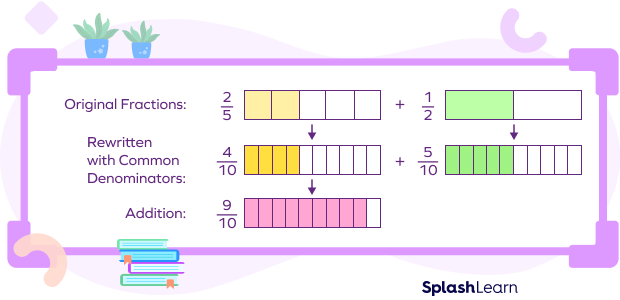
Note that when the denominators of two numbers are co-prime (HCF $= 1$, the denominators that do not have common factors, except 1), we can use the cross multiplication method.

Adding Fractions with Co-prime Denominators

Co-prime or relatively prime numbers are numbers that have only 1 as a common factor. How to add fractions with co-prime denominators? Let’s understand with an example.

Add the fractions $\frac{5}{7}$ and $\frac{3}{4}$.

We see that the denominators 7 and 4 are co-prime because they have only one common factor which is 1. Such fractions can be added easily using the cross multiplication method!

$\frac{5}{7} + \frac{3}{4} = \frac{(5 \times 4 )  + ( 3 \times 7)}{7 \times 4} = \frac{20 + 21}{28} = \frac{41}{28}$

Addition of a Fraction and a Whole Number

Let us learn how to add a fraction and a whole number with the below mentioned steps:

1. Write the given whole number in the form of a fraction (for example $5 = \frac{5}{1}$).
2. Make the denominators the same.
3. Add the fractions.
4. Simplify the sum.

For example: Add \frac{5}{2} + 3$

Here, $\frac{5}{2}$ is a fraction and 3 is a whole number.

We can write 3 as $\frac{3}{1}$.

Now after making the denominators same, we get;

$\frac{5}{2}$ and $\frac{3}{1} \times \frac{2}{2} = \frac{6}{2}$

Now, add $\frac{5}{2}$ and $\frac{6}{2}$.

$\frac{5}{2} + \frac{6}{2} = \frac{11}{2} = 5\frac{1}{2}$

Therefore, the sum of $\frac{5}{2}$ and 3 is $5\frac{1}{2}$.

Adding Mixed Fractions

A mixed fraction is a fraction, which consists of a whole number and a fraction. To add two mixed fractions, first we can convert them into improper fractions and then add them together.

Let’s look at an example to understand it better.

Example: Add : $3\frac{1}{4} + 2\frac{3}{4}$

First, convert the given mixed fractions into improper fractions as shown below.

$3\frac{1}{4}  = \frac{(4 \times 3) + 1}{4} = \frac{13}{4}$ 

$2\frac{3}{4} =  \frac{(4 \times 2) + 3}{4} = \frac{11}{4}$

The fractions are like fractions. 

$\frac{13}{4} + \frac{11}{4} = \frac{13 + 11}{4} = \frac{24}{4} = 6$

Hence, the sum of $3\frac{1}{4}$  and $2\frac{3}{4}$ is 6.

Adding Fractions with Variables

If the numerators of the given fractions have a variable coefficient, we can still add the fractions using the similar steps. 

Example 1: Add $\frac{x}{5} + \frac{2x}{5}$, where “x” is the variable.

Solution: Let us learn how to add these fractions using the following steps:

Step 1: The given fractions, $\frac{x}{5} + \frac{2x}{5}$ are like fractions since they have the same denominator and we can see that “x” is common.

Step 2: We can take out the common factor and rewrite it as: $\frac{x}{5} + \frac{2x}{5} = (\frac{1}{5} + \frac{2}{5})x = \frac{3x}{5}$

Step 3: Therefore, $\frac{x}{5} + \frac{2x}{5} = \frac{3x}{5}$

Example 2:  Add unlike fractions: $\frac{x}{3} + \frac{x}{5}$

Solution: Let us learn how to add the fractions using the following steps.

We know that the given fractions, $\frac{x}{3} + \frac{x}{5}$ are unlike fractions, we will take the LCM of the denominators and convert them into like fractions.

Next, we need to take the common variable out and rewrite it as follows: 

LCM $(3,\; 5) = 15$

$\frac{x}{3} = \frac{x}{3} \times \frac{5}{5} = \frac{5x}{15}$ 

$\frac{x}{5} = \frac{x}{5} \times \frac{3}{3} = \frac{3x}{15}$

We got two fractions with common denominators, $\frac{5x}{15} + \frac{3x}{15} = \frac{5x + 3x}{15} = \frac{8x}{15}$

Therefore, the sum of $\frac{x}{2} + \frac{x}{3} = \frac{8x}{15}$

Note: Different variables, like “x” and “y” are treated as unlike terms.

Formulas For Adding Fractions

Let’s summarize the formulas we discussed for adding fractions.

• Adding fractions with like denominators: $\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}$

• Adding fractions with unlike denominators: $\frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{bd}$

• Adding a fraction and a whole number: $w + \frac{a}{b} = \frac{a + wb}{b}$

Fun Fact!

1. Subtracting fractions also uses the same set of rules as addition of fractions, only the operation is different.

Conclusion

In this article, we learned how to add fractions. We learned how to add like fractions, unlike fractions, mixed fractions, fractions and whole number addition, etc. Now let us solve a few examples on adding fractions along with practice problems to better understand the concepts.

Solved Examples On Adding Fractions

1. What is the sum of $\frac{5}{30}$ and $\frac{10}{30}$?

Solution:

Since, the denominators of the given fractions are equal, the fractions are like fractions.

Add the numerators.

$\frac{5}{30} + \frac{10}{30} = \frac{5 + 10}{30} = \frac{15}{30}$

In the end, we have to simplify the fraction.

$\frac{15}{30} = \frac{1}{2}$

Therefore, the sum of $\frac{5}{30}$ and $\frac{10}{30}$ is $\frac{1}{2}$.

2. What is the sum of $\frac{7}{10}$ and $\frac{4}{15}$?

Solution:

First, we have to check if the given fractions are like fractions or unlike fractions. Since, the denominators of the given fractions are not equal, hence, the fractions are unlike fractions.

Now, let us make the denominator equal by taking the LCM of 10 and 15.

The LCM of 10 and 15 is equal to 30.

Now let us make both the denominators equal.

$\frac{7}{10} \times \frac{3}{3} = \frac{21}{30}$ and,

$\frac{4}{15} \times \frac{2}{2} = \frac{8}{30}$

Now, let us add both the fractions

$\frac{21}{30} + \frac{8}{30} = \frac{21 + 8}{30} = \frac{29}{30}$.

Therefore the sum of $\frac{7}{10}$ and $\frac{4}{15}$ is equal to $\frac{29}{30}$.

3. What is the sum of $\frac{4}{5}$ and 7?

Solution:

Here, $\frac{4}{5}$ is a fraction and 7 is a whole number.

We can write 7 as $\frac{7}{1}$.

Now, after making the denominators same, we get:

$\frac{7}{1} \times \frac{5}{5} = \frac{35}{5}$

Now, add $\frac{4}{5}$ and $\frac{35}{5}$

$\frac{4}{5} + \frac{35}{5} = \frac{39}{5}$

Therefore, the sum of 45 and 7 is 395.

4. What is the sum of $3\frac{2}{5}$ and $6\frac{3}{7}$ ?

Solution:

First, convert the given mixed fractions to improper fractions.

$3\frac{2}{5} = \frac{17}{5}$

$6\frac{3}{7} = \frac{45}{7}$

Make the denominators the same by taking LCM.

The LCM of 5 and 7 is 35.

$\frac{17}{5} \times \frac{7}{7} = \frac{119}{35}$

$\frac{45}{7} \times \frac{5}{5} = \frac{225}{35}$

Now,  add the numerators.

$\frac{119}{35} + \frac{225}{35} = \frac{119 + 225}{35} = \frac{344}{35}$

Hence, the sum of $3\frac{2}{5}$ and $6\frac{3}{7}$ is $\frac{344}{35}$.

5. Add the fractions $\frac{y}{5}$ and $\frac{3y}{5}$.

Solution:

Let us look at the steps to add the fractions:

Step 1: The given fractions, $\frac{y}{5}$ + $\frac{3y}{5}$ are like fractions since they have the same denominator and we can see that “y” is common.

Step 2: We can take out the common factor and rewrite it as: $\frac{y}{5} + \frac{3y}{5} = (\frac{1}{5} + \frac{3}{5})y = \frac{4y}{5}$

Step 3: Therefore, the sum of $\frac{y}{5} + \frac{3y}{5} = \frac{4y}{5}$

Practice Problems On Adding Fractions

Frequently Asked Questions On Adding Fractions