What Is an Angle Bisector?
An angle bisector is a ray or a line that divides an angle into two equal parts. The word “bisector” implies division into two equal parts.
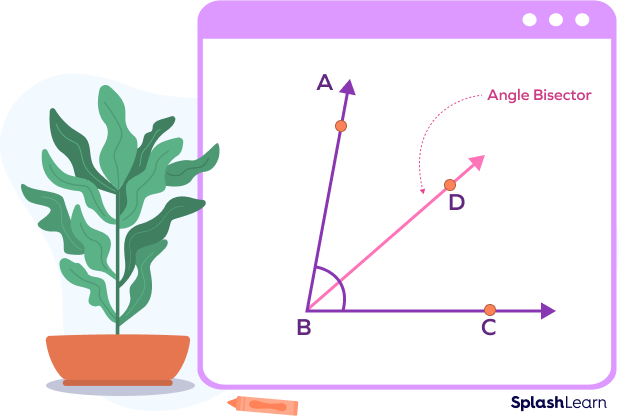
In the following image, $\angle\; \text{ABC}$ is divided into two equal parts by the angle bisector BD.
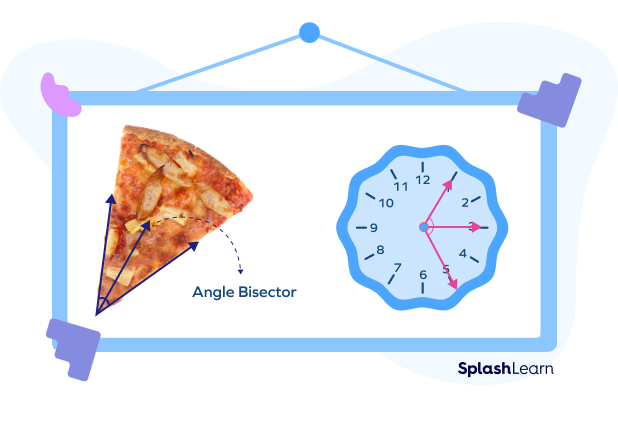
Can you think of examples of angle bisectors in real life? Well, for starters, take a look at a large slice of a pizza cut into equal pieces. Here, the knife acted as an angle bisector. You can also find an angle bisector in a clock, when the angle is made by the minute hand and the hour hand is bisected by the second hand! Keep looking for more such angle bisector examples around you!
Angle Bisector Definition
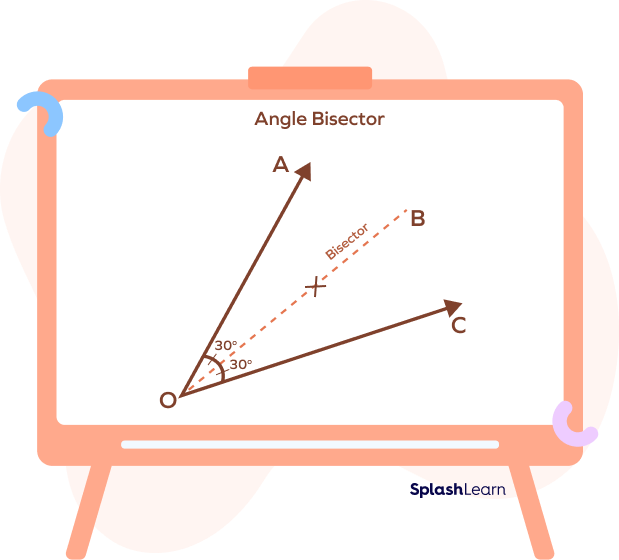
The definition of an angle bisector can be given as a ray or line segment that divides the given angle into two angles of equal measure.
An angle bisector of a $60^{\circ}$ angle will divide it into two angles of $30^{\circ}$ each. It divides an angle into two congruent angles.
Recommended Games
Angle Bisector in a Triangle
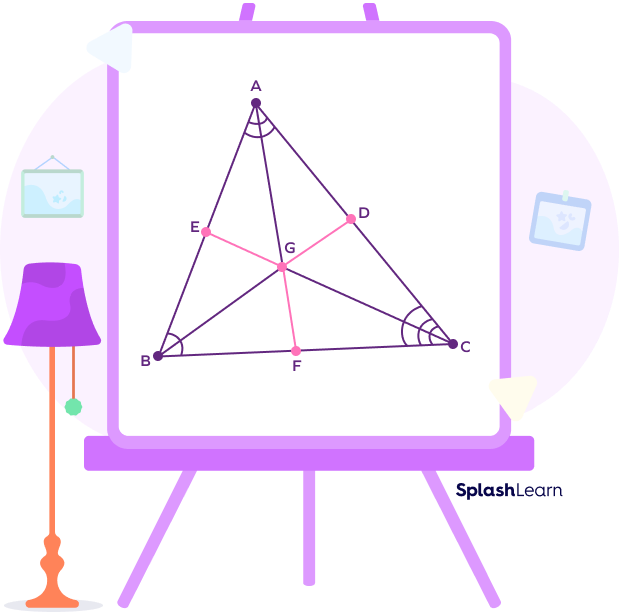
Every triangle has three vertices and three angles. So, there are three-angle bisectors as well—one for each vertex. The point of intersection of these three angle bisectors is called “incenter,” which is equidistant from the sides of a triangle.
In $\Delta\;\text{ABC}$, the segments AF, BD, and CE are angle bisectors, and G is the incenter.
Recommended Worksheets
Properties of Angle Bisector
- An angle bisector divides an angle into two angles of equal measure.
- Any given point lying on the angle bisector is at an equal distance from the arms or sides of the angle.
- The angle bisector in a triangle divides the opposite side in a ratio that is equal to the ratio of the other two sides
How to Construct an Angle Bisector?
Angle bisector construction requires a ruler and a compass. Let’s understand the steps to construct an angle bisector for an angle.
Let’s divide given $\angle\;\text{XYZ}$.

Steps for Construction of an Angle Bisector
- Using a compass, place the pointer at point Y and draw an arc that intersects the two arms of the angle, XY and YZ, at two different points.
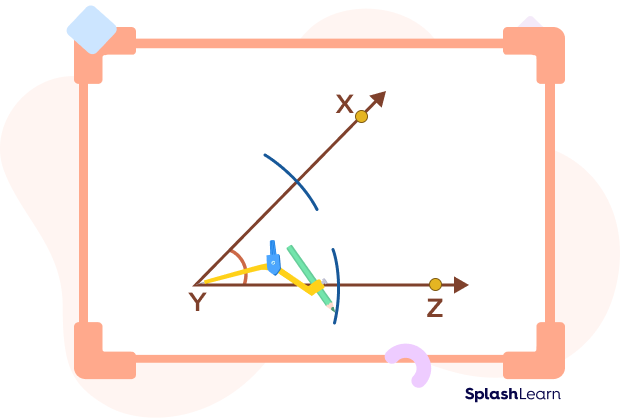
- Next, place the compass pointer where the arc intersects line XY and draw another arc in the interior of the angle.
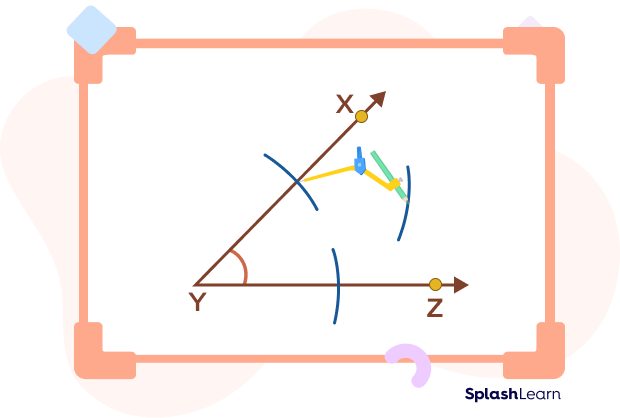
- Without changing the radius of the compass, place the pointer at the point where the arc intersects the arm YZ and draw a similar arc in the interior of the angle such that it intersects the arc drawn in the previous step.
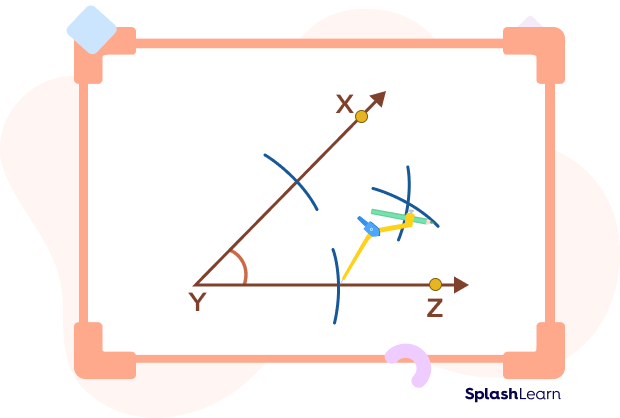
- Now, use a ruler to draw a line from point Y to the point where the two arcs intersect at the interior of the angle.
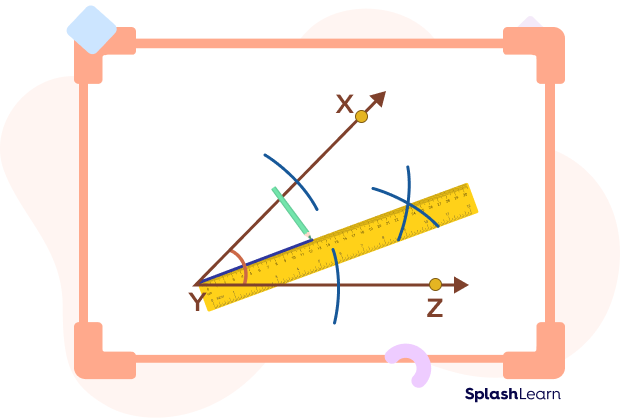
This is how to construct an angle bisector. The line drawn in step 5 is the angle bisector of $\angle\;\text{XYZ}$.
Angle Bisector Theorem
The angle bisector theorem states that an angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle.
Thus, when an angle bisector is drawn from one vertex of a triangle, and it falls on one side of such a triangle, it divides that side in the same ratio as the ratio of the other two sides. We can seek ‘angle bisector theorem proof’ by constructing such a bisector in a triangle.
The following image demonstrates the theorem for reference.
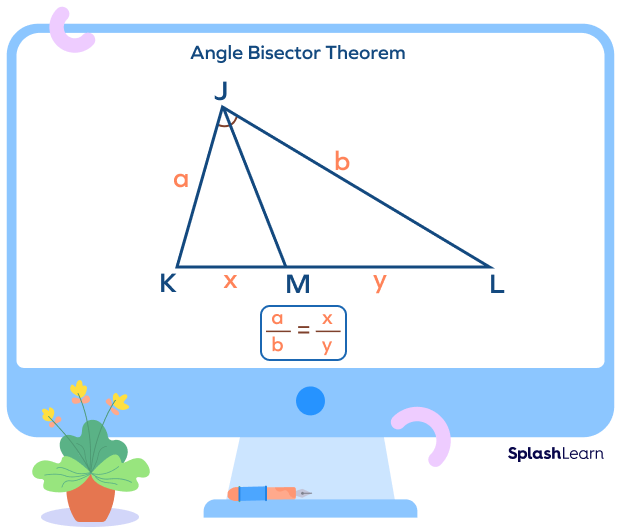
Conclusion
There are many practical examples of an angle bisector, including architectural installations and more. For the construction of an angle bisector in real life, one will need a ruler and a compass. We can also prove the angle bisector theorem by constructing it in real life.
The fun practice problems and solved examples will make it easier for you to understand everything about angle bisectors in great detail. At SplashLearn, learning becomes easier with all the concepts explained in great detail. Join us on the journey to explore the world of math.
Solved Examples on Angle Bisector
1. An angle bisector divides an angle of $80^{\circ}$. What will be the measure of each angle?
Solution:
Given that the measure of the angle is $80^{\circ}$. We know that an angle bisector divides an angle into two equal segments. Each angle will measure $40^{\circ}$.
2. For the image given below, find x if the ray OM is an angle bisector.
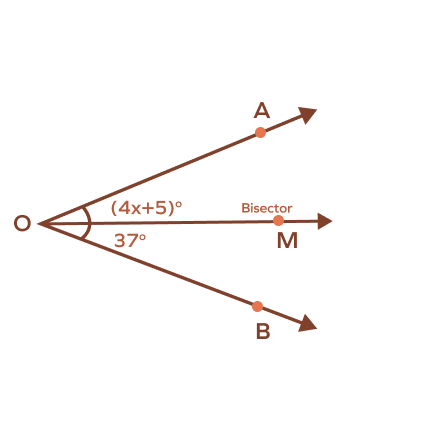
Solution: The value of x is 8.
Since OM is an angle bisector, we know that $\text{m}\;\angle\text{AOM} = \text{m}\angle\;\text{MOB}$.
$4x + 5 = 37$
$4x = 32$
$x = \frac{32}{4}$
$x = 8$
3. For the image given below, m$\angle$AOC $=$ m$\angle$BOC. What can you say about the ray OC?
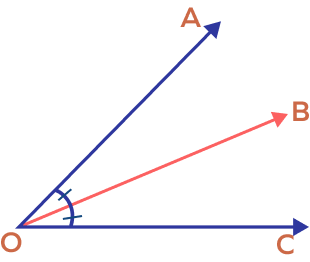
Solution: In the image, m$\angle$AOC $=$ m$\angle$BOC.
So, ray OC is an angle bisector.
4. For the image given below, determine the value of x, if BS is an angle bisector.
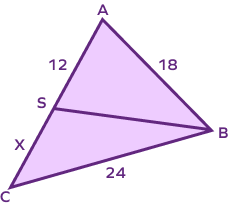
Solution: The value of x is 16.
Here, BS is the angle bisector, which bisects $\angle\;\text{ABC}$.
According to the angle bisector theorem, we can say that ABBC $=$ ASCS
$\Rightarrow \frac{18}{24} = \frac{12}{x}$
$\Rightarrow x = \frac{12 \times 24}{18}$
$\Rightarrow x = 16$
Thus, $x = 16$.
5. In the image given below, if m$\angle$ACF $=$ m$\angle$FCB $=$ 40 and CF is the angle bisector, find m$\angle$ACB.
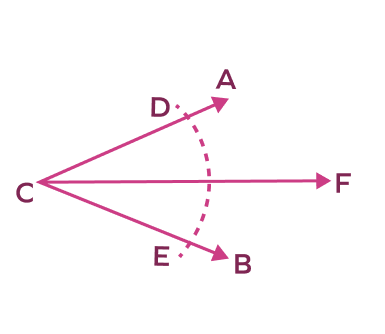
Solution:
We know that an angle bisector divides an angle into two equal sections.
Since $\angle\;\text{ACF} = \angle\;\text{FCB} = 40^{\circ}$, we can say that m$\angle$ ACB $=$ $40^{\circ} + 40^{\circ} = 80^{\circ}$.
Practice Problems on Angle Bisector
Angle Bisector - Definition with Examples
If an angle bisector divides a right angle, what will measure each angle?
Given that the angle is right angle, we know that an angle bisector divides an angle into two equal segments. Hence, it divides the right angle into two angles of measure $\frac{90}{2} = 45^{\circ}$
Determine the value of x if the ray OM is an angle bisector.
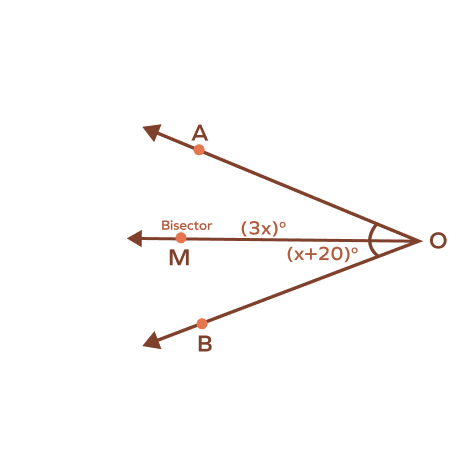
Since OM is an angle bisector, we know that $\angle\;\text{AOM}$ and $\angle\;\text{MOB}$ are equal.
$x + 20 = 3x$
$3x \;–\; x = 20$
$2x = 20$
$x = \frac{20}{2}$
$x = 10$
If an angle bisector divides an angle measuring $15^{\circ}$, what would be the measure of the individual angles thus formed?
Each individual angle will measure half of $15^{\circ}$, that is $7.5^{\circ}$.
The red line represents the angle bisector of a ____ angle.
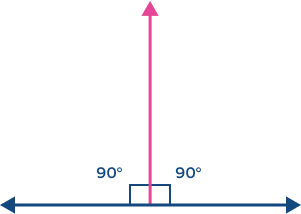
The ray bisects a straight angle into two right angles.
Determine the value of x.
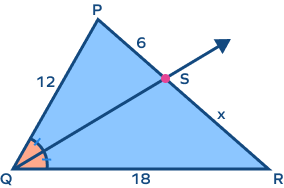
According to the angle bisector theorem, an angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle.
Thus, $\frac{\text{PS}{\text{RS}} = \frac{\text{PQ}}{\text{RQ}}$
$\Rightarrow \frac{6}{x} = \frac{12}{18}$
\Rightarrow x = \frac{18 \times 6}{12}$
$\Rightarrow x = 9$
Frequently Asked Questions on Angle Bisector
How many angle bisectors can an angle have?
A given angle can have only one angle bisector.
How many angle bisectors can a triangle have?
A triangle can have only three angle bisectors since there are only three angles in a triangle.
What is an incenter?
An incentre is a point in a triangle where all three angle bisectors of a triangle meet with each other.
What is the importance of an angle bisector?
When it comes to identifying the corresponding parts of similar triangles, angle bisectors can prove to be very useful. They help to define proofs related to the triangles.





























