Angles of Parallelogram – Definition, Properties, Theorems, Examples

What is Angles of a Parallelogram

A parallelogram has four interior angles that add up to $360^{\circ}$. 

A parallelogram is a special type of quadrilateral that has both pairs of opposite sides parallel and equal. The given figure shows a parallelogram ABCD, which has AB II CD and AD II BC. Also, AD $=$ BC and AB $=$ CD.

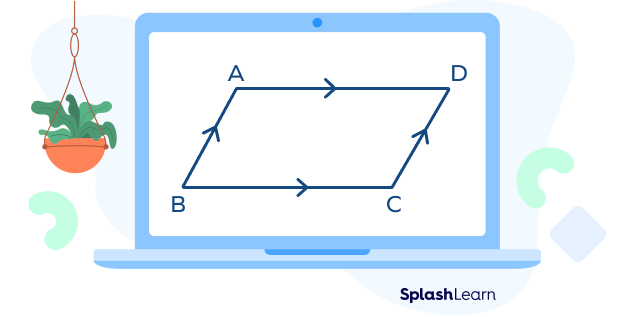
Note that squares and rectangles are special types of parallelograms. In a rectangle, all angles are right angles. A square is both equilateral and equiangular.

Angles of a Parallelogram

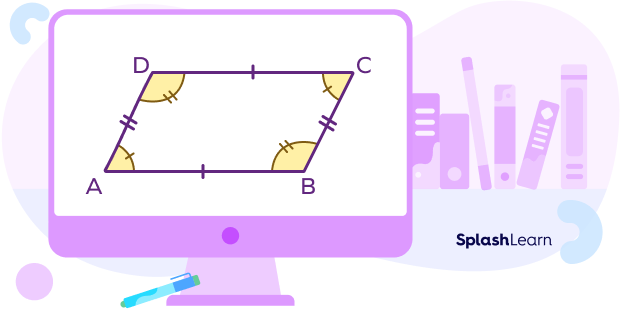
The sum of angles of a parallelogram is $360^{\circ}$. Opposite angles of a parallelogram are of equal measure. Consecutive angles of a parallelogram add up to $180^{\circ}$. 

$\angle A = \angle C$ and $\angle B = \angle D$

$\angle A + \angle B + \angle C + \angle D = 360^{\circ}$

Properties of Angles of a Parallelogram

Here, we are going to study properties of angles of a parallelogram. Observe the following image to understand the important rules of parallelogram angles.

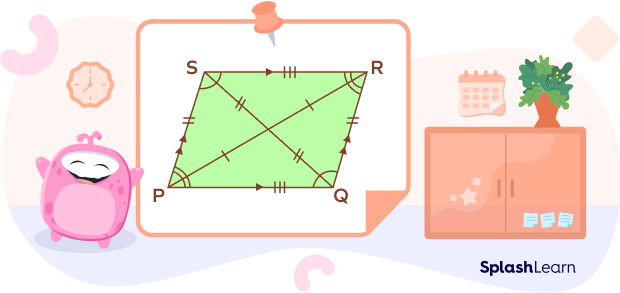
• In a parallelogram, opposite angles are congruent (equal). In the above image, 

$\angle P = \angle R;\; \angle Q = \angle S$.

• All the angles in a parallelogram add up to $360^{\circ}$. Here,$\angle P + \angle Q + \angle R + \angle S = 360^{\circ}$.

• All the respective consecutive angles in a parallelogram are supplementary. 

The supplementary angles in a parallelogram PQRS are as follows:

$\angle P + \angle Q = 180^{\circ}$; 

$\angle Q + \angle R = 180^{\circ}$; 

$\angle R + \angle S = 180^{\circ}$; 

$\angle S + \angle P = 180^{\circ}$

Theorems Related to Angles of a Parallelogram

 Let us learn about the theorems related to the angles of a parallelogram:

1. Opposite angles of a parallelogram are equal.

2. Parallelogram consecutive angles theorem: Consecutive angles of a parallelogram are supplementary.

Theorem 1: Opposite angles of a parallelogram are equal.

Given: PQRS is a parallelogram. 

To prove: $\angle P = \angle R$ and $\angle Q = \angle S$

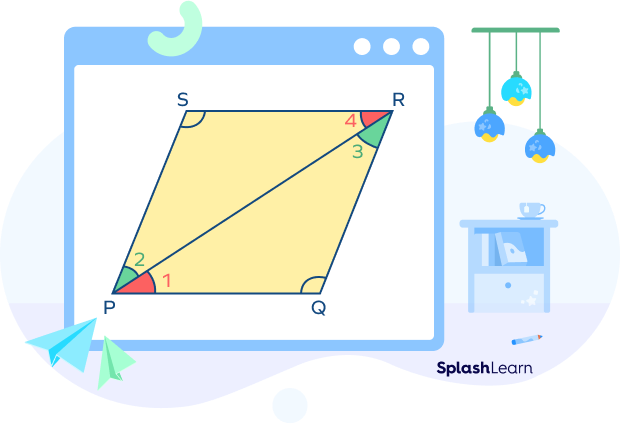
Proof: In the parallelogram PQRS, diagonal PR is dividing the parallelogram into two triangles.

Also, PQ ||  SR and QR ||  PS

Thus, the diagonal PR acts as a transversal.

On comparing triangles PQR and PSR, we have:

PR $=$ PR (common sides)

We know that alternate interior angles are equal.

Thus, 

 $\angle 1 = \angle 4$ (alternate interior angles)

$\angle 2  = \angle 3$  (alternate interior angles)

Thus, the two triangles are congruent, $\Delta\; PQR \cong \Delta\; PSR$

Therefore, $\angle Q = \angle S$ by CPCTC (corresponding parts of congruent triangles are congruent).

Similarly, we can show that $\angle P = \angle R$.

Opposite angles of a parallelogram are equal.

Hence proved.  

Let’s prove the converse theorem as well. 

The converse of the above theorem is as follows:

If the opposite angles of a quadrilateral are equal, then it is a parallelogram.

Given: $\angle P = \angle R$ and $\angle Q = \angle S$

To Prove: PQRS is a parallelogram.

Proof:

We know that the interior angles in a quadrilateral add up to $360^{\circ}$.

Therefore,

  $\angle P + \angle Q + \angle R + \angle S = 360^{\circ}$

Now, we can substitute $\angle R$ with $\angle P$ and $\angle S$ with $\angle Q$ as it is given that

 $\angle P = \angle R$ and $\angle Q = \angle S$

 $= 2(\angle P + \angle Q) = 360^{\circ}$ 

 $= \angle P + \angle Q  = 180^{\circ}$. 

 This shows that the consecutive angles are supplementary. 

 It means that PS || QR.

 Similarly, we can show that PQ || RS.

 Hence, PS || QR, and PQ || RS.

PQRS is a parallelogram.

Hence proved. 

Theorem 2: Consecutive angles of a parallelogram are supplementary.

Given: PQRS is a parallelogram, with four angles $\angle P \angle Q, \angle R, \angle S$ respectively.

To prove: $\angle P + \angle Q = 180^{\circ}, \angle R + \angle S = 180^{\circ}$.

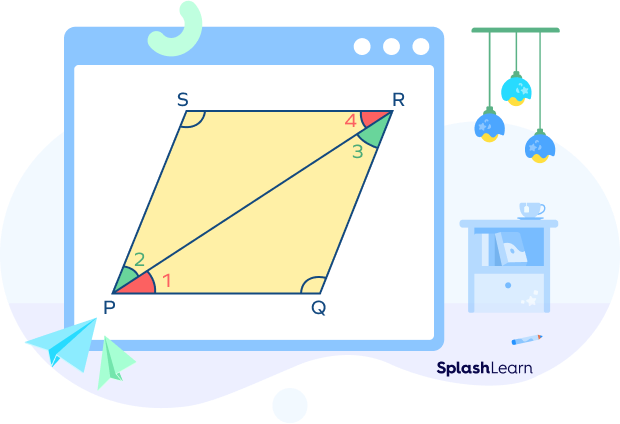
Proof:  

We know that PQ || RS

Consider PS to be a transversal cutting the parallel lines PQ and RS. 

According to the property of transversal, we know that the interior angles on the same side of a transversal are supplementary.

Therefore, $\angle P + \angle S = 180^{\circ}$.

Similarly,

$\angle Q + \angle R = 180^{\circ}$

$\angle R + \angle S = 180^{\circ}$

$\angle P + \angle Q = 180^{\circ}$

Therefore, the sum of the respective two adjacent angles of a parallelogram is equal to $180^{\circ}$.

Thus, the consecutive angles of a parallelogram are supplementary.

  Fun Facts!

• A parallelogram is a special type of quadrilateral that has both pairs of opposite sides parallel and equal.

• As opposite sides of a parallelogram are parallel, they will never intersect.

• Opposite angles of a parallelogram are equal.

• Interior angles of a parallelogram add up to  $360^{\circ}$.

• Consecutive interior angles in a parallelogram (angles that are side by side) are supplementary, i.e., the total of it always equals to $180^{\circ}$

• The diagonal of a parallelogram separates it into two congruent triangles.

• Rectangles and squares are examples of parallelograms that have 90 degree angles, also known as right angles. Rhombuses and squares are examples of parallelograms that have sides of equal length.

• If one angle in a parallelogram is a right angle, then all angles are right angles.

Conclusion

A parallelogram is a special type of quadrilateral that has both pairs of opposite sides parallel and equal and opposite angles are congruent. Now that we have studied the theorems related to angles of parallelogram, let’s solve some examples for better understanding.

Solved Examples on Angles of a Parallelogram

1. In a parallelogram ABCD, if $\angle A = 60^{\circ}$, find the measure of $\angle D$ ?​

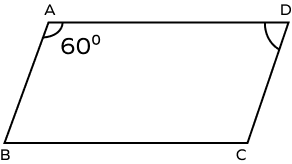
Solution: 

We know that,

Sum of consecutive (adjacent) angles of parallelogram is $180^{\circ}$.

$\angle A + \angle D = 180^{\circ}$

$60 + \angle D = 180^{\circ}$

$\angle D = 180^{\circ} \;-\; 60^{\circ}$

$\angle D = 120^{\circ}$

2. Two adjacent angles of a parallelogram are in the ratio 2:3. Find the measure of the angles.

Solution: 

Let the angles be $2x$ and $3x$.

We know that the adjacent angles in a parallelogram are supplementary.

Thus,

   $2x + 3x = 180$

          $5x  = 180$

           $x =x 36$

  Now, $2x = 2 \times 36 = 72$

   and  $3x = 3 \times 36 = 108$

Thus, the measure of the angles is $72^{\circ}$ and $108^{\circ}$.

3. In the given figure, ABCD is a parallelogram in which $\angle A = 70^{\circ}$. Find the measure of each of the angles.

Solution:

It is given that ABCD is a parallelogram in which $\angle A = 70^{\circ}$.

In a parallelogram, opposite angles are congruent.

Thus, $\angle C = 70^{\circ}$

Since the sum of any two adjacent angles of a parallelogram is 180°,

          $\angle A + \angle B = 180^{\circ}$

          $70^{\circ} + \angle B = 180^{\circ}$

          $\angle B = (180^{\circ} \;-\;  70^{\circ}) = 110^{\circ}$

Angles B and D are opposite angles in a parallelogram.

           $\angle D = \angle B = 110^{\circ}$

Therefore, $\angle B = 110^{\circ},\; \angle C = 70^{\circ}$ and $\angle D = 110^{\circ}$.

4. Two consecutive angles of a parallelogram are $(x + 60)^{\circ}$ and  $(2x + 30)^{\circ}$. Find the measure of the two angles and write the type of parallelogram.

Solution:

We know that the consecutive interior angles of a parallelogram are supplementary.

$\therefore (x + 60)^{\circ} + (2x + 30)^{\circ} = 180^{\circ}$

 $3x^{\circ} + 90^{\circ} = 180^{\circ}$

 $3x^{\circ} = 180^{\circ} \;-\;  90^{\circ}$

 $3x^{\circ} = 90^{\circ}$

  $x^{\circ}  = 30^{\circ}$

Thus, two consecutive angles are $(30 + 60)^{\circ} = 90^{\circ}$ and $2(30)^{\circ} + 30^{\circ} = 90^{\circ}$

We know that, if in a parallelogram one angle is 90 degrees, then all other angles are also 90 degrees.

Hence, the name of the given parallelogram is a rectangle with four right angles.

5. In the parallelogram ABCD given below, find $\angle A, \angle B, \angle C$, and $\angle D$.

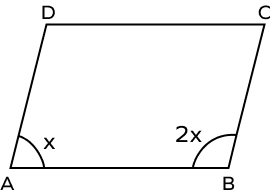
Solution: 

In a parallelogram, adjacent angles are supplementary.

In the above parallelogram, $\angle A$ and $\angle B$ are adjacent angles.

$x + 2x = 180^{\circ}$

   $3x    = 180^{\circ}$

      $x   = 60^{\circ}$

The measure of angle $\angle A$ is

$= x$

$= 60^{\circ}$

The measure of angle $\angle B$ is

$= 2x$

$= 2 \times 60^{\circ}$

$= 120^{\circ}$

According to the properties of parallelogram, the opposite angles are congruent.

          $\angle C =  \angle A$

Thus, $\angle C = 60^{\circ}$

Also,  $\angle B = \angle D$

Thus, $\angle D = 120^{\circ}$

Hence, the measures of $\angle A, \angle B, \angle C$ and $\angle D$ are $60^{\circ},\; 120^{\circ},\; 60^{\circ}$ and $120^{\circ}$ respectively.

Practice Problems on Angles of a Parallelogram

Frequently Asked Questions on Angles of a Parallelogram