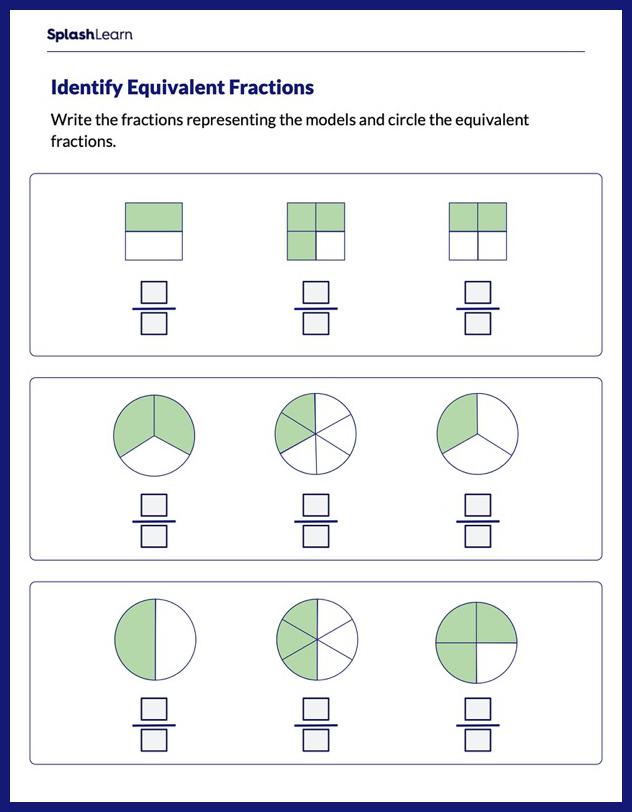
What Is the Area of a Quarter Circle?
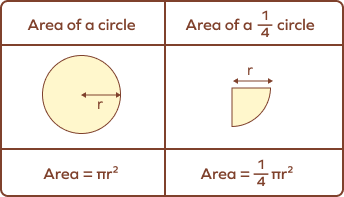
One-fourth of the area of a whole circle is called the area of a quarter of a circle. Area of a quarter circle is also known as the area of a quadrant.
The following image shows division of a circle in four quarters.
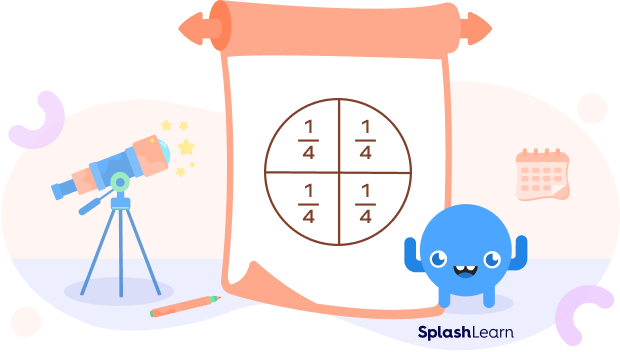
Have you ever noticed how a pizza slice looks after we cut a whole pizza into four equal pieces? This one-fourth part of a circle is called a quarter circle.

A quarter of anything means one-fourth of that object or thing. Thus, by a quarter of a circle, we mean one-fourth of the circle. Four of these shapes will make up a full circle. We can also get a quarter circle by dividing a semicircle into two halves.
Area of a Quarter Circle Definition
In mathematical terms, the area created by two perpendicular radii and one-fourth area of the circumference of a whole circle is called the area of a quarter circle. It is also often referred to as a quadrant. These quadrants are all equal in size and area.
If we divide the area of a particular circle by 4, we can get the area of a quarter circle. It’s that easy!
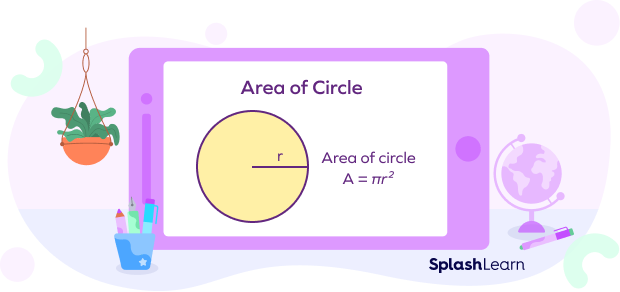
Consider a circle with a radius “r” and a diameter “d.”
We know that the area of a circle is calculated using the formula $\pi r^2$ .
Here,$\pi = 3.14 = \frac{22}{7}$ .
Recommended Games
Area of Quarter Circle: Formula Using Radius
The radius of a quarter of a circle is the same as the radius of the given circle.So let’s say if a circle has a length of radius “r,” then the area of circle $= \pi r^2$.
A quarter circle is $\frac{1}{4}$ of the area of a whole circle.
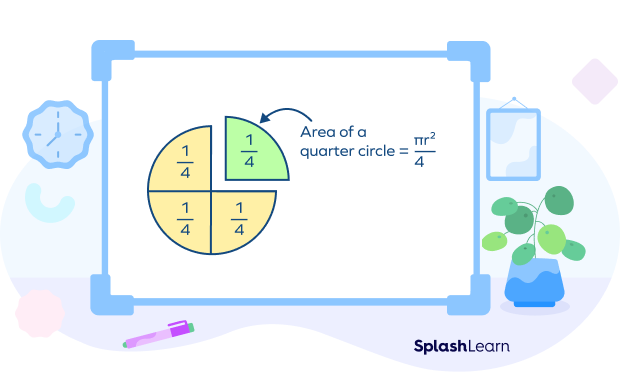
Now, by dividing the area of the whole circle by 4, we can get the formula for a quarter circle.
Thus, the area of a quarter circle $= \frac{\pi r^2}{4}$ or $\frac{1}{4} \pi r^2$.
Recommended Worksheets
Area of a Quarter Circle: Formula Using Diameter
For any circle, its diameter is double of its radius.
Thus, $d = 2r$
We may calculate the area of a quarter circle in terms of diameter by substituting this value into the formula above.
Then, the area of circle $= (\frac{d}{2})^2$
$= \frac{\pi d^2}{4}$
Area of a quarter circle $= \frac{1}{4} \times \frac{\pi d^2}{4}$
$= \frac{\pi d^2}{16}$
Thus, the area of a quarter circle in terms of diameter $= \frac{\pi d^2}{16}$
How To Find the Area of a Quarter Circle
Step 1: Note down the given radius or the diameter of the circle.
Step 2: If the radius “r” is given, substitute the value of “r” in the formula $\frac{\pi r^2}{4}$.
Step 3: If the diameter “d” is given, substitute the value of “d” in the formula $\frac{\pi d^2}{16}$.
Step 4: Area is measured in square units. Don’t forget to assign the appropriate unit to the calculated value of the area of a quarter circle.
Facts about Area of a Quarter Circle
1. A circle is a two-dimensional shape and so is the quarter circle.
2. A quarter circle is formed when a circle is divided into four equal portions.
3. A quarter circle can also be formed by dividing a semicircle into two equal parts.
4. A quarter circle is also known as a quadrant.
5. The circumference of a quarter circle is one-fourth of that of a circle with the same radius.
Conclusion
The area of a quarter circle is one fourth of the area of a circle. In this article, we learned in detail about the area of the quarter circle, formulas. Let’s solve a few examples and practice problems for better understanding.
Solved Examples on Area of a Quarter Circle
1. Linda ordered a 12-inch pizza for herself and her 3 friends. They want to share the pizza equally among themselves. Find the quantity of pizza each one got. (Use $ \pi = 3.14)
Solution:
Given data: The diameter of the pizza $= 12$ inches.
$ \pi = 3.14$
We know that the area of a quarter circle in terms of diameter $= \frac{\pi d^2}{16}$
So, $A = \frac{3.14 \times (12)^2}{16}$
$= \frac{3.14 \times 144}{16}$
$= \frac{452.16}{16}$
$= 28.26$ square inches.
The quantity of pizza each one got is 28.26 $in^2$.
2. Find the area of the quarter circle with the help of the image given below.
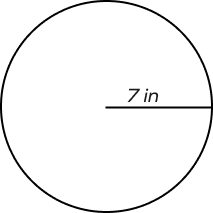
Solution:
Given data:
The radius of the circle $= 7$ inches
We know that the area of a quarter circle in terms of its radius $= \frac{\pi r^2}{4}$
$A =\frac{\pi r^2}{4}$
$= \frac{3.14 \times 7^2}{4}$
$= \frac{3.14 \times 49}{4}$
$= \frac{153.86}{4}$
$A = 38.46$ square inches
The area of the quarter circle $= 38.46\; in^2$
3. The radius of a quarter circle shaped table is 3 ft. What is the area of the table? ( Use $ \pi = 3.14$)
Solution:
Given data:
The radius of the table $= 3$ ft
We know that the area of a quarter circle in terms of its radius $= \frac{\pi r^2}{4}$
$A = \frac{\pi r^2}{4}$
$= \frac{3.14 \times 3^2}{4}$
$= \frac{3.14 \times 9}{4}$
$= \frac{28.26}{4}$
$= 7.065$ square ft.
The area of the quarter circle shaped table $= 7.065\; ft^2$
4. A circular park has a diameter of 50 yards. Only a quarter of the park is allotted for an open gym. Find the area allotted for the gym.
Solution:
Given data: Diameter of the park $= 50$ yards
We know that the area of a quarter circle in terms of diameter $= \frac{\pi d^2}{16}$
So, $A = \frac{3.14 \times(50)^2}{16}$
$= \frac{3.14 \times 2500}{16}$
$= \frac{7850}{16}$
$= 490.62$ square yards
The area of the park allotted for the gym is 490.62 square yards.
Practice Problems on Area of a Quarter Circle
Area of a Quarter Circle: Definition, Formula, Examples
Which of the following is NOT a formula for finding the area of a quarter circle?
$\frac{1}{4}\pi r2$ and $\frac{\pi r2}{4}$ are the formulas for finding the area of a quarter circle in terms of its radius. $\frac{\pi d^2}{16}$ is the formula for finding the area of a quarter circle in terms of its diameter. $\frac{\pi r^2}{2}$ is the formula of the area of the semicircle.
What fraction of a circle is a quadrant ?
A quadrant of a circle is each quarter of a circle. When four quadrants are joined together, it forms a circle.
If the area of a circle is 4 square units, the area of a quarter circle is ________.
Area of a quarter circle is $\frac{1}{4}$ of the total area of a circle. So, if we divide the area of the given circle by 4, we can get the area of a quarter circle. Thus, area of quarter circle $= \frac{4}{4} = 1$.
Which of the following statements is not correct?
A circle is a two-dimensional shape and so is the quarter circle.
Which of the following is the unit of measuring area of a quarter circle?
The unit of area is the square unit, for example, square yards, \[\text{in}^{2}, \text{ft}^{2},\] etc.
Frequently Asked Questions on Area of a Quarter Circle
How to find the area of the part outside of the quarter circle?
Quarter circle is the $\frac{1}{4}$th part of the circle. While outside of the quarter circle is $\frac{3}{4}$th part of the circle. We know that area of quarter circle $= \farc{\pi r^2}{4}$ and the area of the circle $= \pi r^2$. Simply subtract the area of the quarter circle from the area of the whole circle. The final result will be the surface area of the part outside of the quarter circle or the $\frac{3}{4}$th part.
Are the circumference and perimeter of the quarter circle the same?
Yes, circumference is the length of the boundary of the circle. It follows the same principle behind finding the perimeter of any curved geometrical shape.
How can we find the area of a quarter circle in a square?
Take a look at the image given below.
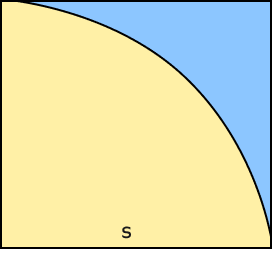
Let the side of the square be s.
Side of the square $=$ Radius of the circle $= \;s\; =$ Radius of the quarter circleArea of a quarter circle $=\frac{\pi r^2} {4} = \frac{\pi s^2}{4}$
What is the perimeter of the quadrant of the circle?
The perimeter of a quadrant of the circle is one-fourth of the circumference of the circle and twice the radius of the circle.Perimeter $(P)$ of a quadrant of a circle $= \frac{2 \pi r}{4} + 2r$
What is the formula to find the arc length of the quarter circle?
The arc length of a quarter circle with radius “r” and diameter “d” is nothing but $\frac{1}{4}$th the circumference of the circle. It is given by $\frac{2 \pi r}{4}$ or $\frac{\pi r}{2}$.