Semicircle: Introduction
In geometry, a semicircle is defined as a half circle formed by cutting the circle into two halves. Every diameter of a circle divides it into two semicircles.
We get a semicircle when we fold a circular piece along its diameter. So, a circle, when divided in two equal halves, gives us a semicircle.
Recommended Games
What Is a Semicircle?
A semicircle is half of a circle. It is a plane figure formed when we divide a circle into two identical halves.
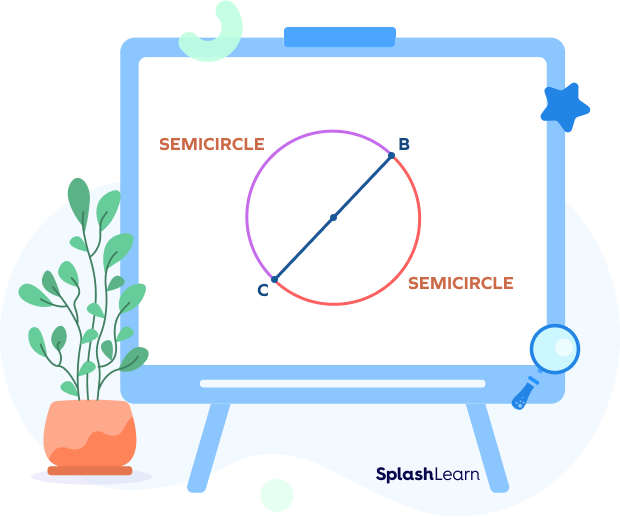
Take any two points on the circle such that the line joining these two points passes through the center of the circle. The two halves that we get are called semicircles. These two semicircles, when taken together, give us a complete circle.
In the following image, O is the center. The diameter BC divides the circle into two semicircles.
Recommended Worksheets
Semicircle Shape
To obtain a semicircular shape, we can simply cut the circle from the center.
So we could also say that the area of the semicircle is just half of that of the circle.
This can be easily understood with the help of the figure given below.
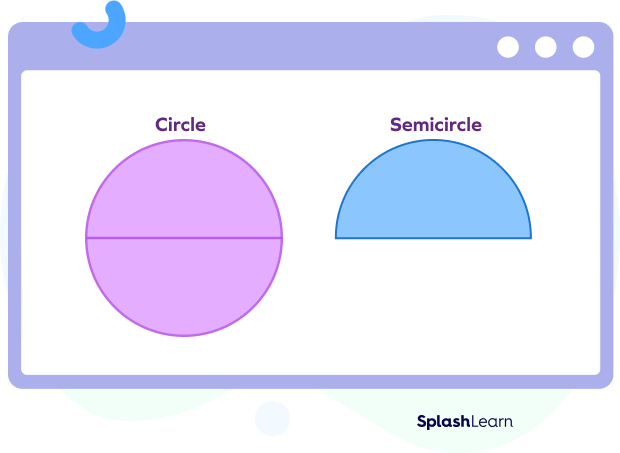
Consider the diameter AB of the given circle. This diameter AB divides the given circle into two identical halves. These halves are semicircles and the area of these two semicircles, when combined, gives the area of the entire circle.
Area of Semicircle
We know that the area of a circle is given by
Area of circle $= \pi r^{2}$
where,
$\pi = 3.1415$ or $\frac{22}{7}$ , and r is the radius of the circle.
The area of the semicircle is half of the area of a circle. This gives us the desired formula, that is,
Area of semicircle $= \frac{\pi r^{2}}{2} = \frac{1}{2} \pi r^{2}$
How to Find the Area of a Semicircle
Step 1: Note the radius of the circle.
If the diameter is given, find the radius by dividing the diameter by 2.
For example, the diameter of the circle is 14 inches, then the radius of the circle is 7 inches.
Step 2: Find the area of the circle using the formula and by substituting the values of r and $\pi$.
$\text{A} = \pi r^{2}$
You can use the value of π as either 3.14 or $\frac{22}{7}$, when not specified in the question.
In our example, $r = 7$ inches and use $\pi = \frac{22}{7}$
So, area of circle $= \pi r^{2}$
area of circle $= \frac{22}{7} \times (7)^{2}$
area of circle $= 22 \times 7$
area of circle $= 154$ square inches.
Step 3: Divide the area of the circle by 2 to obtain the area of the semicircle.
Area of semicircle $= \frac{\pi r^{2}}{2}$
In the above example, Area of semicircle $= \frac{154}{2}$
Area of semicircle $= 77\; \text{inches}^{2}$
Area of a semicircle is measured in “square units.”
Area of a Semicircle Using Diameter
We know that
Area of semicircle $= \frac{\pi r^{2}}{2}$
Here, $r = \frac{d}{2}$
Area of semicircle $=\frac{\pi}{2} \left[\frac{d}{2}\right]^{2}= \frac{πd^{2}}{8}$
Derivation
We know that the area of any shape can also be determined with the help of the number of squares in that particular shape. So, we can say that the area of the circle can be measured by the number of square units fitting in that circle.
Consider a circle shown below, containing isosceles triangles.

All the radii of the circle are equal in length.
So, the polygon in the above figure can be easily divided into various (n) isosceles triangles (radius being two equal sides).
One such isosceles triangle can be represented as given below.
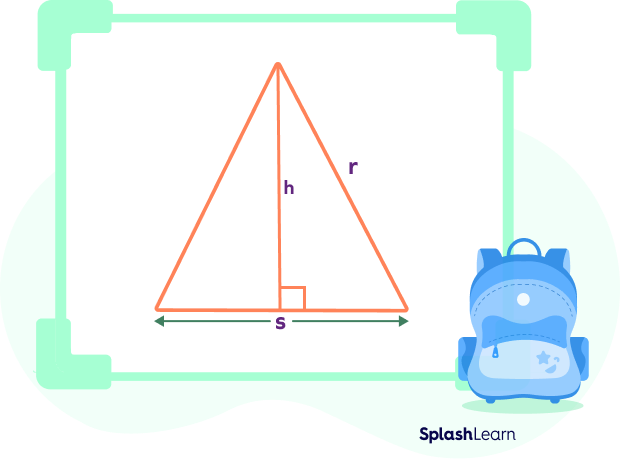
Area of a triangle can be given as half times the product of its height and base.
In this given isosceles triangle, base $= s$ and height $= h$.
The area of this isosceles triangle $= \frac{1}{2} (h \times s)$.
Similarly, for n such isosceles triangles the area would be n times the area of one such triangle.
Area of n such isosceles triangles $= \frac{1}{2} (n \times h \times s)$.
Here, the term $n \times s$ gives the perimeter of the polygon. As the polygon happens to look more and more like a circle, the perimeter term approaches the circumference of the circle, which is given as $2\pi r$.
When we substitute $2 \times \pi \times r$ in place of $n \times s$ we get,
Area of polygon $= 12 (2\pi r)$
Also, as s approaches zero, which happens as the number of sides increase making the triangle narrower, h approaches to r (the value of h becomes very close to r). So we substitute, r in place of h to get:
Area of polygon $= \frac{r}{2} (2 \times \pi \times r)$
Area of polygon $= \frac{r}{2} (2 \times \pi \times r)$
Area of polygon $= \frac{1}{2} (r \times 2 \times \pi \times r)$
Rearrange it to get,
Area of circle $= \pi r^{2}$
We know that the area of a semicircle equation is equal to half the area of the complete circle.
Therefore,
Area of a semicircle $= \frac{\pi r^{2}}{2}$
Area of Semicircle Formula
So we derive the formula for the area of a semicircle as $(\pi r^{2})/2$, which is half the area of a circle.
Also, the surface area of the semicircle formula is the same as the area of the semicircle formula.
Area of semicircle $=\frac{\pi r^{2}}{2}$
Fun Facts!
- Semicircle is obtained by cutting the circle into two exactly equal halves.
- Area of a semicircle is half the area of a circle with the same radius.
- Area of a semicircle with radius r can be given as $(\pi r^{2})/2$.
Conclusion
In this article, we learned about semicircles. We derived the formula for calculating the area of a given semicircle with the help of the area of a circle with a given radius. We also learned a few amazing facts related to semicircles. The concept was complemented by a few solved and a few unsolved questions related to the topic.
Solved Examples
1. If the radius of a semicircle is 49 inches, find its area.
Solution: Area of semicircle $= \frac{\pi r^{2}}{2}$
Area of semicircle $= \frac{22}{7} \times \frac{49^{2}}{2}$
Area of semicircle $= 11 \times 7 \times 49$
Area of semicircle $= 3773\; \text{inches}^{2}$
2. If the diameter of a semicircle is 70 inches, find its area of the semicircle with diameter.
Solution: Area of Semicircle $= \frac{\pi r^{2}}{2}$
Radius $= \frac{70}{2} = 35$ inches.
Now, Area of semicircle $= \frac{22}{7} \times \frac{35^{2}}{2}$
Area of circle $= 11 \times 5 \times 35$
Area of circle $= 1925\; \text{inches}^{2}$
3. Find the area of the figure in which ABCD is a square of side 42 inches and CPD is a semicircle. $(\text{Use}\; \pi = \frac{22}{7})$
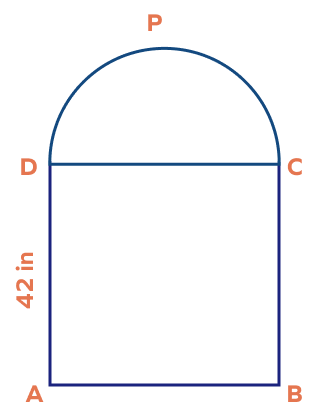
Solution:
The required area $=$ Area of the square $\text{ABCD} +$ Area of the semicircle $\text{CPD}$
$= a^{2} + \frac{1}{2} \pi r^{2}$
$= 42^{2} + \frac{1}{2} \times \pi \times (\frac{1}{2} \times 42)^{2}$
$= (42^{2} +\frac{1}{2} \times \frac{22}{7} \times 21^{2})$
$= 1764 + 693$
$= 2457$ square inches
4. If the area of a circle is 100 square yards, what is the area of a semicircle?
Solution:
Area of circle $= 100$ square yards
Area of semicircle $= \frac{100}{2}$ square yards
5. Hazel has a circular garden outside her house with a diameter of 12 yards. Hazel wants to mow exactly half of the garden. Find the area of the part she wants to mow.
Solution:
Diameter $= 12$ yards
Area $= ?$
Area of a semicircle $= \frac{\pi r^{2}}{2}$
Radius $= \frac{12}{2} = 6$ yards
$\pi = 3.142$
Therefore, area $= \frac{3.142 \times 6 \times 6}{2} = 56.55$ square yards
Practice Problems
Area of a Semicircle
The area of a semicircle is ____ the area of the circle.
Radius of the semicircle is the same as the radius of the circle.
A circle has a diameter of 14 inches. What is the area of the semicircle?
$d = 14$ inches. So, $r = \frac{14}{2} = 7$ inches
Area of semicircle $= \frac{\pi r^{2}}{2}$
Area of semicircle $= \frac{22}{7} \times \frac{7^{2}}{2}$
Area of semicircle $= 77\; \text{inches}^{2}$.
The ____ of circle divides into two semicircles.
The diameter of a circle divides it into two equal parts, which are called semicircles.
Area of the semicircle shown below is ____.
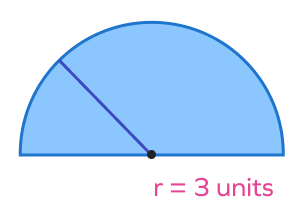
Area of complete circle $= \pi r^2 = 9\pi$
Area of semicircle $= \frac{\pi r^2}{2} = \frac{9\pi}{2}$
Frequently Asked Questions
What is a quarter circle?
If a circle is divided into four equal parts, then each part is called a “quarter circle.” Four quarter circles make a complete circle.
What is circumference?
Circumference is the length of the boundary of the circle.
What is the perimeter or circumference of the semicircle?
Perimeter of the semicircle $= \pi r + d$, where d is the diameter of the circle.