What Is the Average Speed Formula?
The average speed formula is given by the total distance traveled divided by the time taken to cover that distance.
The formula to find average speed is
Average speed $= \frac{Total \;distance}{Time}$
Observe the car in the given image. The distance it covers in the different time intervals is different. The speed of the car is not constant.
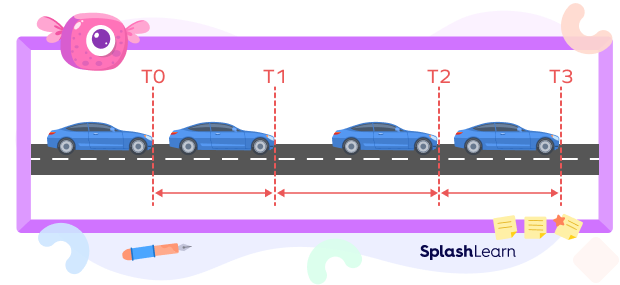
When you travel from one place to another by some vehicle, the speed changes from time to time. You do not travel with the same speed throughout the journey. The average speed, as the name itself suggests, gives us the mean value or the average value of the speed at which you traveled.
It is kind of an estimate to understand the speed by which an object finishes its journey. It provides insights into how fast an object is moving over a given distance and time. Calculating average speed allows us to estimate travel times and make comparisons between different routes or means of transportation.
Recommended Games
Average Speed Formula
The average speed formula can be given by
Average Speed $=$ Total distance covered $\div$ Total time taken

Average speed formula for a round trip
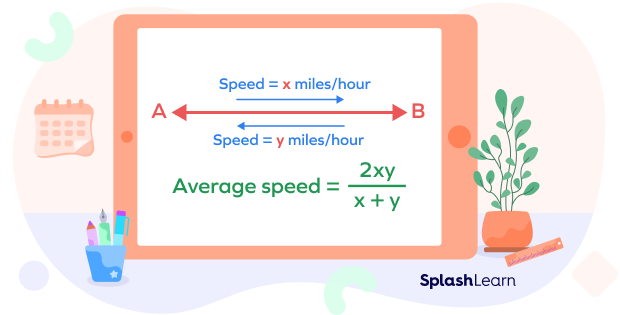
Alt tag: Average speed formula for the round journey
Derivation:
Suppose you travel a distance “d” from A to B with the speed of x miles per hour and the distance from B to A with the speed of y miles per hour. In this case, the same distance is covered (both ways) but with the different speeds. In this case, the average speed is given by
Total distance traveled $= d + d = 2d$
Time taken to go from A to B $= \frac{Distance}{Speed} = dx$
Time taken to go from B to A $= \frac{Distance}{Speed} = dy$
Total time taken $= \frac{d}{x} + \frac{d}{y} = \frac{d(x + y)}{xy}$
Average speed $=$ Total distance covered $÷$ Total time taken
Thus, the average speed equation becomes
Average speed $= \frac{2d}{\frac{d(x + y)}{xy}} = \frac{2xy}{x + y}$
How to Find Average Speed
Let’s understand steps to calculate average speed of an object. Let’s examine the procedure in more detail:
Step 1: Calculate the total distance traveled. If the two different speeds of the given journey are given, calculate the two distances separately using the formula: distance = Speed × time.
Step 2: Calculate the time taken to travel the total distance.
Step 3: Divide the total distance by total time taken to find the average speed. Assign the unit depending on the units of distance and time. For example, if the distance is given in miles and the time is in hours, the average speed will be measured in miles per hour (written as miles/hr).
Example 1: Joy travels the distance of 42 miles in 3 hours and 26 miles in 2 hours. Find his average speed.
Total distance traveled $= 42 + 26 = 68$ miles
Total time taken $= 3 + 2 = 5$ hours
Average speed $= \farc{68}{5} = 13.6$ miles/hr
Example 2: A bus travels the first 3 hours of journey with the speed of 20 miles/hour and the next 2 hours of the journey with the speed of 25 miles per hour. Find its average speed.
Distance $=$ Speed $\times$ time
The distance traveled in the first 3 hours with the speed of 20 mph $= 20 \times 3 = 60$ miles
The distance traveled in the next 2 hours with the speed of 25 mph $= 25 \times 2 = 50$ miles
Total distance traveled $= 60 + 50 = 110$ miles
Total time taken $= 3 + 2 = 5$ hours
Average speed $= \frac{110}{5} = 22$ miles/hour
Facts about Average Speed Formula
- Average speed is a scalar quantity, which can only be represented by magnitude. It has no direction.
- Average speed is independent of the direction of travel; it only depends on the total distance and time.
- It is essential to differentiate average speed from average velocity. Average velocity is a vector quantity that considers both magnitude and direction.
Conclusion
The average speed formula is calculated by dividing the total distance covered by the total time taken. In this article, we explored the concept of average speed, its formulas with different cases, and examples. Let’s solve a few examples and practice problems based on these concepts.
Solved Examples on Average Speed Formula
1. John walks a distance of 5 miles in 2 hours. Calculate his average speed.
Solution:
Using the average speed formula, we get
Average speed $= \frac{Total \;Distance}{Total \;Time}$
Average speed $= \frac{5 \;miles}{2 \;hours}$
Average Speed $= 2.5$ miles/hour
2. A car travels at a speed of 24 miles/hr for 2 hours and then decides to slow down to 18 miles/hr for the next 2 hours. What is the average speed?
Solution:
Distance $=$ Speed $\times$ time
The distance traveled in the first 2 hours with the speed of 24 mph $= 24 \times 2 = 48$ miles
The distance traveled in the next 2 hours with the speed of 18 mph $= 18 \times 2 = 36$ miles
Total distance traveled $= 48 + 36 = 84$ miles
Total time taken$ = 2 + 2 = 4$ hours
Average speed $= \frac{84}{4} = 21$ miles/hour
3. Walter drives at a speed of 60 mph from his house to his office every day. He returns from work at the speed of 45 mph. What’s his average speed for the round trip?
Solution:
Walter travels the same distance (both ways) with different speeds. We will use the average speed formula for the round trip.
$x = 60$ mph speed with which Walter travels from home to office
$y = 45$ mph speed with which Walter travels back to home from office
Average speed $= \frac{2xy}{x + y} = \frac{2\times 60 \times45}{60 + 45} = \frac{210}{105} = 51.42$ miles/hour
Practice Problems for Average Speed
Average Speed Formula: Definition, Examples, Facts, FAQs
A kid walks a distance of 5 miles in 3 hours. What is the average speed?
To find the average speed, we divide the total distance covered (30 miles) by the total time (2 hours). Therefore, Average Speed $= \frac{5}{3} = 1.67$ mph.
A runner completes the first 1.5 hours of a race with the speed of 9 miles per hour and the next 1 hour with the speed of 10 miles per hour. What is the runner's average speed?
$D_{1} = 9 \times 1.5 = 13.5$ miles
$D_{2} = 10 \times 1 = 10$ miles
Total distance $= 23.5$ miles
Total time $= 2.5$ hours
Average Speed $= \frac{23.5\; miles}{2.5\; hours} = 9.4$ mph
If a car covers distances $D_{1},\; D_{2}$, and $D_{3}$ for time intervals $T_{1},\; T{_2}$, and $T_{3}$ respectively, the average speed is
If a car covers distances $D_{1},\; D_{2}$, and $D_{3}$ for time intervals $T_{1},\; T_{2}$, and $T_{3}$ respectively, the average speed is total distance divided by the total time.
Average speed $= \frac{D_{1} + D_{2} + D_{3}}{T_{1} + T_{2} + T_{3}}$
Frequently Asked Questions on Average Speed Formula
What is the average speed calculation formula?
Average Speed $=$ Total Distance / Total Time is the average speed equation.
What distinguishes average speed from average velocity?
While average velocity accounts for both magnitude and direction, average speed solely takes into consideration the amplitude of motion.
Can average speed be negative?
Average speed does not have direction and it can only be positive or zero.

















