What is a Bisect?
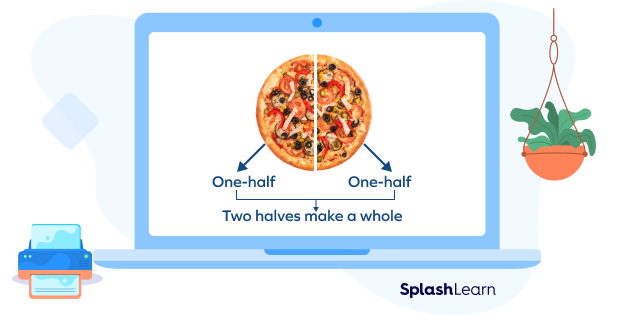
To bisect in geometry simply means dividing a shape into two equal parts. In life, we come across many situations, where we need to divide something equally among two parts. When an object is divided into two identical parts, each part is called a “half,” denoted as a fraction $\frac{1}{2}$.
For example, when we divide a pizza into two equal parts, it is called “bisection.”
Bisect: Definition
To understand the word bisect, we need to ask a question, what does bisect mean? The definition of “bisect” can be given as a mathematical process of dividing a geometrical figure into two parts of equal sizes.
We can bisect various objects, such as lines, angles, and other closed shapes. The term bisect in geometry is usually used when a line segment or an angle is divided into two equal parts.
For example, bisection of a line segment is defined as dividing the line segment into two line segments of equal lengths. Bisecting a closed shape means dividing it in two shapes of equal area.
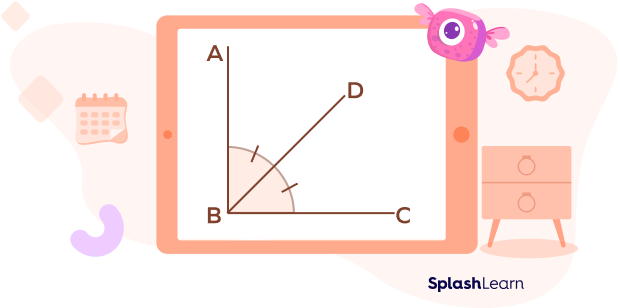
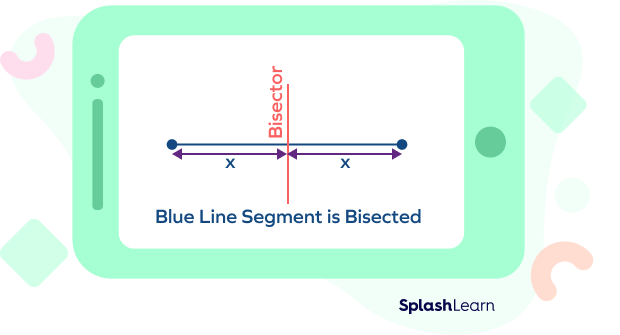
“Bisect” examples:
- Bisecting an angle
- Bisecting a segment
Bisecting a Line Segment: Steps of Construction
To bisect a line segment, we create circular arcs, on either side of the line segment, from both ends of the line segment, where these circular arcs meet on either side and are then marked and connected, intersecting the original line segment at a point that bisects it. Let’s understand it better with the proper steps of construction.
Step 1: Draw the line segment of the given length, say AB.
Step 2: Open a compass to the distance equal to roughly more than half of the length of AB.
Step 3: Cut two arcs on either side of the line segment AB, centered on A.
Step 4: Repeat step 3 but from B, make sure to keep the radius of the arcs the same as in step 3.
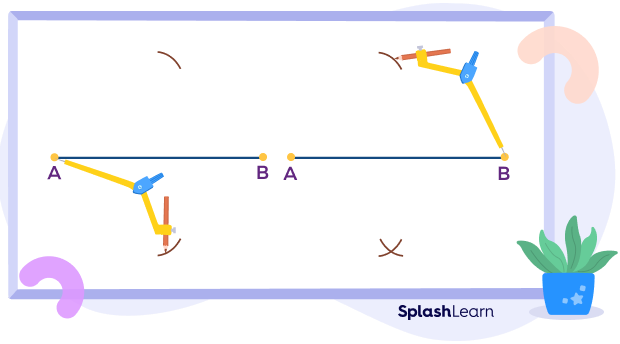
Step 5: Mark the points where the arcs meet on either side of the line segment, say P and Q respectively.
Step 6: Join PQ, and mark the point where PQ intersects AB as C.
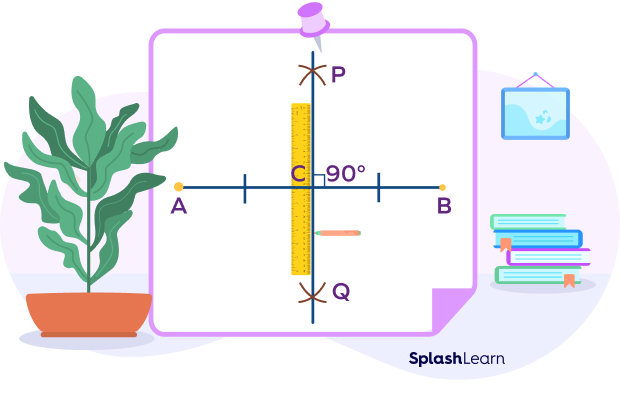
Step 7: AC and BC are bisections of the line segment AB.
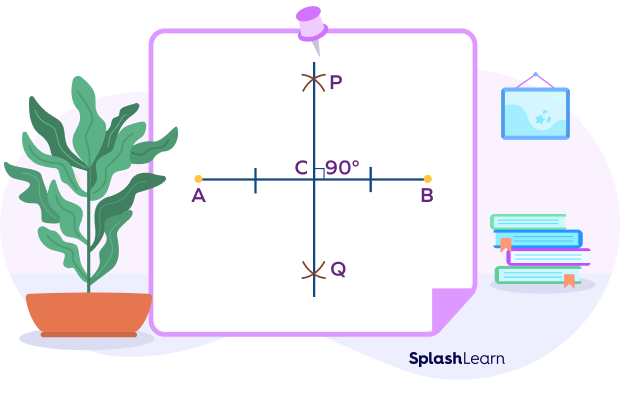
Note: The bisector formed here is a perpendicular bisector.
Bisecting an Angle: Steps of Construction
To bisect an angle means to draw a ray originating from the vertex of the angle in such a way that the angles formed on either side of this ray are equal to each other and half of the original angle. To achieve this, we draw an arc of arbitrary radius centered at the vertex of the angle, such that the arc bisects both the arms of the angle and then we mark these points. Now we draw two more arcs from these new points such that they intersect in front of the angle and we once again mark this intersection, and finally, if we join this point to the vertex of the angle, we have successfully bisected the angle. Let’s understand it better with the proper steps of construction.
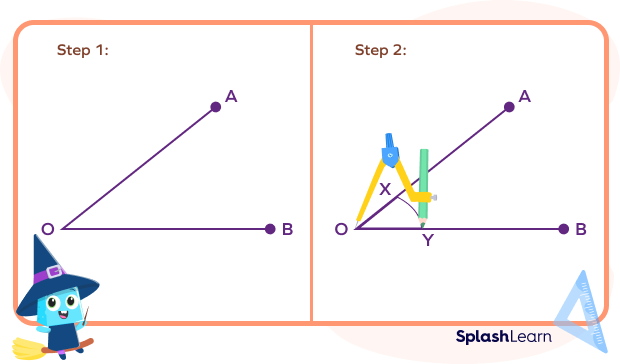
Step 1: Draw the given angle with the help of a protractor, say $\angle AOB$.
Step 2: Open a compass to a small radius, and cut an arc centered at O such that it intersects both arms of $\angle AOB$.
Step 3: Mark the intersections at both arms X and Y respectively.
Step 4: Cut two more arcs in front of $\angle AOB$ centered at X and Y each.
Mark the point where the arcs intersect as C.
Draw a ray originating at O passing through C.
$\angle AOC$ and $\angle BOC$ are the required bisections of $\angle AOB$.
The following image shows the steps for the construction of an angle bisector followed by a
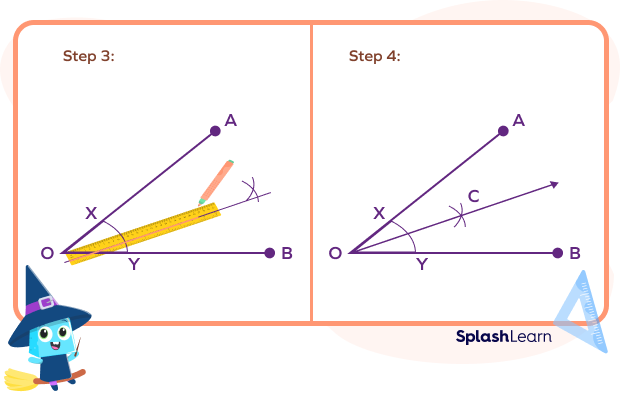
Bisecting a Shape
To bisect a shape, we need to divide the shape into two parts of equal area. For symmetric shapes, we can draw a line that divides the shape into two identical halves. Take a look at the following figure!
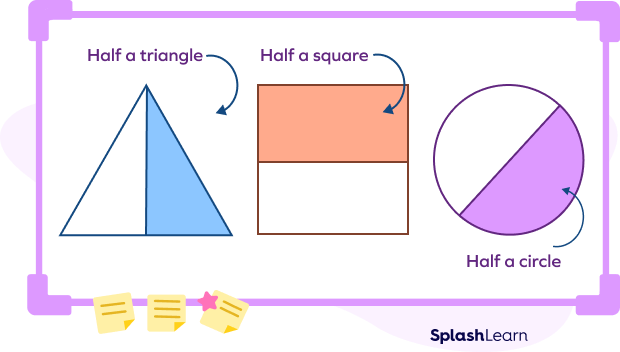
To bisect a symmetrical shape, we can simply cut it along a line of symmetry and the shape will be bisected into two shapes of equal area. These are known as trivial bisectors of symmetric shapes.
There are also some shapes that can be bisected by different lines other than lines of symmetry. These other lines are usually their medians.
Fun Facts!
- Bisect means to divide into two equal parts.
- We can mark any point on a line and it’ll be a bisector since a line can be extended infinitely long on either side. Hence, a line has infinite bisectors.
- A circle also has an infinite number of bisectors since it has an infinite number of lines of symmetry along each of its diameters.
Conclusion
In this article, we learned about the concept of bisection in geometry. Bisection means dividing a geometrical object into two equal parts. The equality of the two parts is defined differently for different objects, for line segments and curves it is defined as dividing it into two equal lengths, for angles its two equal angles, and for closed shapes, it’s two shapes of equal areas. We also learned the steps of construction for bisecting line segments and angles.
Solved Examples on Bisect
- In the following image if the m$\angle ABC = 80^{\circ}$. BD is an angle bisector of $\angle ABC$. BE is an angle bisector of angle ABD, then find the measure of angle ABE?
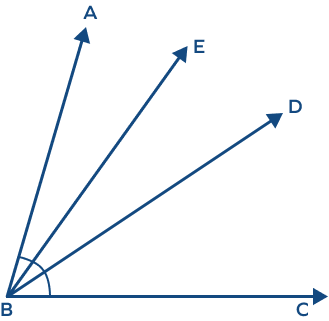
Solution: The angle bisector divides the angle into half.
BD is angle bisector of angle ABC.
$m\angle ABD = \frac{1}{2}m\angle ABC$
$\Rightarrow m\angle ABD = \frac{1}{2} \times 80 = 40^{\circ}$
Similarly, since BE is angle bisector of angle ABD, we have
$m\angle ABE = \frac{1}{2} mABD$
$\Rightarrow m\angle ABE = \frac{1}{2} \times 40$
$\Rightarrow m\angle ABE = 20^{\circ}$
- What is the value of x in the following image, if M is the midpoint of PQ?

Solution:
M is the midpoint of PQ.
$PM = MQ = \frac{1}{2} PQ$
$= \frac{1}{2} \times 24$
$= 12$ inches
Thus, x $=$ MQ $= 12$ inches
- A farmer has farmland of the isosceles trapezoid shape. He divides it equally between his two children. How much farmland will each child get?
[ Use: Area of trapezoid $= \frac{1}{2} \times (Sum\; of\; the\; parallel\; sides) \times Height$ ]
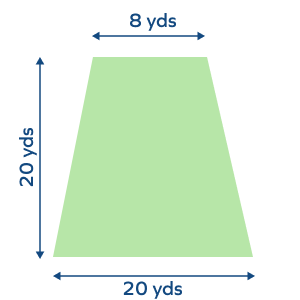
Solution:
In the image, we can see that the farmland is in the shape of an isosceles trapezium. The bisection can be done by drawing a bisector through the mid-points of the parallel sides since an isosceles trapezium is symmetrical along this line.
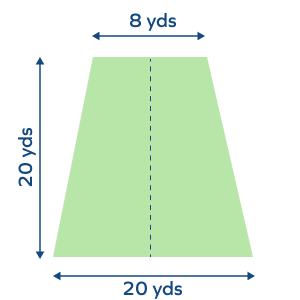
Area of the entire farmland $= \frac{1}{2} \times (Sum\; of\; the\; parallel\; sides) \times Height$,
Now, substituting the width of the farmland for the height of the trapezium, we have,
Area Area $= \frac{1}{2} \times (20 + 8) \times 20 = \frac{1}{2} \times 28 \times 20 =280\; yards^{2}$
The area of the farmland is 280 sq. yards.
After bisection, both children will get 140 sq. yards of the farmland.
Practice Problems on Bisect
Bisect: Definition, Formula, Examples
A point on a line segment equidistant from the endpoints of the same is called a __________.
A point at the exact middle of the line segment is the midpoint of the line segment.
How many trivial bisectors does a square have?
A square has 4 lines of symmetry. It has 4 trivial bisectors.
Find the measure of angle ABC, given that BD is the angle bisector.
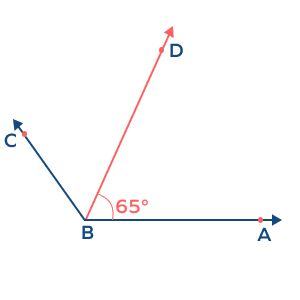
Angle bisectors divide the angle in two halves. The angle ABD is half of angle ABC, which means angle ABC is double of ABD. Thus, $m\angle ABC = 2 \times 65^{\circ} = 130^{\circ}$
Frequently Asked Questions on Bisect
What is a perpendicular bisector?
A perpendicular bisector is a line segment that is perpendicular to another line segment and also passes through the midpoint of the same.
Can a point be bisected?
A point has no dimensions, therefore, there is nothing to be divided into two equal parts in a point. Thus a point cannot be bisected.
Why is bisection important?
Bisection is an important part of geometry; many shapes and geometrical objects are drawn with the help of bisection, and we know that geometrical knowledge is important in architecture and some branches of engineering.
















