Center of Circle – Definition, Formula, Examples

What Is the Center of a Circle?

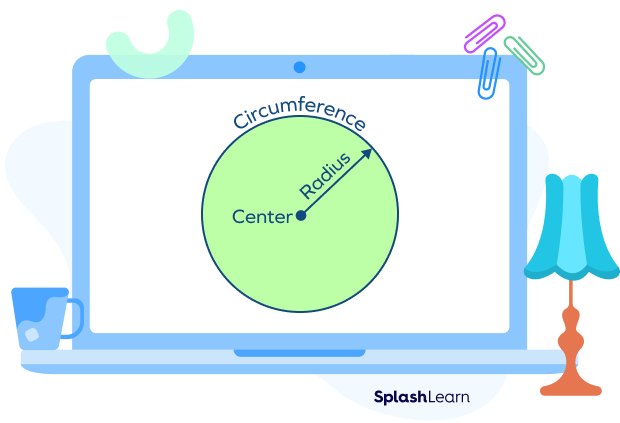
A circle is the set of all points (or locus of all points) in the plane that lie at a fixed distance from a fixed point. The fixed point is called the “center” of the circle. The fixed distance is called “radius.” 

Center of a Circle: Definition

A circle is a two-dimensional shape defined by its center and radius. We can draw any circle if we know the center and radius. A circle can have an infinite number of radii. The center point is the midpoint where all radii intersect. It can also be defined as the midpoint of the diameter of the circle.

We can construct a circle of any radius using a compass. The distance between the pencil and the pointer of a compass is adjustable. Construct the center of a circle by keeping the pointer on any fixed point.  Set the distance equal to the required radius. Draw a complete circle without changing this distance. The fixed point acts as the center of the circle.

Center of a Circle: Formula

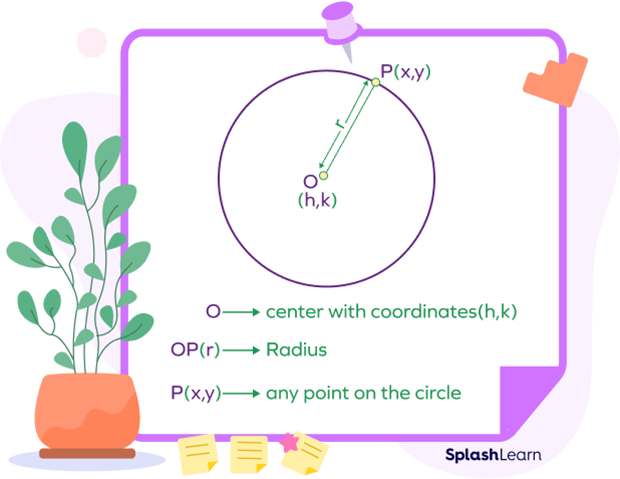
The formula for the center of a circle is also known as the general equation of a circle. If the coordinates of the center of the circle are (h,k), and r is the radius, and (x,y) is any point on the circle, the formula for the center of the circle is as follows:

$(x\;-\;h)^{2} + (y\;-\;k)^{2} = r^{2}$

This is also known as the equation of the center of a circle. We’ll use this formula in the

following sections to find the center of a circle, or the equation of a circle.

Equation of a Circle with Center at Origin

If the center of a circle lies at the origin (0,0) and radius is r units, then the equation of the circle is given by

$(x\;-\;0)^{2} + (y\;-\;0)^{2} = r^{2}$

$x^{2} + y^{2} = r^{2}$

How to Find the Center of a Circle

To find the center of the circle, we’ll consider two cases:

• We need to locate the center of the given circle.
• We need to find the coordinates of the center of the circle using the equation of the circle.

When a circle is given

When we’re given a circle and we need to find its center, we can follow the steps listed below:

Step 1: Draw a chord AB in the circle and note down its length carefully .

Step 2: Draw another chord CD parallel to AB so that it is the same length as AB.

Step 3: Use a ruler to connect points P and N with a line segment.

Step 4: Connect points B and C.

Step 5: The intersection of AD and BC is the center of the circle.

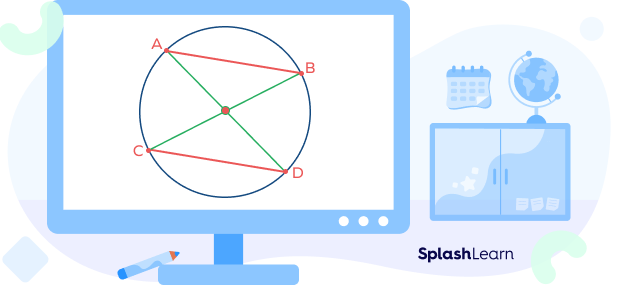
In a similar way, the center of a circle can be found using secants (chords are the part of secant inside the circle). Also, we can use the perpendiculars of tangents at the point of contact to find the center. All three of these follow the same principle that radius is perpendicular to them a certain point (midpoint for chord and secant and point of contact for tangents.

When the equation of a circle is given

Let’s understand how to find the center of a circle with an equation of the circle known to us.

Step 1: Write the given equation in the general equation form for a circle.

Step 2: Compare the equation with the general equation to determine the values ​​of h,k, and r.

For example: The equation of a circle is $x^{2} + y^{2}\;-\;4y = 0$.

It can be rewritten as

$x^{2} +(y^{2}\;-\;4y + 4)\;-\;4 = 0$ … complete the square

$(x\;-\;0)^{2} + (y\;-\;2)2 = 4 = 2^{2}$… since $(y\;-\;2)^2 = y^{2}\;-\;4y + 4$

Comparing with the general equation we have h $= 0$, k $= 2$ and r $= 2$. Thus the center of the circle is (0, 2).

When endpoints of a diameter are given

If the endpoints of the diameter are given, then to find the coordinates of the center

point, we use the midpoint formula, since the center is the midpoint of the

diameter. The steps to find the center of the two points are as follows:

Step 1: Assume that the circle’s center is at these coordinates $(h,k)$.

Step 2: If $(h, k)$ is the midpoint coordinates of a line segment with

endpoints $(x_{1},\;y_{1})$and $(x_{2},\;y_{2})$, then by midpoint formula we can write

$(h, k) = (\frac{x_{1}+ x_{2}}{2},\frac{y_{1} + y_{2}}{2})$

Step 3: Simplify to get the coordinates of the center of the circle.

Let’s take an example of a circle where the endpoints of the diameters are $( \;-2,\;4)$ and $4(6, \;16)$.

Then, its center coordinates are:

$(h,k) = (\frac{-2+6}{2},\frac{4+16}{2})$

$(h,k)=(\frac{4}{2},\frac{20}{2})$

$(h,k)=(2,\;10)$

Therefore, the coordinates of the center of the circle whose endpoint is the diameter are (2,10).

Fun Facts about the Center of a Circle

• If a circle is divided into two equal parts, each part is called a semicircle. The diameter of a circle divides it into 2 semicircles.
• A sector of a circle is part of a circle in between two radii and an arc; there is a unique sector, formed by radii at right angles and is known as a quadrant.
• The perpendicular bisectors of any two chords of a circle always meet at the center of a circle.

Conclusion

The center of a circle is a point inside the circle, which is equidistant from all the points on the boundary of the circle. In this article, we learned about the center of a circle, its properties, and how to find the center of a given circle using different methods.

Solved Examples on Center of a Circle

1. Find the equation of a circle, given the coordinates of the center are (3, 1), and the radius of the circle is 5 units. Check if the origin lies inside the circle, on the circle, or outside of the circle.

Solution:

The equation of the center of the circle is $(x \;–\; h)^{2} + (y \;–\; k)^{2} = r^{2}$. 

Center coordinates $(h, k)$ are $(3,4)$, radius r$=5$ units.

By substituting these values for h,k, and r in the equation, we have,

$(x\;-\;3)^{2} + (y\;-\;4)^{2} = 5^{2}$

On further simplification, we get

$x^{2} + y^{2} = 6x + 8y$,

Which is the equation for the given circle.

Now, if we put the values of $(x, y) = (0,0)$

We have,

$0^{2} + 0^{2} = 60 + 80$

$\Rightarrow 0 = 0$

Since LHS $=$ RHS, the point lies on the circle.

2. Consider a circle centered at the origin and having a radius equal to 8 units. Find its equation.

Solution:

Given: Center is (0,0) and radius is 8 units.

We know the equation of a circle with its center at the origin: $x^{2} + y^{2} = a^{2}$

For the given conditions, the equation of a circle is $x^{2} + y^{2} = 8^{2}$

$x^{2} + y^{2} = 64$, which is the equation of a circle

3. Find the equation of a circle with center (3,5) and radius 4 units.

Solution:

Here, the center of the circle is not the origin. So, the general equation for a circle is,

$(x\;-\;3)^{2} + (y\;-\;5)^{2} = 4^{2}$

$x^{2} \;–\; 6x + 9 + y^{2}\;-\; 10y + 25 = 16$

$x^{2} + y^{2}\;-\;6x\;-\;10y + 18 = 0$

4. The equation of a circle is $x^{2} + y^{2}\;−\;12x\;−\;16y + 19 = 0$. Find the center of the circle.

Solution:

The given equation is $x^{2} + y^{2}\;−\;12x\;−\;16y + 19 = 0$

We can rewrite it using completing the square.

Third term $= (Middle\; term/2)^{2}$

$x^{2}\;-\;12x + (\frac{12}{2})^{2} + y^{2} \;-\; 16y + (\frac{16}{2})^{2} =\;-\;19+(\frac{12}{2})^{2} +(\frac{16}{2})^{2}$

Simplifying,

$x^{2}\;-\;12x + 6^{2} + y^{2}\;-\; 16y + 8^{2} = \;-\;19 + 6^{2} + 8^{2}$

$(x\;-\;6)^{2} + (y\;-\;8)^{2} = \;-\; 19 + 36 + 64$

$(x\;-\;6)^{2} + (y\;-\;8)^{2} = 81$

Now comparing with the general equation, we have$(h,k) = (6,8)$

Practice Questions on Center of a Circle

Frequently Asked Questions on Center of a Circle