Circumference to Diameter: Conversion, Formula, Meaning, Example

What Is the Circumference to Diameter Calculator?

The circumference to diameter calculator is used to find the value of the diameter of a circle for a given value of circumference. To use the calculator, simply enter the measurement of the circumference and click on “Calculate” to get the result.

What is the circumference of a circle? Circumference is the total length of the boundary of the circle. The formula for finding the circumference of the circle is

$C = 2\pi r$ where r is the radius of the circle.

Diameter is a line segment through the center of a circle with its ends on the circle’s circumference. In the circle given below, AB is the diameter. Diameter is twice the radius.

$d = 2r$ where r stands for radius of the circle.

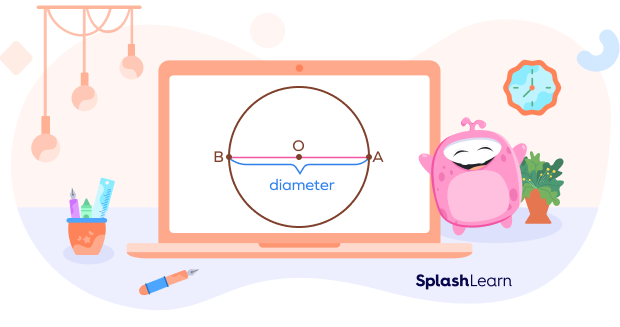
Thus, we can write $C = \pi d$

where, C is the circumference and d is the diameter.

To find the diameter, we can rewrite this equation as

$d = \frac{C}{\pi}$  

So, to find the value of the diameter from circumference, simply divide the circumference by $\pi$. 

Circumference to Diameter Ratio

Circumference to diameter ratio is the ratio that defines Pi $(\pi)$.

The radius, diameter, and circumference of a circle are all related through the mathematical constant $\pi$ (pi), which is the ratio of a circle’s circumference to its diameter. π is an irrational number. The value of π is approximately considered as 3.14159 or $\frac{22}{7}$.

Any two circles with different radii are similar as they have the same shape but different size. Thus, the ratio of a circumference of a circle to diameter is always constant for all circles. It never depends on the radius. This value is called pi $(\pi)$. It is an irrational number.

$C = 2\pi r = \pi d$

Thus, $\pi = \frac{C}{d}$

This formula also describes how to find the diameter of a circle with the circumference C. How can we find the diameter of a circle with the circumference C? Divide the circumference value by the number pi $(\pi)$, or use the formula $d = \frac{C}{\pi}$ .

When the circumference C is placed in a ratio with the diameter d, we get $\pi$.

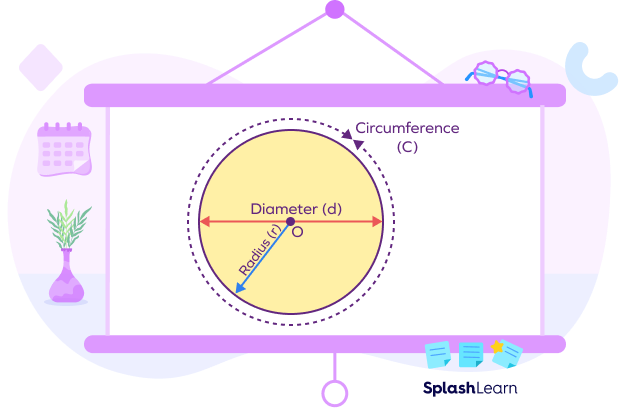
Circumference to Diameter Formula

We can find the circumference of a circle either by using the radius or the diameter of the circle. The following are the formulas for finding the circumference of the circle. 

Circumference of circle with radius: $C = 2\pi r$

Circumference of circle with diameter:  $C = \pi d$

where

• $C =$ Circumference
• $r =$ Radius
• $d =$ Diameter
• $\pi = \frac{22}{7}$or $3.14$ (approx)

Thus, the circumference to diameter formula, which is used to find diameter using circumference, can be given as

Circumference to diameter formula:  $d = 2r = \frac{C}{\pi}$

How to Find the Diameter from Circumference

To find diameter from circumference, simply substitute the value of the diameter in the formula $d = \frac{C}{\pi}$ .

Example: Find the diameter of a circle whose circumference is 6.28 inches.

Here, $C = 6.28$

$d = \frac{C}{\pi} = \frac{6.28}{3.14} = 2$ in

How to Find the Circumference from Diameter

To find circumference from diameter, simply substitute the value of the diameter in the formula C=πd.

Example: The diameter of the playground is 70 feet. Find its circumference.

Circumference of the playground $= C= \pi d$

$C = \frac{22}{7}\times70 = 220$ feet

How to Find the Circumference of the Circle When Area Is Given

Sometimes, we only know the area of a circle and we have to find the circumference. How to proceed in such cases? Consider an example.

Example: Area of a circular park is 6.16 square yards. What is the length of the boundary of the park?

Length of the boundary of circular park $=$ Circumference of the circle 

Area $= 6.16$ square yards

Area of a circle$ = \pi r^2$

$\frac{22}{7} \times r^2 = 6.16$

$r^2 = \frac{6.16 \times 7}{22} = 1.96$

$r = 1.4$ yards

$d = 2 \times 1.4 = 2.8$ yards

Circumference of the circular park $= \pi d = \frac{22}{7}\times2.8 = 8.8$ yards

Conclusion

In this article, we learned how to find the diameter of a circle using its circumference. We also explored the important formulas along with examples. Let’s look at some solved examples and practice problems to understand the concepts better.

Solved Examples on Circumference to Diameter

1. i) What is the circumference of the circle if the diameter is 1.4 inches? 

    ii) What is the diameter of a circle if its circumference is 1.4 inches?

Solution: 

i) Diameter $(d) = 1.4$ inches

   $C = \pi d$

   $C = \frac{22}{7}\times1.4$ 

   $C = 22\times0.2$

$C = 4.4$ inches

ii) Circumference $= C = 1.4$ inches

$d = \frac{C}{pi}$

$d = \frac{1.4}{3.14}$

$d = 0.4456$ in

2. Find the circumference of the circle if the radius is 2.75 inches (Use $\pi = 3.14$).

Solution: 

Radius $(r) = 2.75$ inches

Diameter $= 2r = 2\times2.75 = 5.5$ inches

$C = \pi d = 3.14\times5.5 = 17.27$ inches

3. What is the circumference of the circle if the area of the circle is is 38.5 square feet?

Solution: 

Area $= \pi r^2$

$38.5 = \frac{22}{7} \times r^2$

$r^2 = \frac{38.5\times7}{22} = 12.25$

$r = 3.5$ feet

Diameter $= 2r = 2\times3.5 = 7$ feet

$C = d = \frac{22}{7}\times7 = 22$ feet

4. Find the diameter of a circular garden with circumference 132 feet.

Solution: 

Circumference $(C) = 132$ feet

Diameter $(d) = \frac{C}{\pi}$

Diameter $(d) = \frac{132}{\pi}$

Diameter $(d)= \frac{132}{1} \times \frac{7}{22}$

Diameter $(d)= 42$ feet

5. The circumference of a circle is 33 inches. Find the diameter of the circle. 

Solution: 

$C = 33$ inches

$C = \pi d$

$33 = \frac{22}{7} \times d$

$d = \frac{33\times 7}{22} = 10.5$ inches

Practice Problems on Circumference to Diameter

Frequently Asked Questions on Circumference to Diameter