What Is a Coefficient in Math?
In mathematics, a coefficient is a numerical factor that accompanies a variable or term in an algebraic expression. Coefficients in algebraic expressions indicate the quantity by which the variable is multiplied or the term’s scale.
Examples of coefficients:
| Variable/ Expression | Coefficient |
|---|---|
| 3x2 | 3 |
| 2ab + 5c | 2, 5 |
| -6x2 + 2 | -6 |
Coefficients play a crucial role in simplifying equations, solving problems, and understanding the relationship between variables and their respective terms. Coefficient is a constant value that is multiplied by the variable of the same term is known as a Coefficient.
Coefficient example in math:
In the algebraic expression 5x + 2y + 7, ‘x’ and ‘y’ are the variables.
Since ‘5’ is multiplied by the variable ‘x’, 5 is the coefficient of x.
‘2’ is multiplied by the variable ‘y’, and 2 is the coefficient of y.
7 is the constant.
Thus, 5 and 2 are the coefficients in algebraic expression 5x + 2y + 7.
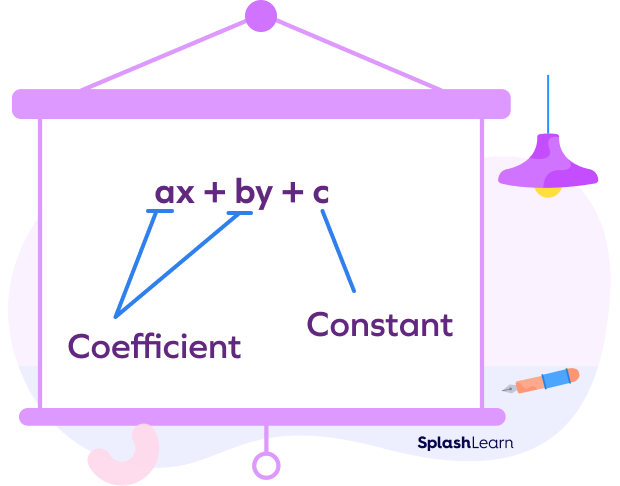
Coefficient: Definition
The coefficient is a numerical factor that multiplies a variable or term in an algebraic expression, indicating its scale or magnitude. It represents the specific quantity or value by which the variable is multiplied within the equation
A coefficient can be a positive or negative, decimal or fraction, real or imaginary or in any form. If the variables do not carry any coefficient, the coefficient will be considered 1.
Let us see more examples of Coefficients:
- -6 is the coefficient of the term -6x2 + 2
- 1 is the coefficient of the term xy + 7 Since there is no coefficient for the variable xy.
- 2 is the coefficient of x and -4 is the coefficient of y, in the term 2x-4y+50
Take a look at the picture to understand easily,

Coefficient of a Variable
The coefficient of a variable is an integer, any letter or symbol that is written with the variable or multiplied with it. The coefficient of a variable is the numerical factor that multiplies the variable in an algebraic expression. If the coefficient is not present, it is 1.
Example:
The coefficient of x in 5x is 5.
The coefficient of y in -y is -1.
Coefficient In An Expression
Coefficients in an expression are the numbers that accompany variables.
Example 1: 2x2 + 3x + 7 is an expression, which means it contains constant, variables and its coefficient with operators. In the expression, the 2x2 and 3x are the two terms with variables. Thus, the coefficient in the expression is 2 and 3.
Example 2: 2x2 + 4y + 3 = 0,
2 is the coefficient of the variable x2
4 is the coefficient of the variable y
3 is the constant
How to Find a Coefficient
To find the coefficient in an algebraic expression:
- Locate terms with variables and their powers.
- Ignore the variables and consider the numbers with which they are written or multiplied.
Example: In the expression 7x3 + 4x2 + y + 3 = 0:
The coefficient of x3 is 7.
The coefficient of x2 is 4.
The coefficient of y is 1 (since no number precedes y).
“3” is the constant term.
Numerical Coefficient
Numerical coefficients are the specific numbers or constants that accompany variables in algebraic expressions. Coefficient numbers represent the scale or magnitude by which the variables are multiplied. These coefficients can be positive or negative, whole numbers, decimals, fractions, real numbers, or even complex numbers. In essence, numerical coefficients provide essential information about the relative size or impact of the variables in the expression.
Example:
In 5y +10, the variable y has a numerical coefficient of 5.
In 6x + 2yz + 3, the numerical coefficients of x and yz are 6 and 2, respectively.
Leading Coefficient
The leading coefficient is the coefficient of the term with the highest degree in a polynomial expression.
When a polynomial is written in the standard form, and the first term is called the leading term and the coefficient of the first term is the leading coefficient. The coefficient of the term with the highest exponent or power in the polynomial equation is called the leading coefficient. The following figure will add further clarity to your understanding
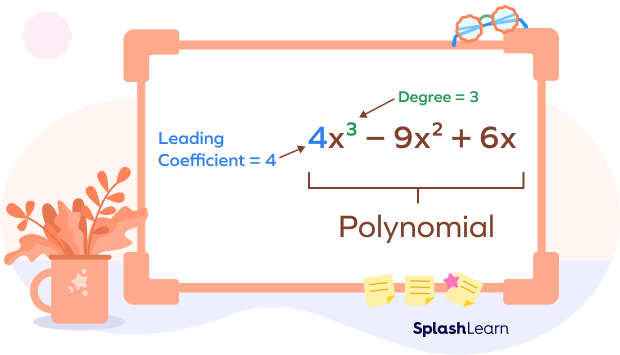
Here are some examples of leading coefficient in equations:
- In 4p2 + 3p + 7, the term with the highest exponent is 4p2 and the leading coefficient is 4.
- In 7 xy – 5x + 4, the leading coefficient is 7.
- 6 – 27a3 + 5a2, the leading coefficient of given expression is -27.
Tips and Tricks on Finding Coefficient
While checking for coefficient, remember the following points:
- A coefficient will always stick with the variable of the term or expression.
- If the variable does not have any number or symbol, then the coefficient of the variable is 1.
- ‘0’ can not be used as a coefficient of the variable.
Facts on Coefficient
- The coefficient is the constant number multiplied to the variable.
- In quadratic equations, the coefficient of the x2 term influences the shape of the parabola.
- In polynomial expressions, the leading coefficient is the one with the highest degree term.
- Zero coefficients result in terms being eliminated from the equation, simplifying it further.
Conclusion
In this article, we learned about coefficients in algebra, which are crucial numerical factors accompanying variables in expressions. They determine the scale and impact of variables in equations, leading to various mathematical implications. Let’s now deepen our understanding by solving examples and practicing MCQs for better comprehension.
Solved Examples on Coefficient
Example 1: From the given expression, identify the coefficient: 5x + 6y – 9
Solution:
The terms with variables in the expression are 5x and 6y.
The coefficient of variables x is 5.
The coefficient of y is 6.
Example 2: Determine the coefficient of x2 in the algebraic equation: 2 – 2y + 5x2
Solution:
Given equation: 2 – 2y + 5x2
5x2 is the term with variable x2 and coefficient 5.
Thus, 5 is the coefficient of x2 .
Example 3: Identify the leading coefficient: 15y2 + 19x – 4xy –5
Solution:
Given: 15y2 + 19x – 4xy – 5
Terms: 15y2, –4xy, 19, 5
Terms with Variables: 15y2, –4xy
Standard form: 15y2 – 4xy + 19x –5
The Leading coefficient is the coefficient of the term with the highest exponent or power.
15y2 is a term with the highest exponent.
So, 15 is the leading coefficient of the given expression.
Practice Problems on Coefficient
What is a Coefficient in Math? Definition, Facts, Examples, FAQs
What is the numerical coefficient of xy?
The term is xy. It has two variables.
There is no coefficient.
So, the coefficient is 1.
Identify the coefficients of the following algebraic expressions: $17x^{5} + 6y + 1$
The term with variables are $17x^{5},\; 6y$ and the coefficients are 17 and 6, respectively.
Which is the leading coefficient of the expression: $23a^{3} + 13a^{2} + 7a + 5 = 0$
Given expression: $23a^{3} + 13a^{2} + 7a + 5 = 0$
The term with highest exponent is 23a3. So the leading coefficient is 23.
Frequently Asked Questions on Coefficients
Can a coefficient be a negative value?
Yes. A coefficient can be a negative number or a symbol. For example, in the expression 3y-2x+7, the coefficient of x is -2.
Can a coefficient be zero?
No. A coefficient can not be zero because if 0 is multiplied by any variable or a term, the entire value of the term will be 0.
What is Constant value?
A constant value is a number that is fixed and can not be changed. For example in the expression, 5y + 9, 9 is the constant value.
What are polynomial coefficients?
Polynomial coefficients are the numerical values associated with each term in a polynomial expression.
















