What is the Common Difference of an Arithmetic Sequence?
An arithmetic sequence is a sequence of numbers in which the difference between two consecutive numbers is always constant. This difference is called a common difference of the arithmetic sequence.
For example, 1, 3, 5, 7, 9, … is an arithmetic sequence.
Here, the difference between any two consecutive terms is 2.
More examples of an arithmetic sequence are as follows:
0, 2, 4, 6, 8, 10, 12, …
4, 7, 10, 13, …
60, 55, 50, 45, 40, …
Common Difference: Definition
The common difference in arithmetic sequences is the difference between any two consecutive terms (difference between any term and its previous term) which is always constant. You can get the consecutive terms of an arithmetic sequence by adding the common difference to the previous term. It is usually denoted by “d.”
Let us understand the common difference in math and other terminologies in arithmetic sequence with an example. Imagine you want to buy a mountain bike that costs $\$150$. Your mother gave you an initial amount of $\$50$ to start your savings. Each month, you save $\$25$ from your pocket money to add to your savings. This can be represented as an arithmetic sequence as follows.
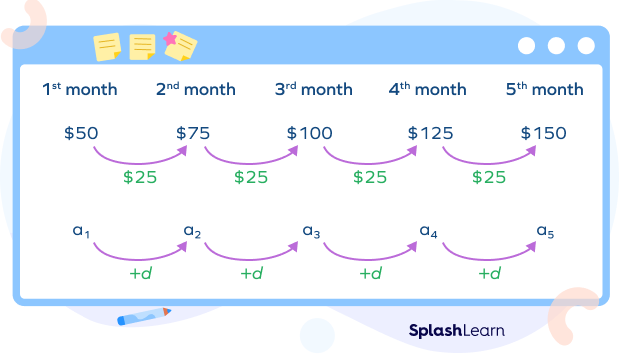
We can see that the sequence 50, 75, 100, 125, 150 is an arithmetic sequence with the common difference, $d = 25$.
Recommended Games
How to Find the Common Difference of an Arithmetic Sequence
For an arithmetic sequence $\left\{a_1, a_2, a_3, … a_{n-1}, a_n\right\}$, where n is the total number of terms in the sequence, the common difference “d” will be equal to the difference between any nth term and $(n-1)^{th}$ term, where n = 2, 3, 4, …, n.
$d = a_2\;-\;a_1 = a_3\;-\;a_2\; … = a_n\;-\;a_{n-1}$
For the sequence$ \left\{50, 75, 100, 125, 150\right\},\; d = 75\;-\;50 = 100\;-\;75 = 125\;-\;100 = 150\;-\;125 = 25$
Common Difference Formula
- When two consecutive terms in the sequence are given:
$d = a_n\;-\;a_{n-1}$, where an (the nth term) and $a_{n-1}$ (the previous term) are consecutive terms in the sequence.
- When the first and the last terms of the arithmetic sequence and the total number of terms are given:
$d = \frac{a_n-a_1}{n-1}, where an is the last term of the sequence, $a_1$ is the first term in the sequence, and n is the total number of terms in the sequence.
Recommended Worksheets
Facts about Common Difference
- It is denoted by the letter d.
- It is positive in an increasing arithmetic sequence.
- It is negative in a decreasing arithmetic sequence.
- For a constant sequence, the common difference is 0.
Example: 3, 3, 3, 3, 3, …
Conclusion
The common difference in arithmetic sequences is the difference between their two consecutive terms. For an arithmetic sequence, it is always constant. It is denoted by the letter ‘d’. It can be negative, positive, or zero.
Learn more mathematical concepts on SplashLearn, the game-based learning platform equipped with interactive games and fun worksheets.
Solved Examples for Common Difference
1. Find the common difference of the sequence:
32, 26, 20, 14, …
Solution: We can find the common difference by subtracting each pair of consecutive terms.
$d = 26\;-\;32 = 20\;-\;26 = 14\;-\;20 = \;-6$
Therefore, the common difference of the given sequence is -6.
2. Find the common difference of the arithmetic sequence $-\;\frac{1}{2},\; \frac{3}{2},\; \frac{7}{2},\;\frac{11}{2},\; …$
Solution: We can find the common difference by subtracting each pair of consecutive terms.
$d = \frac{3}{2}\;-\;\bigg(\;-\;\frac{1}{2}\bigg) = \frac{3}{2} + \frac{1}{2} = \frac{4}{2} = 2$
Also,
$d = \frac{7}{2}\;-\;\frac{3}{2} = \frac{4}{2} = 2$
Therefore, the common difference of the sequence $\bigg\{-12,\; 32,\; 72,\;112,\; …\bigg\}$ is 2.
3. What will be the 15th term of an arithmetic progression, if the 13th term is 25 and the common difference is 1.5?
Solution: It is given that $a_13 = 25$ and $d = 1.5$.
We know that we can get the next term in an arithmetic sequence by adding the common difference to its previous term.
$a_14 = a_13 + d$
$a_15 = a_14 + d = a_13 + 2d$
Substituting the given values.
$a_15 = 25 + 2(1.5) = 28$
So, the 15th term of the given arithmetic sequence is 28.
4. In the arithmetic sequence $\left\{k + 8, k^2 , 3k\;-\;2, 5k\;−\;10, 2k\;-\;3\right\}$, if $k = 3$, then find the common difference.
Solution: We can find the common difference by subtracting each pair of consecutive terms. To find the terms in the arithmetic sequences, let’s substitute 3 for k.
Given sequence $= \left\{3 + 8, 3^2 ,\; 3 \times 3\;-\;2,\; 5 \times3\;−\;10,\; 2 \times3\;-\;3\right\}$
Given sequence $= \left\{11, 9, 7, 5, 3\right\}$
So, 11 is the first term of the sequence and 9 is the second term of the sequence.
The difference between the first two terms, $11\;-\;9 = 2$.
Therefore, the common difference of the given arithmetic sequence is 2.
5. What is the common difference in the following sequence?
$\left\{0.3,0.11,0.19,0.27,0.35\right\}$
Solution: We can find the common difference by subtracting each pair of consecutive terms.
$d = 0.11\;-\;0.3 = 0.19\;-\;0.11 = 0.27\;-\;0.19 = 0.35\;-\;0.27 = 0.8$
Therefore, 0.8 is the common difference of the sequence $\left\{0.3,0.11,0.19,0.27,0.35\right\}$.
Practice Problems on Common Difference
Common Difference: Definition with Examples
Find the option that does not contain the consecutive terms of an arithmetic sequence.
We need to find the difference between the consecutive terms. The option with the unequal difference between the terms is the correct choice.
For option A: $34\;-\;13 = 55\;-\;34 = 21$
For option B: $25\;-\;3 \neq 49\;-\;25$
For option C: $55\;-\;33 = 33\;-\;11 = 22$
For option D: $40\;-\;28 = 52\;-\;40 = 12$
So, the terms 3, 25, 49 are not the consecutive terms of an arithmetic sequence.
Which of the following will be the common difference of the arithmetic sequence containing 35 terms, if its first and last terms are 6 and 108, respectively?
It is given that $a_n = 108, \;a_1 = 6,$ and $n = 35$.
We know that when the first and the last terms of the arithmetic sequence and the total number of terms are given we use the following formula to find the common difference:
$d = \frac{a_n-a_1}{n-1}$
$d = \frac{108-6}{35-1} = \frac{102}{34} = 3$
Which of the following is the common difference in the shown arithmetic sequence? $\left\{18, 36, 54, 72,...\right\}$
We can find the common difference by subtracting each pair of consecutive terms.
$d = 36\;-\;18 = 54\;-\;36 = 72\;-\;54 = 18$
Therefore, the common difference of the sequence, $\left\{18, 36, 54, 72...\right\}$ is 18.
If all the terms of an arithmetic sequence are the same, then its common difference is ___________.
If the common difference is zero, all the terms in the sequence will be the same. It is a constant sequence.
Which of the following will be the 70th term of an arithmetic progression, If the 71st term is $-277$ and the common difference is 10?
It is given that $a_71 = -277$ and $d = 10$.
We can get the previous term in an arithmetic sequence by subtracting the common difference from its next term.
$a_70 = a_71\;-d$
$a_70 = -277\;-\;(10) = -287$
So, the 70th term of the given arithmetic sequence is $-287$.
Frequently Asked Questions on Common Difference
Is the common difference the same for all arithmetic sequences?
No, all arithmetic sequences do not have the same common difference. But the common difference for an arithmetic sequence is always constant.
Can the common difference for an arithmetic sequence be different?
No, the common difference for an arithmetic sequence is always constant. If the common difference is not constant in a sequence then it is not an arithmetic sequence.
What are some common difference examples?
Some common difference examples are:
For the arithmetic sequence {0, 2, 4, 6, 8, 10, 12}, the common difference is 2.
For the arithmetic sequence {4, 7, 10, 13, …}, the common difference is 3. For the arithmetic sequence {60, 55, 50, 45, 40, …}, the common difference is $-5$.
Can the common difference for an arithmetic sequence be a decimal or a fraction?
Yes, the common difference for an arithmetic sequence can be a decimal or a fraction. It can be any rational number.
Which letter represents the common difference of an arithmetic sequence?
The letter “d” represents the common difference of an arithmetic sequence.
Can the common difference be negative?
Yes. Common differences can also be negative.
Example: $6,\; 4,\; 2,\; 0,\; -2,\; -4,\’ -6,$ …Here, the common difference is $-2$.




































