Comparing Decimals – Definition, Solved Examples, Facts, FAQs

What Is Comparing Decimals?

Comparing decimals is slightly different than comparing integers due to the presence of the decimal point. A decimal number has two components, a whole number part and a fractional part, separated by a decimal point. For example, 25.67 is a decimal number.

The knowledge of comparing decimals is useful in our day-to-day life, such as comparing prices, calculating change, comparing rates, etc. 

Example: A chocolate bar costs $\$2.5$ and a candy costs $\$1.99$. Which one is cheaper? To answer this question, we need to compare the decimals 2.5 and 1.99. Which decimal is smaller? Since $1.99 \lt 2.5$, we can say that a candy is cheaper than a chocolate bar.

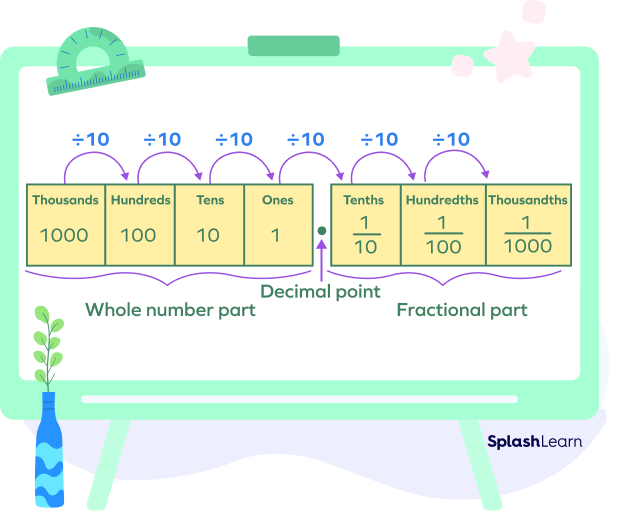
Every branch of mathematics makes use of the decimal numbers. Decimal numbers are really useful where precision is involved. Finding the larger and smaller decimal numbers in a given set of numbers is known as comparing decimals. Decimal numbers can be compared using the place value chart of decimals.

Take a look at the decimal place value chart.

How to Compare Decimals

To compare decimals, we begin by comparing the digits at the greatest place value. It is a common misconception that a decimal with more number of digits is greater. However, we must compare decimals using place values!

Comparing decimals is easier with the help of the place value chart. Write the decimals in the place value chart. If the digits at the highest place value match, move on to compare the digits at the next place value. We keep comparing digits this way until we reach different numbers.

Example: Consider the decimals 4.51 and 4.55.

One’s	Decimalpoint	Tenths	Hundredths
4	.	5	1
4	.	5	5

Here, the digits at ones place and tenths place are the same, so move to the hundredths place and compare numbers. 

As $1 \lt 5$, we can say that $4.51 \lt 4.75$

4.51 is less than 4.75.

What Are the Rules for Comparing Decimals?

Let’s understand this with steps. 

Step 1: Write the given decimal numbers in a place value chart. 

Once the place values of all the decimals are aligned, it is easy to compare them. If there are empty boxes at the end of the decimal, they can be filled with zeroes.

Step 2: Compare the whole number parts first. The decimal having the greater whole number part is greater!

Example: $24.11 \gt 21.99$ since $24 \gt 21$.

Step 3: If the whole number part is equal, we move on to the numbers in the next place value. 

Example: In 4.13 and 4.257, the whole number part, 4 is identical.

Comparing the digits at the tenth place, we get $1 \lt 2$.

At this step, we can conclude that the decimal $4.13 \lt 4.257$.

Comparing Decimals to the Hundredths Place

As we have seen, we compare decimal numbers by first comparing the whole number and then the digits that come after the decimal point. You will need to compare the decimals to the hundredths place if the digits up to the tenths place are identical.

Consider decimals 4.135 and 4.157. Let’s arrange them in the place value chart.

Ones	Decimal Point	Tenths	Hundredths	Thousandths
4	.	1	3	5
4	.	1	5	7

You can see that the digits up to the tenths place in both the decimals are the same. Thus, we compare the digits at the hundredths place.

$3 \lt 5$

Thus, $4.135 \lt 4.157$

Comparing Decimals and Fractions

To compare decimals and fractions, we convert the given fraction to a decimal number first, and then use the same rule of comparing decimals.

Consider an example. Let’s compare 1.261 and $\frac{5}{4}$.

Step 1: First, convert 54 into a decimal by dividing 5 by 4. 

 $\frac{5}{4} = 1.25$

Step 2: Compare 1.261 and 1.25.

Ones	Decimal Point	Tenths	Hundredths	Thousandths
1	.	2	6	1
1	.	2	5	0

• The whole number part 1 is identical.
• Moving to the next step, now the tenth place, 2 is also identical.
• Moving to the next step, the hundredth place is $6 \gt 5$. 

At this step, we can conclude that the decimal $1.261 \gt 1.25$. 

That implies $1.261 \gt \frac{5}{4}$.

Comparing Decimals on a Number Line

When comparing decimals on a number line, we use the basic rule of the number line, which states that the value of the numbers goes up as we move to the right. 

Let us understand comparing decimals on a number line using an example: 5.28 and 5.61. 

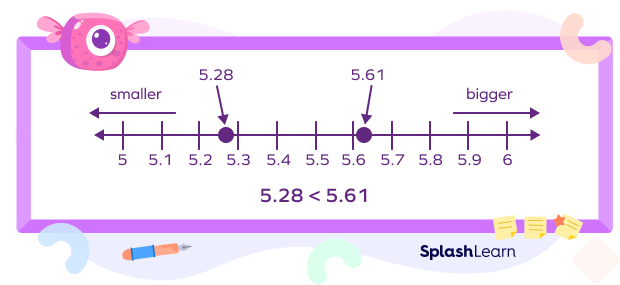
Step 1: First, locate the whole number part of decimals on the number line.

Since both of the given numbers are located between 5 and 6.

First, we mark the decimal numbers on the number line so that they include both numbers. 

Step 2: After that, we use a scale to mark all tenths decimal numbers between 5 and 6. Here, marking 5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 5.9, etc. 

Subsequent to denoting different tenths, we see that 5.28 comes between 5.2 and 5.3, and 5.61 comes between 5.6 and 5.7. 

Step 3: After representing both numbers on the number line we see that 5.61 is on the right side and 5.28 is on the left side. Hence, it follows that 5.28 is less than 5.61.

Ordering Decimals

To compare and order decimals, you first compare using the place value chart and then, you write them in a certain order (increasing or decreasing).

• Ascending order: Arrangement of decimals from least to greatest 
• Descending order: Arrangement of decimals from greatest to least

Example: Compare and write in descending order: 0.52, 1.21, 1.27, 2.25, 2.29

Ones	Decimal Point	Tenths	Hundredths
0	.	5	2
1	.	2	1
1	.	2	7
2	.	2	9
2	.	2	5

Here, $2.29 \gt 2.25$ (since ones and tenths are the same but at hundredth place $9 \gt 5$).

          $1.27 \gt 1.21$ (since ones and tenths are the same but at hundredth place $7 \gt 1$).

Also, comparing the whole number parts, we get 

$2 \gt 1 \gt 0$

So, we can put the given numbers in order as 

$2.29 \gt 2.25 \gt 1.27 \gt 1.21 \gt 0.52$

Facts about Comparing Decimals

Conclusion

In this article, we have learned how to compare decimals, rules for comparing decimals, and ordering of decimal numbers. Let’s solve a few examples for a better understanding.

Solved Examples on Comparing Decimals

1. Which decimal number is greater? 7.5 or 7.7?

Solution:

Given decimals are 7.5, and 7.7.

Here, the whole number part (7) is the same. 

Move on to compare the digits at the tenths place. We get $5 \lt 7$.

So, $7.5 \lt 7.7$.

Hence, 7.7 is greater than 7.5.

2. Compare the decimals 5.16 and 5.14.

Solution:

Given decimals are 5.16, 5.14.

Here, the whole number part (5) and tenth place digit (1) are the same. 

Comparing the digits at the hundredth place, we get 

$6 \gt 4$.

Hence, $5.16 \gt 5.14$.

3. Compare the decimal numbers 12.357 and 12.373.

Solution:

Given numbers are 12.357 and 12.373.

Here, the whole number part (12) and tenth place digit (3) are the same. 

At hundredth place, we have 

$5 \lt 7$

Hence, $12.357 \lt 12.373$.

4. Compare $\frac{5}{20}$ and 0.225.

Solution:

First, convert $\frac{5}{20}$ into a decimal. 

$\frac{5}{20} = \frac{1}{4} = 0.25$

Now, compare 0.25 and 0.225.

Here, the whole number part (0) and tenth place digit (2) are the same. 

At the hundredth place, we have

$5 \gt 2$

$\Rightarrow 0.25 \gt 0.225$.

Hence, $\frac{5}{20} \gt 0.225$.

5. Arrange the numbers 3.20, 5.52, 3.22, and 5.57 in ascending order.

Solution:

Ones	Decimal Point	Tenths	Hundredths
3	.	2	0
5	.	5	2
3	.	2	2
5	.	5	7

Comparing the whole number parts, we get 

$3 \lt 5$

Here, $5.57 \gt 5.52$ (since ones and tenths are the same but at the hundredth place $7 \gt 5$).

          $3.22 \gt 3.20$ (since ones and tenths are the same but at hundredth place $2 \gt 0$).

So, we can put the given numbers in the ascending order as

$3.20 \lt 3.22 \lt 5.52 \lt 5.57$

Practice Problems on Comparing Decimals

Frequently Asked Questions on Comparing Decimals