What Does Coplanar Mean in Geometry?
Coplanar simply means “lying on the same plane.” Here, “co” means “together,” and “planar” means “lying on a plane.”
In geometry, a plane is a two-dimensional, flat surface that extends infinitely in both dimensions.
When two or more points or lines lie on the same plane or common plane, they are said to be coplanar.
Now you might be wondering, what does non-coplanar mean? It is simply the opposite of coplanar and means “not lying on the same plane.”
Coplanar: Definition
Any geometric object or shape such as a line, point is said to be coplanar if they lie on the same plane. Otherwise, they are called non-coplanar.
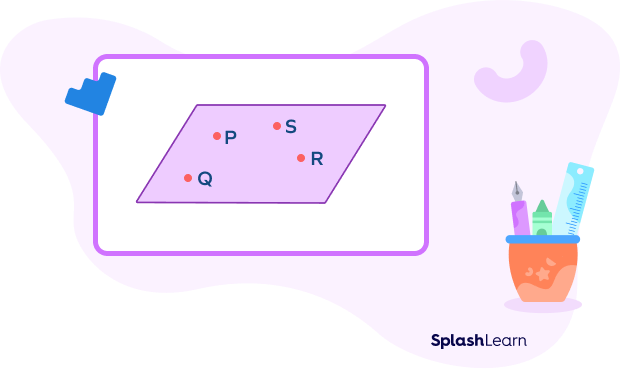
Example: Points P, Q, R, S lie in the same plane. So, they are coplanar.
What Is the Difference Between Collinear and Coplanar?
Collinear simply means lying on the same line. Coplanar means to exist on the same plane.
Collinear points lie on the same line. If points are collinear, they are also coplanar. However, coplanar points are not necessarily collinear.
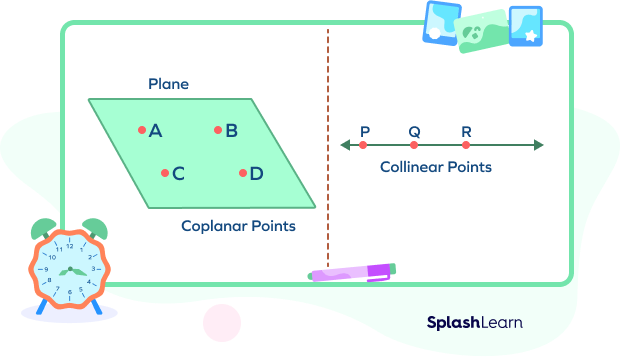
Here, the points A, B, C, and D are four coplanar points. However, they are not collinear. The points P, Q, R are collinear and thus also coplanar.
The concept of coplanar vs. non-coplanar points or coplanar vs. non-coplanar lines is quite intuitive. Let’s explore in detail.
What Are Coplanar and Non-coplanar Points?
Let’s understand the definition of coplanar points and non-coplanar points with examples.
Coplanar Points: Definition
Points that lie on the same plane are “coplanar points.”
Non-coplanar Points: Definition
Points that do not lie on the same plane are “non-coplanar points.”
Important Note:
We know that a line passes through any two given points. Thus, two points in a two-dimensional plane can always pass through a line and hence any two points are collinear (and thereby coplanar). Similarly, three points can always pass through a plane and hence any 3 points are always coplanar. Thus, we can say that four or more points that lie on the same plane are known as coplanar points.
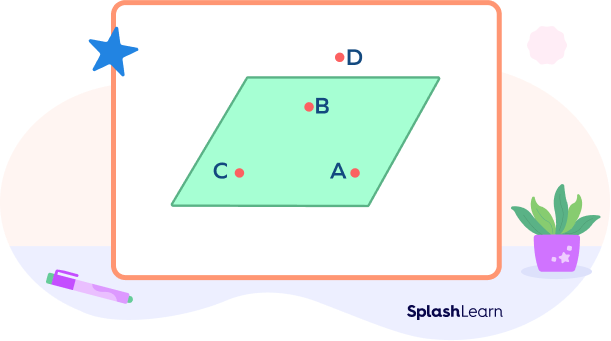
The points A, B, and C lie on the same plane.
They are coplanar.
Point D lies outside the plane.
It is not coplanar with the points A, B, and C.
However, if you choose any three points at random, they will be coplanar since a plane can be drawn through any three points.
By this logic, the points A, B, D are coplanar.
Points B, C, D are coplanar, and so on.
What Are Coplanar and Non-coplanar Lines in Geometry?
Let’s understand the definition of coplanar lines and non-coplanar lines using an example.
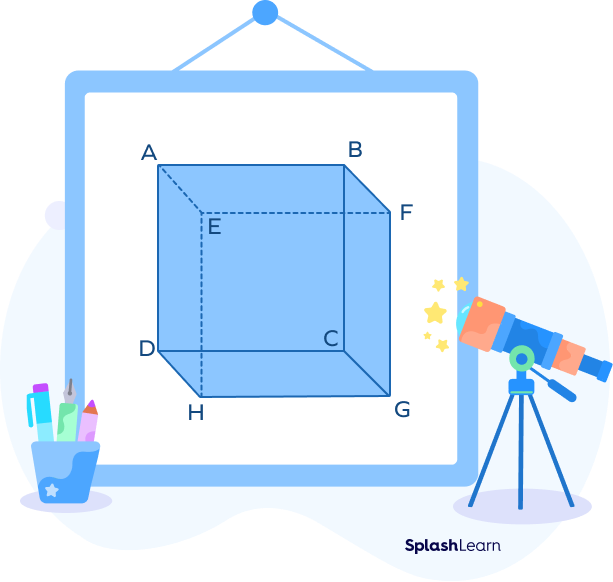
Coplanar Lines: Definition
When two or more than two lines lie on the same plane, those lines are said to be coplanar lines.
In the given cube, some examples of coplanar lines are as follows:
EF and GH are coplanar lines.
AD and DH are coplanar lines.
They reside on the same face of the cube.
Non-coplanar Lines Definition
When the lines do not lie on the same plane, they are called non-coplanar lines.
In the cube, some examples of non-coplanar lines are:
Lines AB, FG are non-coplanar.
Lines EF, CD are non-coplanar lines as they do not reside on the same face of the cube, i.e., not on the same plane.
Facts
- Any two points are always going to be coplanar.
- Any three points you take will always be coplanar.
- Four or more points are said to be coplanar if they are all present on one plane.
- Two lines whose one endpoint meet are coplanar by nature.
- Two parallel lines are always coplanar.
Conclusion
In this article we learned about collinear and coplanar points, their definition in geometry, coplanar and non-coplanar lines, methods to find if 4 points are coplanar or not, then we looked at how we can determine if two lines are coplanar.
Solved Examples on “Coplanar”
1. A point A, which has the coordinates $(3, \;-2, 4)$ lies on a plane surface having the equation $x \;-\; 4y + 2z\;-\;k = 0$. Find the value of k.
Solution:
Since A is coplanar or lies on the plane surface, it must satisfy the given equation.
To find k, put the coordinates in place of x, y and z.
$x \;-\;4y + 2z\;-\;k = 0$
$3\;-\;4(\;-2) + 2(4) \;-\;k = 0$
$3 + 8 + 8 \;-\; k = 0$
$19\;-\;k = 0$
$k = 19$
2. A set of points lie on the same line. Are they coplanar?
Solution:
A set of points lying on the same line are called collinear points. If points are collinear, they are also coplanar. Thus, the points are also coplanar.
3. Determine if coplanar or not: (i) Hands of an analog clock, (ii) Paint drops on a canvas.
Solution:
(i) The hands of an analog clock always lie and move on the same background plane of the clock, they are coplanar.
(ii) Paint drops can be considered points on a painting canvas, which is a 2D plane. So, they are coplanar points.
4. What do you mean by non-coplanar lines? Give a real world example.
Solution:
Non-coplanar lines are two or more lines which do not reside on the same geometrical plane. They are non-intersecting and do not satisfy the condition that the vector determinant should be zero.
One real world example of non-coplanar lines can be lines on the floor and lines on the wall of a room.
Practice Problems on “Coplanar”
Coplanar – Definition With Examples
The lines PQ and UV are _______.
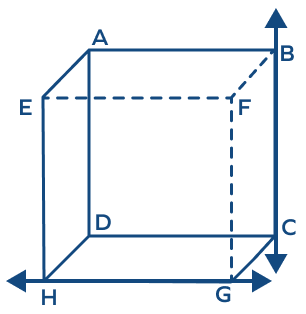
The lines do not lie on the same face of the cube. So, they are not coplanar.
Points A, F, B are _____

Points A, F, B are collinear and thus coplanar.
A point A which has the coordinates $(4, 5, \;-\;1)$ lies on the plane having the equation $2x\;-\;y + 5z\;-\;k = 0$. What is the value of k?
Since A is coplanar or exists on the plane surface, it must satisfy the given equation.
To find k, put the coordinates in place of x, y and z.
$2x \;-\; y + 5z \;-\; k = 0$ for A$(4, 5, \;-\;1)$
$2(4)\;-\;5 + 5 (\;-1)\;-\;k = 0$
$8\;-\;5\;-\;5\;-\;k = 0$
$\;-\;2 \;-\; k = 0$
$k = \;-\;2$
Any three points in a three-dimensional space are ____.
Any three points are always coplanar since you can have a plane passing through them.
Frequently Asked Questions on “Coplanar”
Are coplanar points also collinear?
Collinear points are always coplanar, but coplanar points need not be collinear.
Are collinear points also coplanar?
Yes, two or more collinear points are always coplanar. When there are multiple points residing on a line, and if we make a plane which goes through that line, the points will automatically reside on the plane, making them coplanar.
Give some examples of coplanar points.
Almost all the endpoints of a two-dimensional figure are coplanar. In three-dimensional form, the endpoints of one face of a cube can be considered coplanar.
Can the X and Y axes of the cartesian plane be considered coplanar?
Both axes intersect each other at right angles. So, these axes can be considered coplanar.
















