Comparing Numbers – Definition With Examples

What Does Compare Mean in Math?

The dictionary meaning of compare is to view something in relation to another. Comparing numbers in math is defined as a process or method in which one can determine whether a number is smaller, greater, or equal to another number according to their values. 

The symbols used for comparing numbers are “$\gt$”, which means “greater than”; “$\lt$”, which means “less than”; and “=”, which means “equal to”.

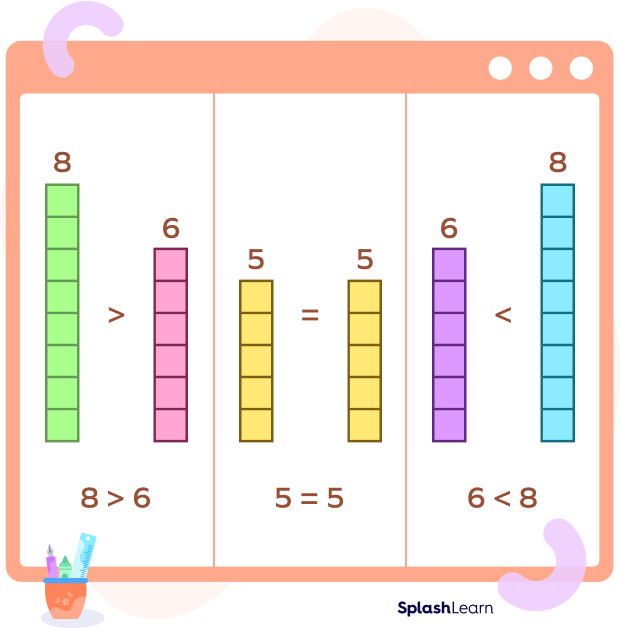
In the first part, 8 is greater than 6 as the purple blocks are two more than 6 green blocks. In the second part, $5 = 5$ as the numbers of orange blocks are the same in both the cases. In the third case, $6 \lt 8$ as there are 2 pink blocks less than 8 blue blocks. 

On comparison of two numbers, we can find out by how much a number is greater or smaller. 

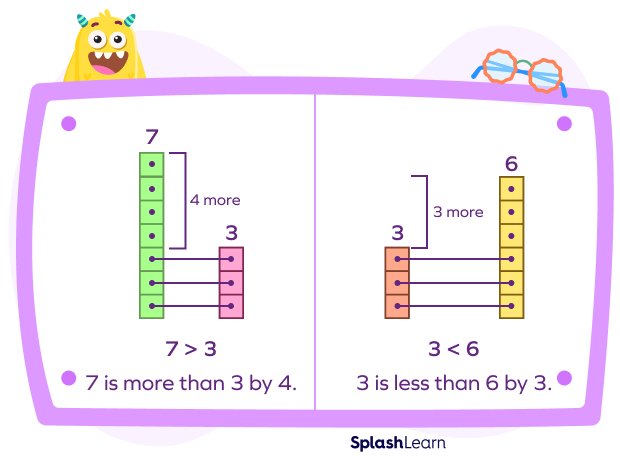
In the first part, we see that 7 is more or greater than 3 by 4. We can also say that $7 − 3 = 4$. In the second part, 3 is less or smaller than 6 by 3. We can also say that $6 − 3 = 3$. 

Comparing Numbers on a Number Line

Comparing the numbers on a number line is very easy. We just need to know the facts given below:

• For any two numbers marked on the number line, the number on the right side is greater.
• For any two numbers marked on the number line, the number on the left side is smaller.

For example: We have to compare $−6$ and 5.

We see that $−6$ is to the left of 5. So,$−6 \lt 5$.    

Comparing Whole Numbers

There are some steps through which we can compare two or more whole numbers:

Step 1: We should compare the number of digits. If there are more digits, it means the number is greater. 

Step 2: If the number of digits is the same in both the numbers, then we should compare the highest place values or the digit to the extreme left of the numbers.

Step 3: If the digits at the highest place value are the same, we should compare the digits in the next digits to the right or the second highest place value.

Step 4: We keep comparing digits with the same place value until we find digits that are different. The number with the greater face value is the greater number.

For example: We have to compare 5723 and 5800. 

The total number of digits in both numbers are the same. So, we move to the next step, i.e., to see if digits at highest place value are the same. Since the digit at the higher place value is the same, i.e., 5, we will look at the second highest place value. The second highest place value of 5800 is 8, whereas it is 7 for 5723. Hence, $5800 > 5732$. 

Difference $= 5800 − 5723 = 77$

Comparing Integers

• Comparing two positive integers is the same as comparing whole numbers. 
• A positive integer is always greater or more than the negative integer. 

For example, $2 \gt −3$ or $100 \gt −100$. 

• For comparing two negative numbers, we say that the greater number with a negative sign is the smallest of two negative integers.

For example, $−80 \lt −75$ or $−3 \lt −1$.

• Negative integers are less than 0 and positive integers are greater than 0.

For example, $−8 \lt 0$ or $3 \gt 0$. 

Comparing Fractions

Comparing Like Fractions

To compare two or more like fractions, we just have to compare the numerators. 

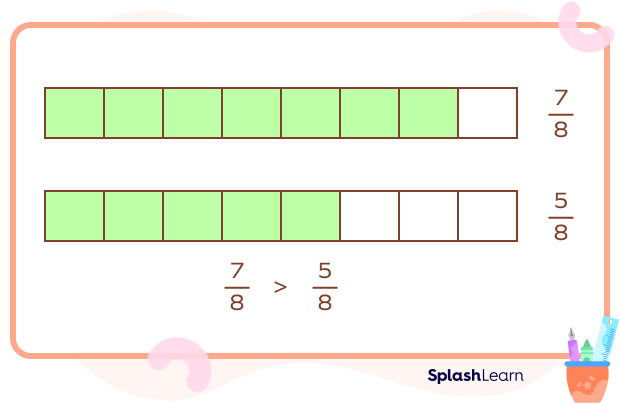
In the above image, since $7 \gt 5, \frac{7}{8}\gt\frac{5}{8}$. 

Comparing Unlike Fractions

To compare two or more unlike fractions, we can use different methods:

1. Cross Multiplication Method

We multiply the numerator of the first fraction by the denominator of the second fraction and write the answer.

For example, we have to compare $\frac{5}{8}$ and $\frac{6}{11}$.

So, we multiply 5 and 11 together and 8 and 6 together, we get

$5\times11=55$ and $8\times6=48$

After that, we can compare them like two whole numbers.

$55 \gt 48$

Finally, we replace the numbers by fractions. 

$\frac{5}{8} \gt\frac{6}{11}$

2. Making the Denominators the same 

In this method, we first find the LCM of both the denominators. 

Let us take the above example, i.e., compare $\frac{5}{8} $and$ \frac{6}{11}$.

LCM$(8, 11) = 88$

Multiply the numerator and denominator by the relevant numbers. 

$\frac{5\times11}{8\times11}=\frac{55}{88}$ and $\frac{6\times8}{11\times8}=\frac{48}{88}$

After the denominators become the same, we compare the numerator. $55 \gt 48$

Finally, we replace the numbers with fractions. 

$\frac{55}{88}\gt\frac{48}{88}\Rightarrow\frac{5}{8}\gt\frac{6}{11}$

Comparing Decimals

We can compare two or more decimals by using following steps:

Step 1: Firstly, compare the whole number part (i.e., compare the digits before the decimal). If they are different, you can compare the numbers as you would for any whole number. If they are the same, then follow the next step. 

Step 2: Compare the tenth place. If they are different, then compare the numbers as you would for whole numbers. If they match, then move on to the next digit.

Step 3: Compare the hundredths place. If they are different, then compare those digits as you would for whole numbers. If they match, then move on to the next digit. 

Example: Compare $23.56$ and $23.289$.

The numbers before the decimal are the same. So, we move to the next step, i.e., comparing the tenth place. Since $5 \gt 3, 23.56 \gt 23.289$. 

Comparing Rational Numbers

Comparing two or more rational numbers is similar to comparing fractions. We just need to keep in mind that:

• All negative rational numbers are smaller than 0.
• All positive rational numbers are more than 0.
• All positive rational numbers are more than all negative rational numbers.

Example: Compare$ -\frac{5}{6} $and$ -\frac{3}{4}$.

Let’s use the cross multiplication method.

$-5\times4=-20$ and $6\times -3= -18$

Since, $-20\lt -18$,

$-\frac{5}{6} \lt-\frac{3}{4}$

Comparing Numbers in Real Life

We can also compare distances between two places.

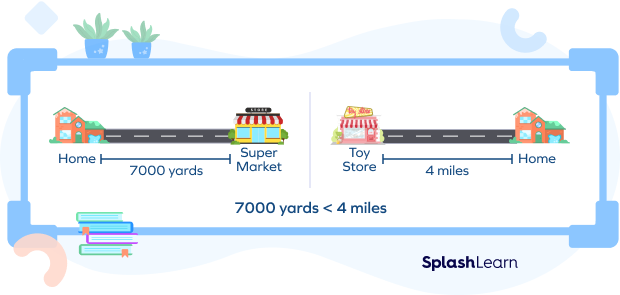
In the above image, 1 mile $= 1760$ yards

So, 4 miles $= 4 \times 1760 = 7040$ yards 

$7040$ yards $\gt$ $7000$ yards

We can also compare two quantities in terms of their weight.

In the above image, 1 pound $= 16$ ounces. 

So, 3 pounds $= 3 \times 16$ ounces

48 ounces $\gt$ 40 ounces 

We can also compare the capacity of the liquids. 

In the above image, $1$l $= 1000$ ml. 

So, $2$l $= 2 \times 1000$ ml

$2000$ ml$ \lt 2700$ ml.

Solved Examples

Example 1. Compare $−10$  and 5 on the number line. 

Solution: Let us draw a number line and mark $-10$ and 5 on it.

Since $−10$ lies on the left side of 5. 

So, $−10 \times 5$

Example 2. Which sign will come between $2\times750$ and $3\times550$? 

Solution: $2\times750=1500$

$3\times550=1650$

$1500\times1650$

Example 3. Compare $-\frac{5}{6}$ and $\frac{8}{9}$

Solution: Using cross multiplication method, we get 

$-5 \times 9 = -45$ and $6 \times 8= 48$

Since, $-45 \lt 48, -\frac{5}{6} \lt \frac{8}{9}$

Example 4. Compare $2$l $500$ ml and $3000$ ml.

Solution: $2$l $500$ ml $=2\times1000+500$ ml $=2500$ ml

$2500$ ml$\lt3000$ ml

$\Rightarrow2$l $500$ml$\lt3000$ml

Practice Problems

Frequently Asked Questions