What Is CPCTC in Geometry?
CPCTC in geometry simply stands for “Corresponding Parts of Congruent Triangles are Congruent.” CPCTC theorem states that if two or more triangles are congruent, then their corresponding angles and sides are congruent as well.
CPCTC: Definition
CPCTC meaning is “Corresponding Parts of Congruent Triangles are Congruent.” You can only use CPCTC after you know that two triangles are congruent. What is the CPCTC theorem?
The CPCTC theorem states that if two or more triangles are congruent to each other, then the corresponding angles and the sides of the triangles are also congruent to each other. Let us understand the meaning of congruent triangles and corresponding parts in detail.
Congruent Triangles
A triangle has three sides and three angles. The two triangles need to be of the same size and shape to be congruent. Both the triangles under consideration should superimpose on each other. For two triangles to be congruent, all 3 sides and angles should be congruent.
We also need to remember that when we state that two triangles are congruent, we name them such that the letters for corresponding vertices are in the same order. Take a look at the image given below:
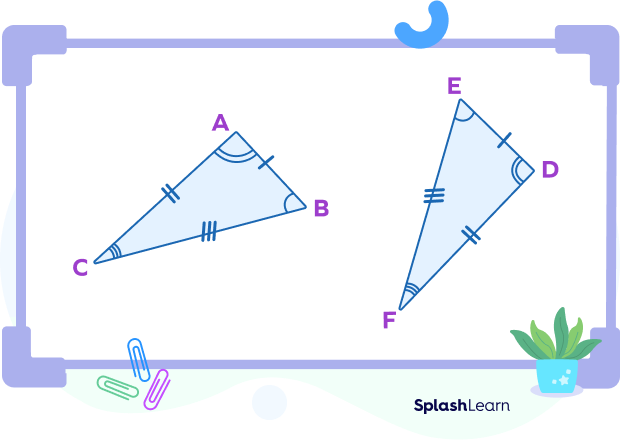
In the figure above, we see that the letters A, B, and C for the vertices of ABC correspond to the letters D, E, and F for the vertices of DEF respectively. We can state the congruences of sides and angles.
Side congruences: $\overline{AB} \cong \overline{DE},\; \overline{BC} \cong \overline{EF},\; \overline{AC} \cong \overline{DF}$
Angle congruences: $\angle ABC \cong \angle QRP,\; \angle BCA \cong \angle RPQ,\; \angle CAB \cong \angle PQR$
Now, we name the congruent triangles so that the letters for corresponding vertices match up in the triangle congruence statement.
$\Delta ABC \cong \Delta DEF$
Corresponding Parts
The corresponding parts of two triangles refer to the parts of two triangles that are in the same relative position. When a triangle’s three sides correspond to those of another triangle, they are at the same location or space. Corresponding angles signify that the three angles of one triangle are located in the same area as those of the other triangle. Take a look at the figure given below.
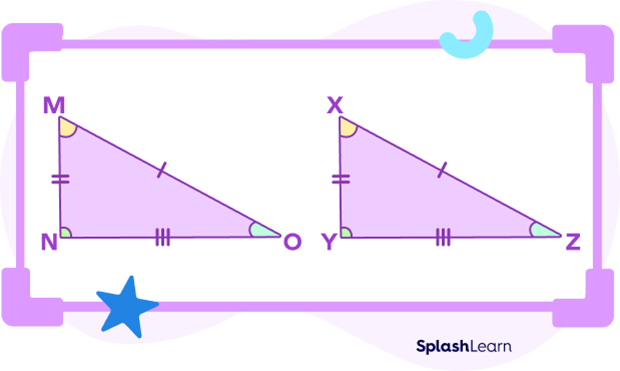
Here, $\Delta MNO \cong \Delta XYZ$. It means that the 3 pairs of sides and 3 pairs of angles of $\Delta MNO$ are congruent to the 3 pairs of corresponding sides and 3 pairs of corresponding angles of $\Delta XYZ$.
Now, let’s identify the 3 corresponding sides and the 3 corresponding angles:
MN corresponds to XY; NO corresponds to YZ; MO corresponds to XZ.
$\angle M$ corresponds to $\angle X;\; \angle N$ corresponds to $\angle Y;\; \angle O$ corresponds to $\angle Z$.
Since $\Delta MNO \cong \Delta XYZ$, as per the CPCTC theorem, the corresponding sides and angles are equal, which means,
$MN = XY,\; NO = YZ,\; MO = XZ,$ and
$\angle M = \angle X,\; \angle N = \angle Y,\; \angle O = \angle Z$.
CPCTC Triangle Congruence
According to the CPCTC, all of the corresponding sides and angles are congruent when two triangles are congruent by any criteria. Here, we’ll talk about five triangle congruence criteria or postulates.
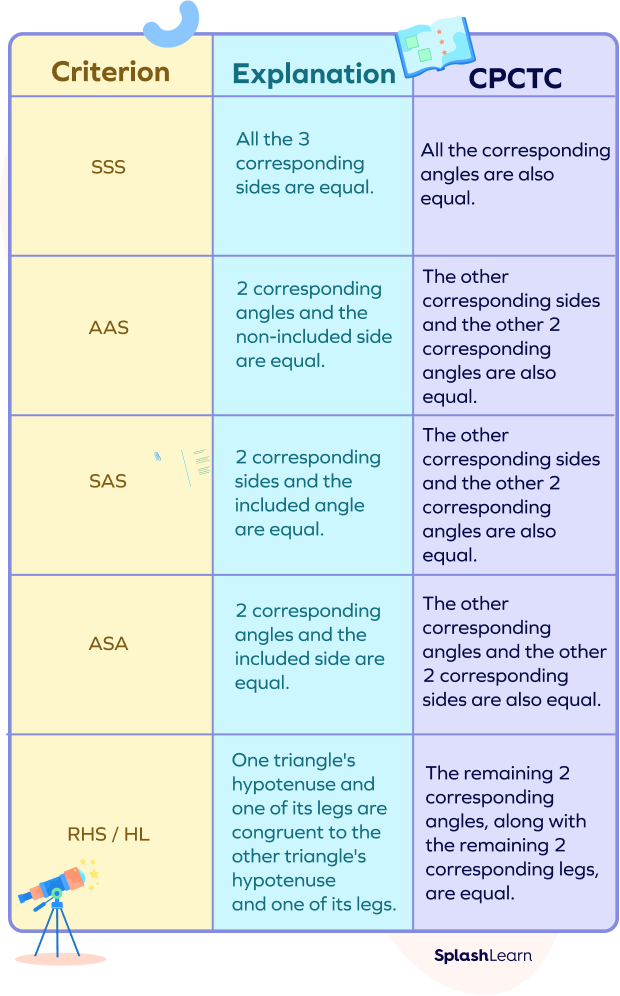
Visually, we can represent the rules as follows:
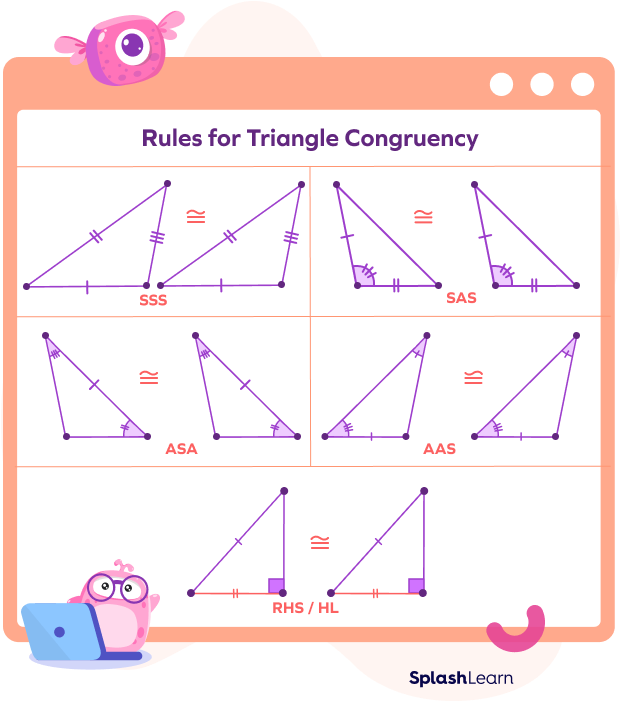
CPCTC Proof
Once it is shown that two triangles are congruent using one of the above congruence methods, we also know that all corresponding parts of the congruent triangles are congruent (abbreviated CPCTC).
Let’s consider an example:
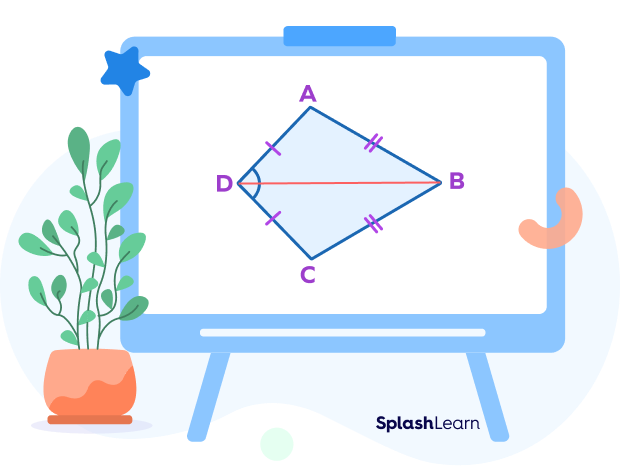
Consider $\Delta DAB$ and $\Delta DCB$ in which $BA = BC$ and $AD = DC$ are given.
Now, let’s prove the CPCTC theorem.
$BA = BC$ (Given)
$AD = DC$ (Given)
$BD = BD$ (Reflexive Property)
Thus, $Delta DAB \cong DCB$ by SSS criteria (Side-Side-Side)
Since the two triangles are congruent, we can use the CPCTC property and write
$\angle DAB \cong \angle DCB,\; \angle ADB \cong \angle CDB$ and $\angle ABD \cong \angle CBD$
Fun Facts!
- There are five conditions to determine if two triangles are congruent. They are
SSS, AAS, SAS, ASA, and HL criteria.
- SSS, AAS, SAS, ASA, HL use corresponding parts to prove triangles congruent, while CPCTC uses congruent triangles to prove corresponding parts congruent.
- By CPCTC, if two triangles are congruent, then you know that all pairs of corresponding sides are congruent and all pairs of corresponding angles are congruent.
- We use the symbol $“\cong”$ to denote congruence.
- If you know the two triangles are congruent, you need to match up the letters for their corresponding vertices, and then use those to state the congruences of angles and sides.
Conclusion
In this article, we learned in detail about the CPCTC definition, theorem, and proof. Let’s solve some examples and practice problems for better understanding.
Solved Examples on CPCTC
Example 1: Given $\overline{YX} \cong \overline{YZ},\; \angle XYW \cong \angle ZYW$, prove that $\overline{XW} \cong \overline{ZW}$.
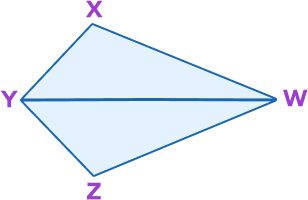
$YX \cong YZ$ (Given)
$\angle XYW \cong \angle ZYW$ (Given)
$WY \cong WY$ (Reflexive property)
Thus, $\Delta WXY \cong \Delta WZY$ by SAS criteria (Side-Angle-Side)
Thus, $XW \cong ZW$ (by CPCTC)
Example 2: Given: $\angle A \cong \angle C$, BY bisects $\angle ABC$. Prove that $\overline{AB} \cong \overline{CB}$.
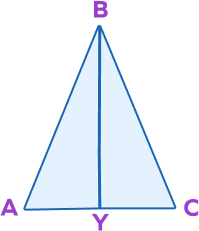
Solution:
$\angle A \cong \angle C$ (Given)
BY bisects $\angle ABC$ (Given)
$\angle ABY \cong \angle CBY$ (Definition of angle Bisector)
$BY \cong BY$ (Reflexive property/common side)
$\Delta AYB \cong \Delta CYB$ by AAS criteria (Angle-Angle-Side)
Thus, $\overline{AB} \cong \overline{CB}$ (CPCTC)
Example 3: Observe the figure given below and find the measure of $\angle I$ and length of $\overline{VU}$ using the CPCTC theorem, if $\Delta HJI \cong \Delta TVU$.
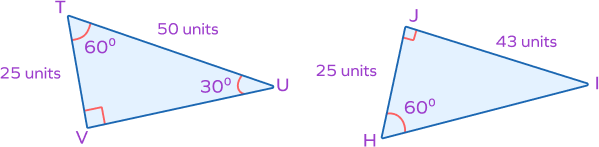
Solution: Given that $\Delta HJI \cong \Delta TVU$.
By applying the CPCTC theorem,
$\overline{HJ} = \overline{TV} = 25\; mm$
$\angle HJI \cong \angle VTU$
$\overline{HI} \cong \overline{TU} = 50\; mm$.
We can identify that $\overline{JI}$ and $\overline{VU}$ are the corresponding sides of two congruent triangles $\Delta HJI$ and $\Delta TVU$.
Therefore, $\overline{JI} = \overline{VU} = 43$ units
Thus, the length of $\overline{VU}$ is 43 units.
Also, by the same theorem, $\angle I = \angle U$.
Thus, $\angle I = 30^{\circ}$
Example 4: Observe the figure given below, in which $AC = CD$ and BC is perpendicular to AD. Find y by using the CPCTC theorem.
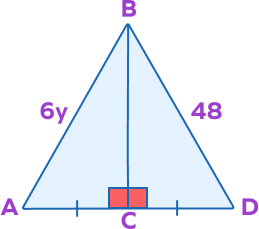
Solution: First let us prove that $\Delta ABC \cong \Delta BCD$,
$AC = CD$ (given)
$BC = BC$ (common side)
$\angle BCA = \angle BCD$ (as BC is perpendicular to AD)
Thus, $\Delta ABC \cong \Delta BCD$ (SAS criterion)
$AB = BD$ ( By CPCTC)
Now as $AB = BD$
Thus, $6y = 48$
$y = 8$ units
Example 5: Observe the figure given below in which $\angle PQR = \angle STU$ and $\angle PRQ = \angle SUT$, $\overline{QR} = \overline{TU}$. Find the value of x and y by using the CPCTC theorem.
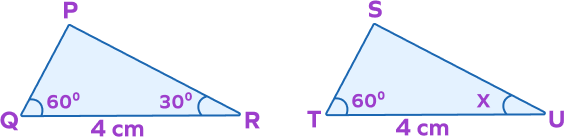
Solution: $\angle PQR = \angle STU$ (Given)
$\angle PRQ = \angle SUT$ (Given)
$\overline{QR} = \overline{TU}$ (Given)
Thus, $\Delta RPQ \cong \Delta UST$ (ASA criterion)
As $\angle R = \angle U$, we get $x = 30^{\circ}$
The value of $x = 30^{\circ}$
As we know, sum of three angles $= 180^{\circ}$
$\angle R + \angle P + \angle Q = 180^{\circ}$
$30^{\circ} + \angle P + 60^{\circ} = 180^{\circ}$
Thus, $\angle P = 180 \;-\; 90 = 90^{\circ}$
Now, by CPCTC, we know $\angle P = \angle S$
Thus, $\angle S = y = 90^{\circ}$
The value of $y = 90^{\circ}$
Practice Problems on CPCTC
CPCTC: Definition, Postulates, Theorem, Proof, Examples
What does CPCTC in math stand for?
CPCTC stands for Corresponding Parts of Congruent Triangles are Congruent.
If two triangles are congruent,it means that all of its corresponding _________ and _________ are congruent.
If two triangles are congruent, then all pairs of corresponding sides are congruent and all pairs of corresponding angles are congruent.
CPCTC theorem is used only when two triangles are ___.
CPCTC is used only when two triangles are congruent.
Which criteria proves these two triangles congruent?
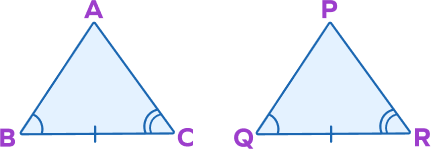
ASA is angle-side-angle. Given that, two corresponding angles and the included side are equal, the remaining corresponding angles and the other 2 corresponding sides are also equal by CPCTC.
What additional information is required for the 2 triangles to be congruent by ASA?
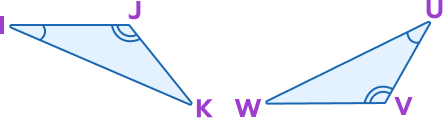
ASA is angle-side-angle.If any two angles and the side included between the angles of one triangle are equal to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.
Frequently Asked Questions on CPCTC
What is reflexive property?
The reflexive property states that any line segment or angle or shape is congruent to itself.
What must be proven before using CPCTC?
To prove CPCTC, we first prove the triangles congruent using SSS, AAS, SAS, ASA, or HL. Next, we can use CPCTC, which states that the other parts of the triangle are also congruent.
When and why is CPCTC used?
CPCTC is commonly used at or near the end of a proof, which asks the student to show that the two sides or angles are congruent. It is frequently used to assess the similarity and congruence of two or more triangles.
What is the third angle theorem?
If two angles in one triangle are congruent to two angles in another triangle, then the third pair of angles must also be congruent. This is called the third angle theorem.
Is CPCTC true for similar triangles?
In similar triangles, corresponding angles are equal, whereas corresponding sides of the triangles are not equal but proportional. So, we cannot apply the CPCTC theorem for similar triangles.
















