- What Is the Decimal Representation of Rational Numbers?
- Writing Rational Numbers in the Decimal Form
- Decimal Form of a Rational Number Chart
- Solved Examples on Decimal Representation of Rational Numbers
- Practice Problems on Decimal Representation of Rational Numbers
- Frequently Asked Questions on Decimal Representation of Rational Numbers
What Is the Decimal Representation of Rational Numbers?
Decimal representation of rational numbers is a method of finding decimal expansion of the given rational number or converting a rational number into an equivalent decimal number using long division.
Decimal form of a rational number example: $\frac{5}{4} = 5\div4= 1.25$
Rational numbers are the numbers of the form $\frac{p}{q}$, where p and q are integers and $q\neq0$. Decimals are the numbers that have a whole number part and a fractional part separated by a decimal point. Every rational number is either a terminating or repeating decimal.
Recommended Games
Writing Rational Numbers in the Decimal Form
To convert the rational number $\frac{p}{q}$ into a decimal, we divide the number p by the number q using the long division process. Writing rational numbers in decimal form involves two cases. The decimal form of a rational number we get can be of 2 types:
- When Remainder $= 0$, the decimal expansion is terminating.
Terminating decimal is the decimal number in which there is an end-digit. There are a finite number of digits after the decimal point.
For example, if we divide 5 by 1, we get 0.2. The number terminates and doesn’t continue after 2. So, it’s a terminating number.
- When Remainder $\neq0$, the decimal expansion is non-terminating and repeating.
In a non-terminating and repeating decimal, a single digit or a block of digits repeat themselves infinitely after the decimal point.
For example, we get $0.\overline{09}=0.09090909$ … on dividing 1 by 11. Here, the group of digits, 09, keep on repeating.
So, how are rational numbers written as decimals? Let’s discuss both the cases.
Recommended Worksheets
Terminating Decimal Representation of Rational Numbers
When the decimal expansion of $\frac{p}{q}$, $q\neq 0$ comes to an end after a finite number of digits, the decimal expansion is called terminating. In this case, when we divide p by q using the long division method, we get remainder 0.
Example 1: Find the decimal representation of the rational number $\frac{4}{5}$ .

Thus, $\frac{4}{5} = 0.8$ … terminating decimal expansion
Example 2: Find the decimal representation of the rational number $\frac{3}{4}$.
Here, $\frac{3}{4} = 0.75$ … terminating decimal expansion
Non-terminating and Repeating Decimal Representation of Rational Numbers
In some cases, when we divide p by q to find the decimal expansion of $\frac{p}{q}$, $q\neq 0$, the remainder never becomes 0. Also, the remainder repeats after some steps, which results in a non-terminating and recurring decimal expansion.
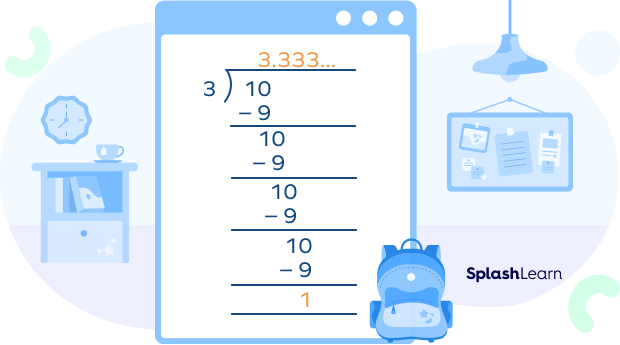
Example 1: $\frac{10}{3} = 3.333$…
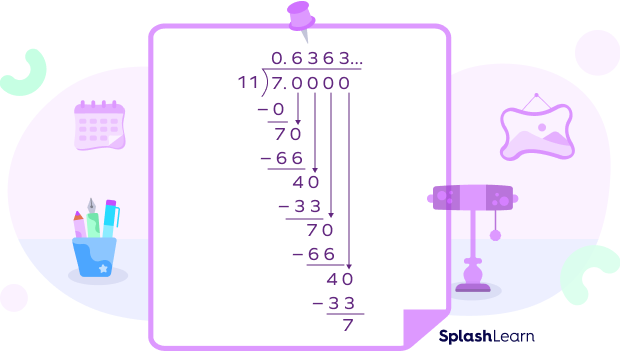
Example 2: $\frac{7}{11} = 0.636363$ …
Decimal Form of a Rational Number Chart
| Rational Number | Decimal form |
|---|---|
| $\frac{1}{2}$ | 0.5 |
| $\frac{99}{2}$ | 49.5 |
| $\frac{1345}{100}$ | 13.45 |
| $\frac{1}{3}$ | 0.333… |
| $\frac{5}{9}$ | 0.5555… |
| $\frac{6}{5}$ | 1.2 |
| $\frac{8}{100}$ | 0.08 |
Facts about Decimal Representation of Rational Numbers
- A rational number has either a terminating decimal expansion or a non-terminating and recurring (repeating) decimal expansion.
- The converse of the above statement is also true. If the decimal expansion of a number is terminating or non-terminating and recurring (repeating), then the number is a rational number.
- The decimal expansion of an irrational number is non-terminating and non-repeating.
Conclusion
In this article, we learned about the two types of decimal expansions of rational numbers. Let’s solve a few examples and practice problems for revision.
Solved Examples on Decimal Representation of Rational Numbers
- Express $\frac{3}{8}$ in the form of a decimal.
Solution:
Divide 3 by 8 using the long division method.
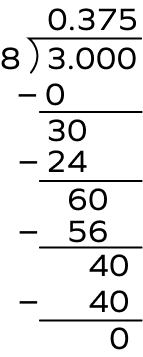
The rational number $\frac{3}{8}$ has a terminating decimal expansion.
$\frac{3}{8} = 0.375$
- What is the decimal expansion of the rational number $\frac{20}{11}$?
Solution:
Divide 20 by 11.
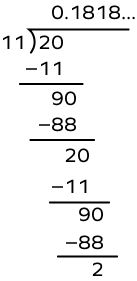
The rational number $\frac{20}{11}$ has a non-terminating and recurring decimal expansion.
$\frac{20}{11} = 0.181818$…
- Write the rational numbers in the decimal form?
i) $\frac{2}{10}$ ii) $\frac{174}{100}$ ii) $\frac{56}{1000}
Solution:
i) $\frac{2}{10} = 0.2$
ii) $\frac{174}{100} = 1.74$
iii) $\frac{56}{1000} = 0.056$
Practice Problems on Decimal Representation of Rational Numbers
Decimal Representation of Rational Numbers: Definition, Types, Facts
What will be the decimal equivalent of the number $\frac{22}{4}$?
Dividing 22 by 4, we get
$\frac{22}{4} = 5.5$
The decimal expansion of a rational number is either terminating or
A rational number has either a terminating or a non-terminating and recurring (repeating) decimal expansion.
Is 1.5 a rational number?
If the decimal expansion of a number is terminating or non-terminating and recurring (repeating), then the number is a rational number. $1.5 = \frac{15}{10} = \frac{3}{2}$
Frequently Asked Questions on Decimal Representation of Rational Numbers
How do you know if a decimal is rational?
If the decimal expansion of a number is “terminating” or “non-terminating and recurring (repeating),” then the number is a rational number.
What cannot be the decimal representation of a rational number?
A rational number cannot have a non-terminating and non-repeating decimal expansion.
What is the difference between rational numbers and fractions?
Rational numbers are the numbers of the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q\neq0$. Fractions represent part of a whole. A fraction is written in the form of $\frac{a}{b}$, where $b\neq0$ and a & b are natural numbers. Here, “a” is the numerator that represents the number of parts taken and “b” is the denominator that represents the total number of parts of the whole.




































