What Is Decimal to Octal Conversion in Math?
The decimal number system consists of 10 digits — 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. It is the most commonly used number system. The octal number system is the base-8 number system and uses the digits 0 to 7.
A number in the octal number system has base 8. A number in the decimal number number system has base 10. Here, we will learn the conversion of a decimal number system to an octal number system. In the decimal to octal conversion, a number in the decimal system is converted into its equivalent octal number.
To convert a decimal number to a binary number, we divide it by 2 (since base is 2), and write remainders in the reverse order. So, how do you convert a decimal number to an octal base? To convert decimal to octal, we divide the number by 8 until we get 0 as the quotient, and then write remainders in the reverse order.
Let’s get to know the steps to convert decimal to octal.
Recommended Games
Steps to Convert Decimal to Octal
The steps to convert a decimal number to its equivalent octal number are as follows:
Step 1: Note down the given decimal number.
Step 2: If the specified decimal number is less than 8, its octal equivalent is the same number.
$0_{10} = 0_{8}$
$1_{10} = 1_{8}$
$2_{10} = 2_{8}$
$3_{10} = 3_{8}$
$4_{10} = 4_{8}$
$5_{10}= 5_{8}$
$6_{10}= 6_{8}$
$7_{10}= 7_{8}$
Step 3: If the number is greater than 7, divide it by 8.
Step 4: Note the remainder we obtain after division.
Step 5: Steps 3 and 4 should be repeated until the quotient is less than 8.
Step 6: Now, write the remainders in reverse order (bottom to top). The outcome is the octal number that corresponds to the given decimal number.
Let’s understand the steps with an example.
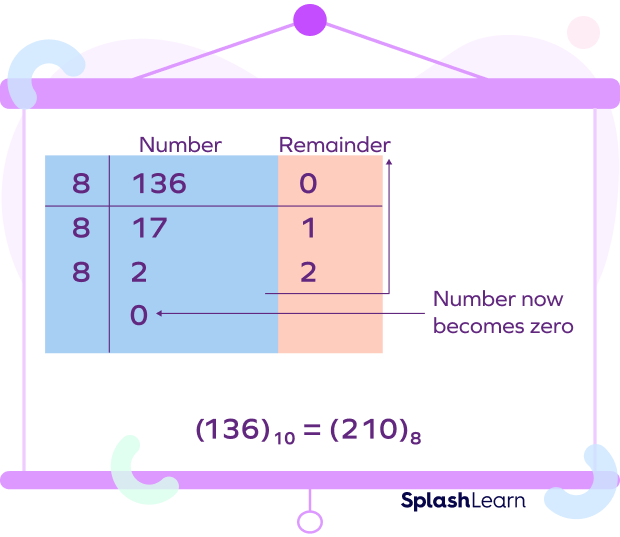
Recommended Worksheets
How to Convert Decimal to Octal
An octal number is a number with base 8, to convert decimal to octal, we start dividing the number by 8 until we get 0 as the quotient and write the acquired remainder in reverse to derive at the equivalent octal number.
Let us learn the methods of conversion of decimals to octals.
Decimal to Octal Conversion Methods
There are two methods of converting decimals to octals:
1. Convert Decimal to Binary to Octal
2. Convert Decimal to Octal
Method 1: Convert Decimal to Binary to Octal
In this method, we first find the binary equivalent of the given number. Once the binary number is obtained, we convert it into an octal number. Let us understand this method using an example.
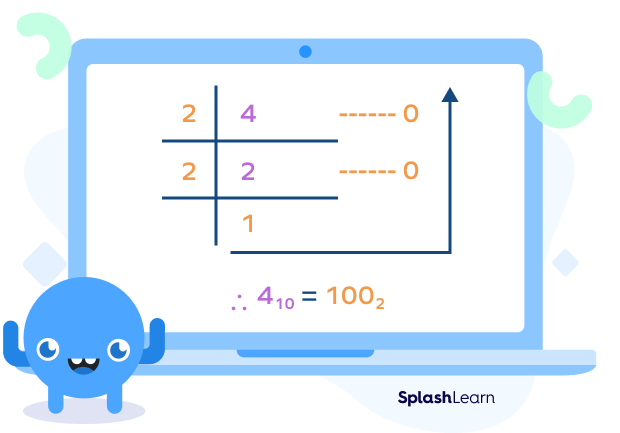
Example: Convert $4_{10}$ to octal.
Step 1: Decimal to Binary
Here, we have to convert $4_{10}$ to binary first. For that, we will divide the given number by 2 as the base of binary numbers is 2.
| Division by 2 | Quotient | Remainder |
|---|---|---|
| $4 \div 2$ | 2 | 0 |
| $2 \div 2$ | 1 | 0 |
| $1 \div 2$ | 0 | 1 |
Writing the numbers downwards to upwards, we get $100_{2}$
Thus, 4 is $100_{2}$ in the binary system.
You can also write this process simply, using the column division as shown below and save your efforts of writing out a big table!
Step 2: Binary to Octal
Now, let us convert $100_{2}$ to the octal system.
Here’s the important part!
Group all the 1s and 0s in the binary number in sets of three, starting from the far right. Add zeros to the left of the last digit if you don’t have enough digits to make a set of three. Identify the octal equivalent of the binary numbers in each group. For that, take a look at the binary to octal conversion table.
Binary to Octal Conversion Table:
| BinaryNumber | OctalNumber |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Alt tag: Binary to octal conversion table
Here, for the binary number 100, we have only one group.
We can see that $100_{2}$ is $4_{8}$ in octal.
Method 2: Convert Decimal to Octal
In this method, the decimal number is divided by 8, each time a reminder is obtained from the previous digit. Once the quotient is less than 8, we obtain the octal number by writing the remainder in reverse order. If the given decimal number is less than 8 the octal number is the same.
Let us understand this with the help of an example.
Example: Convert $416_{10}$ to octal.
Divide the given number by 8.
| Division by 8 | Quotient | Remainder |
|---|---|---|
| $416 \div 8$ | 52 | 0 |
| $52 \div 8$ | 6 | 4 |
| $6 \div 8$ | 0 | 6 |
Since the quotient is zero now, we stop the division.
So, by taking the remainders in reverse order, we get the equivalent octal number.
Hence, $(416)_{10} = (640)_{8}$
Note that we can also represent this division as shown below:
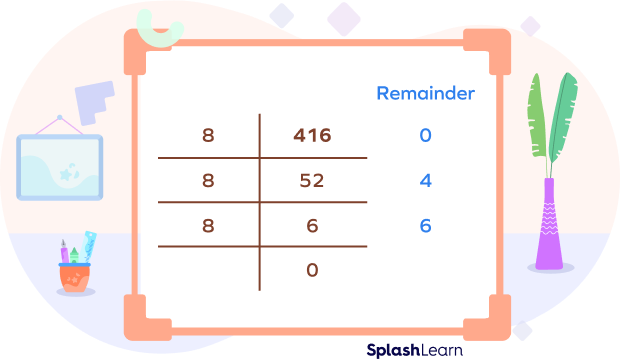
Write remainders in reverse order to get the octal number.
$416_{10} = 640_{8}$
Decimal to Octal Conversion Table
| Decimal | Equivalent Octal Number | Decimal | Equivalent Octal Number |
|---|---|---|---|
| 0 | 0 | 9 | 11 |
| 1 | 1 | 10 | 12 |
| 2 | 2 | 11 | 13 |
| 3 | 3 | 12 | 14 |
| 4 | 4 | 13 | 15 |
| 5 | 5 | 14 | 16 |
| 6 | 6 | 15 | 17 |
| 7 | 7 | 16 | 20 |
| 8 | 10 | 17 | 21 |
Alt tag: Decimal to octal conversion table
Decimal to Octal Conversion with Decimal Point
Decimals have a whole number part and a fractional part separated by a decimal point. To convert a decimal number into octal, we first convert the whole number part into octal form and then convert the fractional part into octal form. And finally we combine the two results to get the final answer.
Example: Convert 7.16 into octal form.
Step 1: Separate the decimal number
Separate the decimal number into two parts: the whole number and the fractional part.
So, $7.16 = 7 + 0.16$.
Step 2: Convert the whole number part into octal.
Here, $(7)_{10} = (7)_{8}$
Step 3: Convert the fractional part 0.16 into octal. Multiply the fractional part by 8. Again divide the product into two parts. Multiply the fractional part by 8 until the fractional part is equal to zero.
| Multiply by 8 | Result | Whole part | Fractional part |
|---|---|---|---|
| $0.16 \times 8$ | 1.28 | 1 | 0.28 |
| $0.28 \times 8$ | 2.24 | 2 | 0.24 |
| $0.24 \times 8$ | 1.92 | 1 | 0.92 |
| $0.92 \times 8$ | 7.36 | 7 | 0.36 |
| $0.36 \times 8$ | 2.88 | 2 | 0.88 |
Take the necessary digits after the decimal point. Now, we have 5 digits as an answer.
Write all the whole number parts from top to bottom that derives the octal number of the fractional number.
Hence, $0.16 = 0.12172$…
$0.16_{Base\; 10} = 0.12172…_{Base\; 8}$
$0.16_{10} = 0.12172…_{8}$
Step 4: Add the two octal results.
$(7)_{10} = (7)_{8}$
$(0.16)_{10} = (0.12172..)._{8}$
So, $(7.16)_{10} = (7.12172..)_{8}$
or $(7.16)_{10} = (7.12172)_{8}$ (approx. value)
Facts about Decimal to Octal Conversion
- The “dec” in decimal means ten and refers to the fact that each position in a decimal number corresponds to ten times more than the next position. For example, the number 325 means 3 hundreds, 2 tens, and 5 ones.
- Humans decided to group in tens because that’s how many fingers we have. It made counting and arithmetic a whole lot easier!
- In 1801, James Anderson criticized the French for basing the metric system on decimal arithmetic. He suggested base 8, for which he coined the term octal.
- The main advantage of using the octal number system is that it uses fewer digits than the decimal and hexadecimal number system. So, it has fewer computations and less computational errors.
- The octal number system is widely used in computer application sectors and digital numbering systems. The octal number is also used in the aviation sector in the form of a code.
Conclusion
In this article, we have learnt decimal to octal conversion with steps and methods. Let us solve some decimal to octal examples to grasp the concept better.
Solved Examples on Decimal to Octal Conversion
Example 1: Convert $52_{10}$ to octal.
Solution:
| Division by 8 | Quotient | Remainder |
|---|---|---|
| $52 \div 8$ | 6 | 4 |
| $6 \div 8$ | 0 | 6 |
Writing remainders in reverse order, we get the equivalent octal number.
Hence, $(52)_{10} = (64)_{8}$
Example 2: Convert $18_{10}$ to octal. (Use the method “decimal to binary to octal.”)
Solution:
Decimal to Binary:
First, let us convert the given decimal number 18 into a binary number.
To convert decimal to binary, we have to divide the given decimal number by 2.
| Division by 2 | Quotient | Remainder |
|---|---|---|
| $18 \div 2$ | 9 | 0 |
| $9 \div 2$ | 4 | 1 |
| $4 \div 2$ | 2 | 0 |
| $2 \div 2$ | 1 | 0 |
| $1 \div 2$ | 0 | 1 |
Therefore, the binary equivalent for the given decimal number $18_{10}$ is $10010_{2}$.
Binary to Octal:
Now, lets convert $10010_{2}$ to octal.
Group all the 1s and 0s in the binary number in sets of three, starting from the far right. Add zeros to the left of the last digit if you don’t have enough digits to make a set of three.
$10010_{2} = 010 | 010_{2}$ …two groups of 3 digits
Identify the octal equivalent of the binary numbers in each group using the conversion table.
Here, $010_{2} = 2_{8}$
Thus, $010010_{2} = 22_{8}$
So, the octal value of $10010_{2}$ is $22_{8}$.
Example 3: Convert 350.2 into octal form.
Solution:
Separate the decimal number into two parts: the whole and the fractional. So, $350.2 = 350 + 0.2$.
First, we will convert 350 into octal form. We will divide 350 by 8 until you get a quotient of zero.
| Division by 8 | Quotient | Remainder |
|---|---|---|
| $350 \div 8$ | 43 | 6 |
| $43 \div 8$ | 5 | 3 |
| $5 \div 8$ | 0 | 5 |
Hence, 350 is 536 in octal number.
Now, we will convert the fractional part 0.2 into octal. Let’s take only 5 digits.
| Multiplied by 8 | Result | Whole | Fractional Part |
|---|---|---|---|
| $0.6 \times 8$ | 1.6 | 1 | 0.6 |
| $0.6 \times 8$ | 4.8 | 4 | 0.8 |
| $0.8 \times 8$ | 6.4 | 6 | 0.4 |
| $0.4 \times 8$ | 3.2 | 3 | 0.2 |
| $0.2 \times 8$ | 1.6 | 1 | 0.6 |
We will write all the integer parts from top to bottom that derives the octal number of the fractional number.
Hence, $0.2 = 0.14631$
Now, adding the integer and fractional part will give us an octal number.
$536 + 0.14631463 = 536.14631$
Thus, the octal number of 350.2 is 536.14631.
Practice Problems on Decimal to Octal Conversion
Decimal to Octal: Steps, Methods, Conversion Table
How many digits does the decimal number system use?
The decimal number system uses digits from 0 to 9 to form other numbers.
How many digits does the octal number system use to represent all the numbers?
The Octal number system uses digits from 0 to 7 to form other numbers.
The equivalent octal number of decimal number 5 is _________.
The equivalent octal numbers of decimal numbers from 0 to 7 are the same.
Based on the following division table, we can say that $100_{10} =$
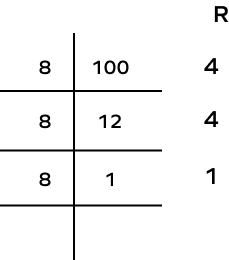
We write the remainders obtained in the division in the reverse order.
Thus, $100_{10} = 144_{8}$
Frequently Asked Questions on Decimal to Octal Conversion
What is an octal number system?
The octal number system is the number system with base 8. It uses the eight digits 0, 1, 2, 3, 4, 5, 6, and 7.
How do you convert octal to decimal?
The octal to decimal conversion is done by using its base number and place values. Here, we convert octal to decimal or base 8 to decimal (base 10). Find the position of every digit. We should count the position from the right direction of the number. The position count starts from 0. Multiply every digit with 8 to the power of their corresponding position. Finally, calculate the sum of all the multiples.
For example, let’s convert $(16)_{8}$ to decimal.
$(16)_{8} = (1 \times 8^{1}) + (6 \times 8^{0}) = 8 + 6 = (14)_{10}$
What is the hexadecimal number system ?
The “hexadecimal” numbering system uses the base of 16 system. Their format is quite compact and much easier to understand compared to the long binary strings of 1s and 0s. The hexadecimal numbering system uses 16 (sixteen) different digits with a combination of numbers from 0 through to 15.
How can we convert binary to octal?
Octal numbers are the numbers that can be derived from 3 bits of binary numbers. Group all the 1s and 0s in the binary number in sets of three, starting from the far right. Add zeros to the left of the last digit if you don’t have enough digits to make a set of three. Identify the octal equivalent of the binary numbers in each group. For that, take a look at the binary to octal conversion table.
Example: $011010110_{2} = 011| 010 | 110_{2} = 326_{8}$




































