Consider a situation where you buy 24 cans of water bottles at $\$$3.99. How would you find the price of one can? By dividing $\$$3.99 by 24! Dividing decimals is very much like dividing whole numbers. You just have to understand where the decimal point must be placed. Let’s explore the process of dividing decimals in more detail. But before that, let’s understand what decimals are.
What Is a Decimal Number?
A decimal number is a number that has a whole number part and the fractional part separated by a dot. The dot in a decimal number is called a decimal point. The digits following the decimal point show a value smaller than one.
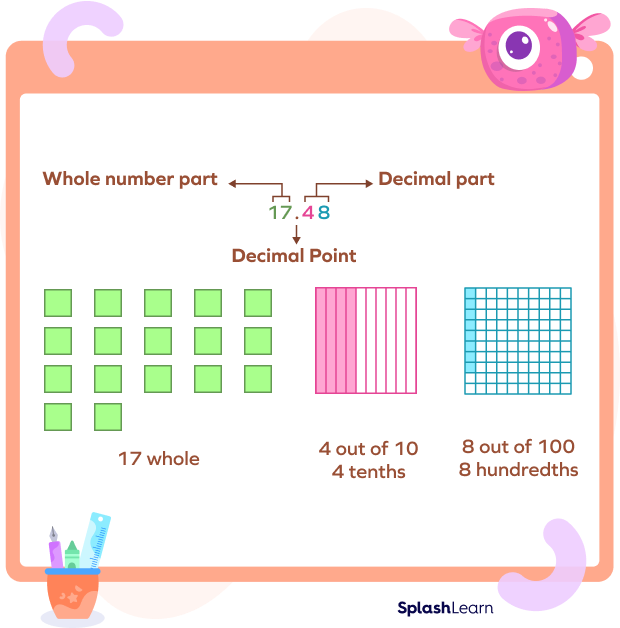
In the decimal number 17.48, 17 is the whole number part and 48 is known as the decimal part or fractional part.
Recommended Games
How to Divide Decimals?
Dividing Decimal numbers is similar to dividing whole numbers. We just have to take care of the correct position of the decimal point. Let’s discuss three different examples related to division of decimals.
Dividing Decimals Examples
Take a look at the following examples.
Example 1: Dividing $\$$25.5 dollars among 5 friends.
Examples 2: Dividing the decimal 1.21 by the decimal number 1.1
Example 3: Dividing the decimal number 23.56 by 1000.
So, we can see that there can be three types:
- Dividing decimals by whole numbers.
- Division of a decimal number by another decimal number.
- Division of decimals by 10, 100, and 1000.
Dividing Decimals by Whole Numbers
Let’s understand dividing decimals by whole numbers through an example.
Consider 120.6 24.
The following are the steps to divide 120.6 by 24:
The dividend is the number that is getting divided and the divisor is the number that divides the dividend. Here, 120.6 is the dividend and 24 is the divisor.

So, $120.6 24 = 5.025$
Dividing a Decimal Number by Another Decimal Number
Let’s understand dividing decimals by another decimal number using an example. Let’s divide 4.88 by 0.4. Here, 4.88 is the dividend and 0.4 is the divisor.
The following are the steps he will use for the division:
- Step 1: Since we already know how to divide a decimal number by a whole number, convert the divisor into a whole number. In this example, we convert 0.4 into 4 by moving the decimal point one position to the right. In this example, 0.4 will become 4.

- Step 2: Move the decimal point in the dividend the same number of places as in the divisor. Moving the decimal point one position to the right in 4.88 gives 48.8.

- Step 3: Now divide the decimal number 48.8 by the whole number 4. This is equivalent to dividing the decimal 4.88 by 0.4.

Dividing Decimals by 10, 100, and 1000
The division of a decimal number by 10, 100, and 1000 is quite simple. Let’s discuss each type.
Division by 10
Consider $82.5 \div 10$.
Dividing a decimal by 10 simply changes the position of the decimal point one place to the left.

$8251010=82510110=825100=8.25$
Division by 100
Consider $98.6 \div 100$.
Dividing the decimal number by 100 shifts the decimal point two positions to the left.

Also, $98610100=986101100=9861000=0.986$
Division by 1000
Consider $8.725 \div 1000$.
Now since the decimal number is divided by 1000, the decimal point will shift three places towards the left in the quotient.

Also, $872510001000=8725100011000=87251000000=0.008725$
Recommended Worksheets
Fun Facts
While dividing a decimal number by a whole number or by another decimal number, there are cases when we end up with a remainder of 0. Such decimal numbers are called Terminating Decimals.
For example: $62.35 \div 5 = 12.47$
However, there can also be a case when the remainder never becomes 0 and the long division process goes on. Such decimal numbers are called Non-terminating Decimals.
Non-terminating decimals can be of two types:
a. Recurring/Repeating decimals like 0.2666666666 . . .
b. Non-recurring/Non-repeating decimals like 1.7320508 . . .
Solved Examples
1. Divide 67.25 by 10.
Solution: On dividing 67.25 by 10, we shift the decimal point one position to the left.
We get
$67.25 \div 10 = 6.725$.
2. If the total weight of 3 oatmeal cookies is 31.5 grams, then what will be the total weight of 5 oatmeal cookies?
Solution: Total weight of 3 oatmeal cookies $= 31.5$ g
Weight of 1 oatmeal cookie $= 31.5 \div 3 = 10.5$ g
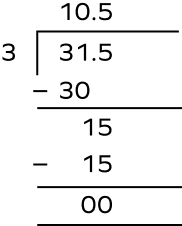
Total weight of 5 oatmeal cookies $= 10.5 \times 5 = 52.5$ g
3. A wooden plank of length 3.5 feet is divided into small pieces of length 0.07 foot. How many small pieces will be formed?
Solution: Length of wooden plank $= 3.5$ feet
Length of each small piece $= 0.07$ feet
Since we are dividing the plank into small pieces of equal length, we divide 3.5 by 0.07.
Shift the decimal point two positions to the right in both 0.07 and 3.5 to perform the division.
Number of small pieces $= 3.5 \div 0.07$
$= 350 \div 7$
$= 50$
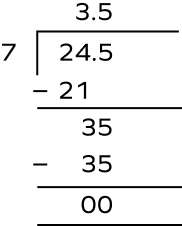
4. George has $24.5 of his monthly allowance left with him. He spends it over the course of a week such that his daily expenses stay the same. How much money does he spend every day?
Solution: Money George has with him $= $\$$24.5$
This amount is equally spent in a week or 7 days.
Amount spent by George every day $= 24.5 \div 7 = $\$$3.5$
5. Amanda made two trips to visit her parents. She drove 432.78 miles in total. How far did Amanda drive on each trip?
Solution: Total distance Amanda drove $= 432.78$ miles
Number of trips she took $= 2$
Distance traveled on each trip $= 432.78 \div 2 = 216.39$ miles

Practice Problems
Dividing Decimals - Meaning With Examples
On dividing 439.4 by 100, we get
Dividing by 100 will shift the decimal point two positions to the left.
So, $439.4 \div 100 = 4.394$
$34.56 \div 1000 =$
Dividing by 1000 will shift the decimal point three positions to the left.
So, $34.56 \div 1000 = 0.03456$.
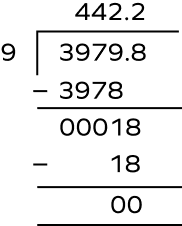
On dividing 397.98 by 0.9, we get:
Shift decimal point in 0.9 and 397.98 one position to the right before performing the division.
So, $3979.8 \div 9 = 442.2$
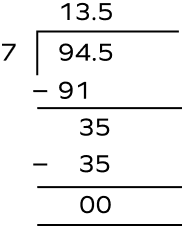
Mark bought 7 pencils for $\$$94.5. What would be the price of one pencil?
Total cost of 7 pencils $=$ $\$$94.5
Cost of one pencil $= 94.5 \div 7 =$ $\$$13.5
A shopkeeper produced 724.98 gallons of fresh apple juice over the course of 3 days. How much apple juice was produced each day if he produced equal quantities each day? (Round your answer to the nearest tenth.)
Capacity of fresh apple juice made by shopkeeper $= 724.98$ gallons
Number of days $= 3$
Capacity of fresh apple juice made on 1 day $= 724.98 \div 3 = 241.66$ gallons $241.7$ gallons
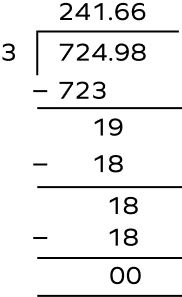
Frequently Asked Questions
Can remainder be a decimal number while performing division?
No, the remainder can never be a decimal number while performing division.
How many places will the decimal point shift if a decimal number is divided by 10,000?
There are 4 zeroes in 10,000. So, the decimal point will shift 4 places to the left.
How to divide a whole number by a decimal?
We first convert the divisor into a whole number by shifting the decimal point. We make a similar shift in the dividend and then perform the division.
For example: Divide 12 by 0.4.
Change the divisor 0.4 to 4 by shifting the decimal point one place to the right.
Similarly, after shifting the decimal point 12, we get 120.
Thus, $12 \div 0.4 = 120 \div 4 = 30$.
Can the quotient be a decimal number when two whole numbers are divided?
Yes, the quotient can be a decimal number when one whole number does not divide the other whole number completely. For example, $4 \div 5 = 0.8$




































