The expanded form with decimal numbers is the mathematical expression to show the sum of the values of each digit in the number. Let’s learn more about decimals, place value, and expanded forms below.
What is Decimals?
A decimal number is a number that consists of a whole number and a fractional part. The decimal point separates the whole number from the fractional part.
In a decimal number, the digits to the left of the decimal point represent a whole number. The digits to the right of the decimal represent the parts.
As we move towards right after the decimal point, the place value of the digits becomes 10 times smaller.
The first digit on the right of the decimal point means tenths i.e. $\frac{1}{10}$. The next place becomes ten times smaller and is called the hundredths i.e. $\frac{1}{100}$ and so on.
For example,
In 31.356, 31 is the whole number part, 3 is in tens place and its place value is 30,
1 is in ones place, and its place value is 1.
There are three digits to the right of the decimal point,
3 is in the tenths place, and its place value is 0.3 or $\frac{3}{10}$
5 is in the hundredths place, and its place value is 0.05 or $\frac{5}{100}$
6 is in the thousandths place, and its place value is 0.006 or $\frac{6}{1000}$
Recommended Games
Expanded Form
In the expanded form. We break up a number according to its place value and expand it to show the value of each digit.
For example, the expanded form of 254 is given.
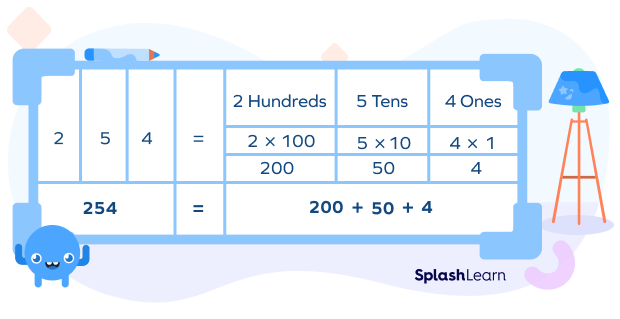
Thus, the expanded form of the number $254$ is $200 + 50 + 4$.
Recommended Worksheets
Expanded Form of Decimal Numbers
The expanded form with decimals is the mathematical expression to show the sum of the values of each digit in the number. Writing decimals in an expanded form simply means writing each number according to its place value. Before the decimal point, the expanded form is the same as it is for whole numbers. After the decimal point, it is different.
When you write a decimal number in its expanded form, you are expressing the number separated into its composite individual place values and decimal values if necessary in the form of an expression.
Likewise, the expanded form of a number with a decimal or a fraction is written with a base 10-multiple denominator, represented by the power of 10.
For example, the number 3.482 in its expanded form is written as:
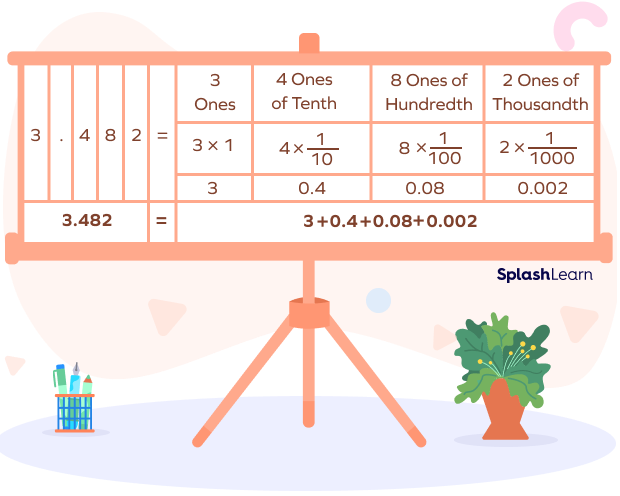
The expanded form of the number 3.482 is:
$= 3 +$ 4⁄10 + 8⁄100 + 42⁄1000 ,or
$= 3 + 0.4 + 0.08 + 0.002$
How to Write a Decimal in an Expanded Form?
Writing decimals in expanded form can be achieved by following the steps given below.
Suppose we want to expand 1.234.
Step 1: We start from the left hand side first. We have ones place, i.e., 1.
Step 2: Next, we have the first decimal place, the tenths. We take 2 and multiply it by fraction $\frac{1}{10}$.
$1+(2\times\frac{1}{10})$
Step 3: Then, we have the hundreds place. We move to a higher multiple of 10 for the denominator. In other words, we multiply 3 by fraction 1100.
$1+(2\times\frac{1}{10})+(3\times\frac{1}{100})$
Step 4: Finally, we have the thousands place. Add another 0 in the denominator. We multiply 4 by $\frac{1}{1000}$.
$1+(2\times \frac{1}{10})+(3\times \frac{1}{100})+(4\times\frac{1}{1000})$
Hence, the expanded form of $1.234$ is $1+0.2+0.03+0.004$.
Standard Form
Writing a number in standard form (or numeric form) is the opposite or reverse of writing a number in expanded form.
For example, the standard form for $1+0.2+0.03+0.004$ is $1.234$.
Expanded form and standard form are opposites of each other.
Application of Expanded Form with Decimals
The scope of decimal numbers is in the areas where accuracy and precision are required. The concept of the expanded form is useful in comprehending the value of a number as well as the numeric value of a quantity.
Fun Facts
- The weights in the ratios of 1⁄20 , 1⁄10 , 1⁄5 , 1⁄2 and multiples of 10 were used in the Indus Valley civilization for the purpose of trade.
- Rod calculus in ancient China used bamboo strips with the decimal system for math operations like multiplication during 305 BCE.
- Mathematician Archimedes invented a decimal positional system for Sand Reckoner to represent large numbers that were multiples of 10.
Solved Examples
Example 1. Write 8.12 in its expanded form.
Solution: The expanded form of $8.12=8+0.1+0.02$
Example 2. Write $7 + 0.8 + 0.09 + 0.003$ in standard form.
Solution: The standard form is 7.893.
Example 3. What will be the place value of 4 in 56.924?
Solution: The place value of 4 in 56.924 will be $4 \times \frac{1}{1000} = 0.004$.
Practice Problems
Expanded Form With Decimals - Definition with Examples
The standard form of $50 + 8 + 0.7 + 0.06 + 0.005$ is
The standard form of $5 \times 10 + 8 \times 1 + 7 \times 0.1 + 6 \times 0.01 + 5 \times 0.001$
$= 50 + 8 + 0.7 + 0.06 + 0.005$
$= 58.765$.
The expanded form of 123.45 is
The expanded form of 123.45 is
$= 1 \times 100 + 2 \times 10 + 3 \times 1 + 4 \times 0.1 + 5 \times 0.01$
$= 100 + 20 + 3 + 0.4 + 0.05$.
The place value of 6 in 987.65 is
The expanded form of 987.65 is
$= 900 + 80 + 7 + 0.6 + 0.05$.
The place value of 6 in 987.65 is 0.6.
Conclusion
The expanded form is nothing but a technique of rewriting a number by including the values of the digits. Given above was everything you needed to know about the expanded form.
Frequently Asked Questions
What is the difference between expanded form and standard form?
In the expanded form, the digits of the number are split into each of the individual digits with their place value and written in expanded form. The standard form is the combination of digits written together as a single number.
How is expanded form with decimals used?
The concept of expanded form with decimals is useful in comprehending the value of a number as well as the numeric value of a quantity.
Is expanded form the same as expanded notation?
No. Let’s understand the difference between the expanded form and expanded notation using an example.
Expanded notation with decimals: $527 = (5\times100) + (2\times10) + (7\times1)$
Expanded form with decimals: $527 = 500 + 20 + 7$
The expanded notation is a more detailed form. Every digit is multiplied by its corresponding place value (ones, tens, hundreds, etc.). However, in the expanded form, this step is skipped and the final product is written.




































