Diagonal of a Cube Formula – Definition, Derivation, Examples

What Is the Diagonal of a Cube Formula?

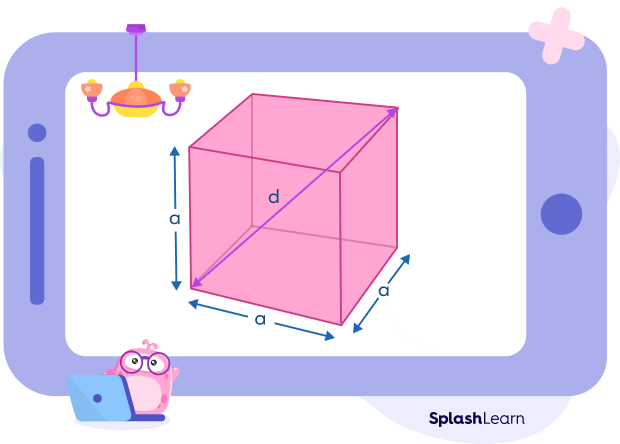
The formula to calculate the length of diagonal of a cube (body diagonal) is 3 times the length of one of its sides. In mathematical terms, if “s” represents the length of a side, then the diagonal “d” can be expressed as $d = s\sqrt{3}$. 

A cube is a three-dimensional solid figure with 6 congruent square faces, 8 vertices, and 12 equal edges. All its edges are equal in length. This indicates that a cube has equal length, breadth, and height and that every one of its sides is a square.

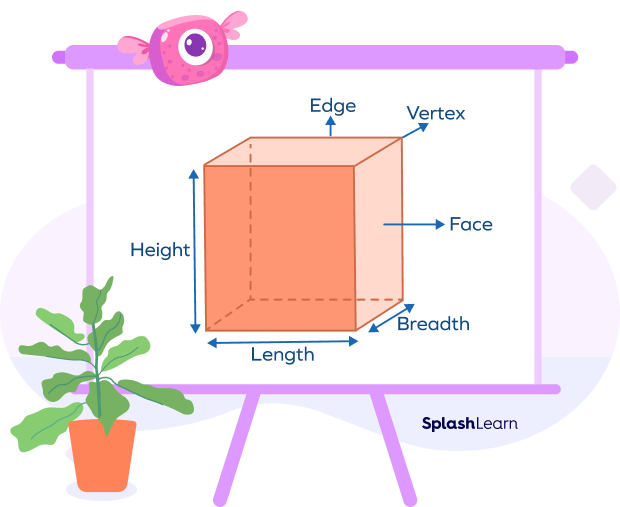
The diagonal of a cube is the line segment that connects any pair of non-adjacent sides of the cube. The main diagonal of a cube is the one that goes through the center of the cube; the face diagonal of a cube is not its primary diagonal. 

There are two kinds of diagonals of a cube.

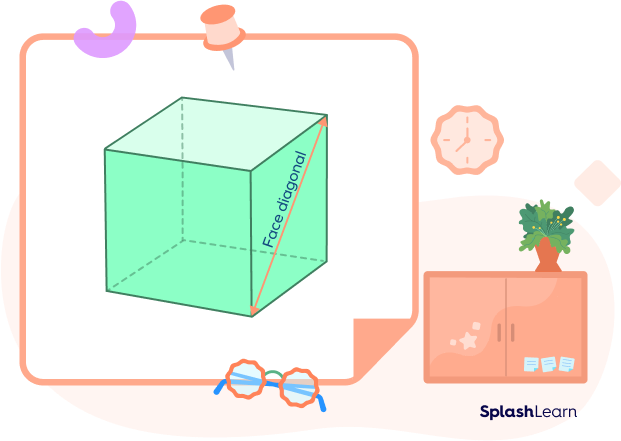
• Face Diagonal of a Cube

There are six square-shaped faces on a cube. The non-adjacent vertices of each face are connected by two diagonals. Therefore, there are actually 12 face diagonals.

• Body Diagonal of a Cube

The body diagonals connect the two opposite vertices of the cube by passing through the internal structure of the cube. As a result, there are 4 diagonals crossing across the body. It is also known as “space diagonal,” or “internal diagonal,” or “main diagonal.”

Diagonal of a Cube Formula

Let’s see the formulas to find the diagonal of a cube.

Type of Diagonal	Diagram	Formula
Face Diagonal		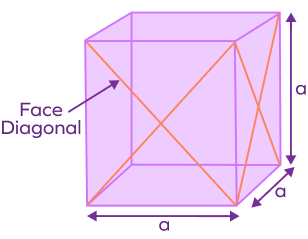$d = \sqrt{2a}$ where “a” is the length of the side of a cube.
Body Diagonal		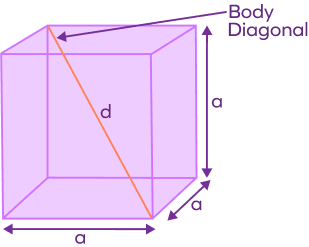$d = \sqrt{3a}$ where “a” is the length of the side of a cube.

Example 1: Calculate the length of the face diagonal of a cube whose each side is 8 inches long.

Length of the side of the cube = a = 8 inches

Length of face diagonal of the cube $= \sqrt{2a}$

$\Rightarrow d = \sqrt{2} \times 8$

$\Rightarrow d = 1.41 \times 8$

$\Rightarrow d = 11.28$ inches

Example 2: Calculate the length of the body diagonal of a cube with side-length of 9 inches.

Length of the side of the cube = a = 9 inches

Length of body diagonal of the cube $= \sqrt{3a}$

$d = \sqrt{3} \times 9$

$d = 1.73 \times 9$

Length of body diagonal of the cube $= 15.57$ inches

Number of Diagonals in a Cube

We know that a cube has 6 faces. Each face has 2 diagonals connecting their non-adjacent sides. 

Number of face diagonals $= (2 \times 6) = 12$ 

Additionally, there are 4 diagonals running across the body of the cube. 

Number of body diagonals $= 4$

Therefore, the total no. of diagonals in a cube can be calculated as 

$12 + 4 = 16$

Derivation of Diagonal of a Cube Formula

The formula for the diagonal of a cube is calculated using the Pythagoras theorem. The cube diagonal formula is usually referred to as the body diagonal formula. 

Consider a cube whose each side length is “a” units. If we draw any face diagonal, we can form a right-angled triangle with legs of “a” units and face diagonal as the hypotenuse.

Face diagonal $= \sqrt{a^{2} + a^{2}} = \sqrt{2a^{2}} = \sqrt{2a}$ units 

Similarly, we will get a right-angled triangle with the body diagonal as the hypotenuse, side of the cube as one leg, and the face diagonal as the other leg.

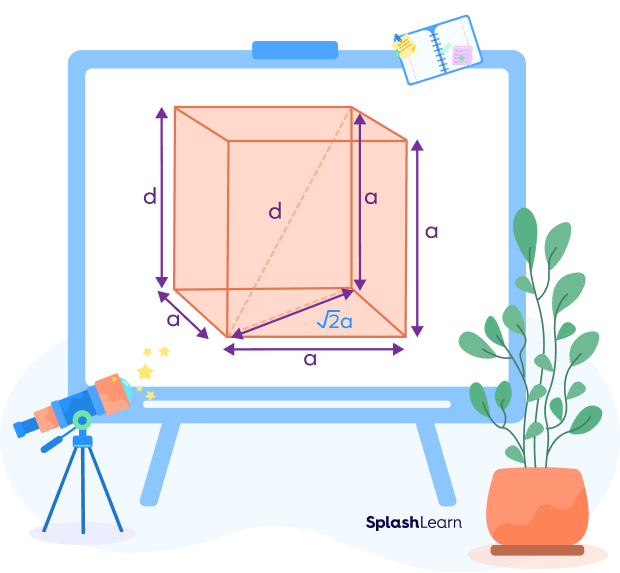
Side length = a 

face diagonal $= \sqrt{2a}$

By Pythagoras theorem, we get

$a^{2} + (\sqrt{2a})^{2} = d^{2}$

$\Rightarrow a^{2} + 2a^{2} = d^{2}$

$\Rightarrow 3a^{2} = d^{2}$

$\Rightarrow d = \sqrt{3a^{2}}$

$\Rightarrow d = \sqrt{3a}$

Length of the Body diagonal $= d = \sqrt{3a}$

Uses of Diagonal of a Cube Formula

1. Determining Cube Size: The formula helps figure out how long the diagonal is within a cube, which is like measuring the longest diagonal in a rectangular box.
2. Visualizing 3D Shapes: Understanding cube diagonals gives you a way to imagine how lines can go from one corner of the cube to the farthest corner, helping you see how 3D shapes fit together.
3. Understanding Big Structures: Architects and builders use these diagonals to make sure big structures, like bridges or buildings, are strong and stable when they have cube-like parts.
4. Creating Cube Designs: If you want to build something using cubes, like a robot or a piece of furniture, knowing how diagonals work will help you make sure everything fits together just right.

Facts about the Diagonal of a Cube Formula

Conclusion

In this article, we explored the formulas for calculating the face and body diagonals of a cube, crucial for determining distances between vertices. These concepts are pivotal in geometry and spatial reasoning. For enhanced understanding, let’s work through examples and engage in MCQs.

Solved Examples on Diagonal of a Cube Formula

Example 1: Find the face diagonal of a cube with sides of 7 units. 

Solution: 

Length of the side of the cube = 7 units

Length of face diagonal of the cube $= \sqrt{2a}$

Length of face diagonal of the cube $= \sqrt{2} \times 7$

Length of face diagonal of the cube $= 1.41 \times 7$

Length of face diagonal of the cube $= 9.87$ units

Example 2: What will be the body diagonal of a cube with sides of 11 inches?

Solution: 

Length of the side of the cube = 11 inches

Length of body diagonal of the cube $= \sqrt{3a}$

Length of body diagonal of the cube $= \sqrt{3} \times 11$

Length of body diagonal of the cube $= 1.73 \times 11$

Length of body diagonal of the cube =19.03 inches

Example 3: The body diagonal of a cube is 4√3 units. What will be the length side of the cube and the length of the face diagonal of the cube?

Solution: 

Length of body diagonal of the cube $= \sqrt{3a}$

$\sqrt{3a} = 4\sqrt{3}$

Length of side of the cube =4 units

Length of the side of the cube =4 units

Length of face diagonal of the cube $= \sqrt{2a}$

Length of face diagonal of the cube $= \sqrt{2} \times 4$

Length of face diagonal of the cube $= 1.41 \times 4$

Length of face diagonal of the cube $= 5.64$ units

Practice Problems on Diagonal of a Cube Formula

Frequently Asked Questions about the Diagonal of a Cube Formula