Direct Proportion: Definition, Formula, Symbol, Examples, FAQs

What Is Direct Proportion in Math?

Direct proportion or direct variation is a type of proportion in which the ratio of two quantities stays constant. 

Suppose a variable y varies directly with x, then it means that if x increases, y increases by the same factor. If x decreases, then there is a proportionate decrease in y also.

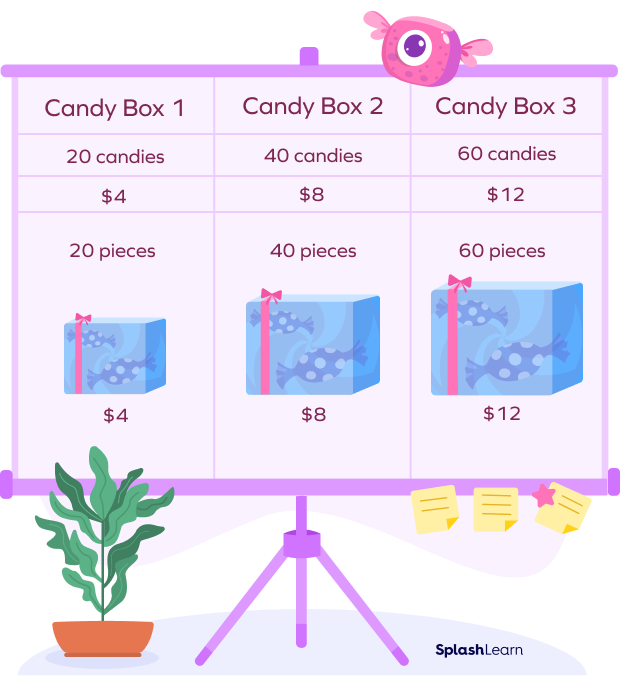
Direct Proportion Example: 

The cost of the candy increases as the number of the same increases.

Direct Proportion Symbol

The “directly proportional symbol” or “direct proportional symbol” is $\propto$. 

We read x ∝ y as “x is directly proportional to y.” 

It means that x is dependent on y.

We read y ∝ x as “y is directly proportional to x.” 

It means that y is dependent on x.

Direct Proportion Formula

If y is directly proportional to x, then the direct proportion formula or the direct proportion equation is given by y=kx, where k is a constant of proportionality.

Constant of Proportionality

From the direct proportion formula, we have y = kx.

The fixed value $k = \frac{y}{x}$ is called the constant of proportionality and it represents the constant ratio between the two quantities that are in direct proportion. k can be any non-zero real number.

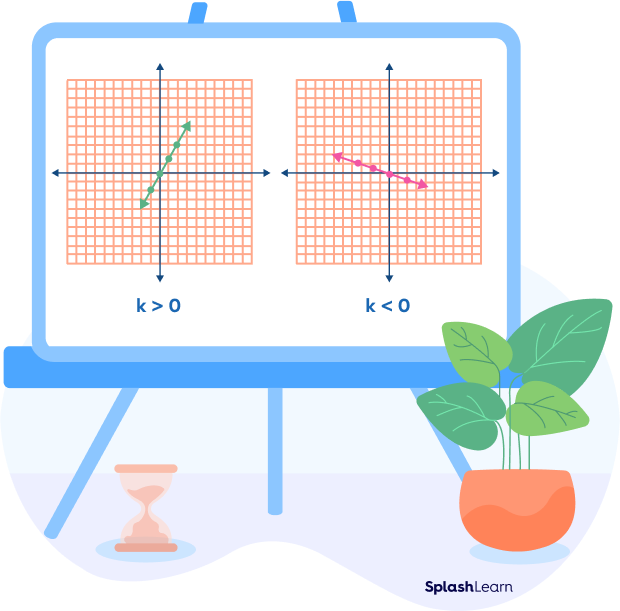
Direct Proportion Graph

If you construct a graph of a direct proportion, it always comes out to be a straight line passing through the origin (0, 0).

The slope of this line is k.

• If k is negative, the line goes down from left to right.
• If k is positive, the line rises from left to right.

Difference between Direct Proportion and Inverse Proportion

Direct proportion and inverse proportion are two kinds of proportional relationships in math describing the relation between two variables. Here are their key differences in the table below:

Criteria	Direct Proportion	Inverse Proportion
Definition	A relationship where two variables increase or decrease together, maintaining a constant ratio	A relationship between two variables when one increases and the other decreases and vice versa, such that the product of their corresponding values remains constant
Symbol	$y \propto x$	$y \propto \frac{1}{x}$
Formula	$y = kx$ y is the dependent variable. x is the independent variable. k is the constant of proportionality. x and y vary directly.	$y = \frac{k}{x}$ x and y are two variables. k is the constant of proportionality. x and y vary inversely.
Graph	It is a straight line.	It is a hyperbolic curve.
Examples	As speed increases, the distance covered increases and vice versa.	The number of workers for work and the amount of time for work completion.More the workers, the less time is taken for completion of the work and vice versa.

How to Use Direct Proportion to Solve Problems

Let’s understand this with the help of an example.

Example: If 20 pens cost $25, what would be the cost of 100 pens?

Here, the cost of pens is directly proportional to the number of pens.

Note down the given values of x and y. 

Number of pens	Cost of pens
20	$\$25$
100	?

Since the quantities are in direct proportion, their ratio is constant.

$\frac{20}{25} = \frac{100}{?}$

By cross multiplying, we get

$20 \times ?= 100 \times 25$

? $= \$125$

100 pens will cost $\$125$.

Facts about Direct Proportion

Conclusion

In this article, we learned about direct proportion, its graph, formula, equation, and examples. Let’s solve a few examples and practice problems to understand the concept better.

Solved Examples of Direct Proportion

1. If 8 rooms are required for 24 guests, how many rooms would be required to accommodate 12 guests?

Solution:

Number of rooms	Number of guests
24	8
y = ?	12

Here, $\frac{24}{8} = \frac{w}{12}$

Cross-multiply:

$w \times 8 = 12 \times 24$

w = 36

Therefore, for 12 guests, a total of 36 rooms will be required. 

2. If 4 tasks take 8 hours for completion, how many tasks can be completed in 20 hours?

Solution:

Number of tasks	Number of hours
4	8
n = ?	20

Let’s write the constant ratios.

$\frac{4}{8} = \frac{n}{20}$

$n = 10$

In 20 hours, 10 tasks can be completed.

3. What will 10 movie tickets cost if the price of 6 tickets is $\$36$?

Solution:

6 tickets cost $\$36$.

Let 10 movie tickets cost $y.

$\frac{6}{36} = \frac{10}{6}$

$y \times 6 = 36 \times 10$

$y = \$60$

4. If a task is completed in 20 days by 5 workers, how long will it take 10 workers to perform the same task?

Solution: 

This problem can again be solved using the direct proportion formula.

Let the number of days for 10 workers to complete the task be x.

$\frac{5}{10} = \frac{20}{x}$

Cross-multiply

$5x = 10 \times 20$

Simplify.

$x = \frac{(10 \times 20)}{5}$

$x = 40$

Therefore, 10 workers will require 40 days to complete the same task.

5. How far can John run in 60 minutes if he can cover 9 miles in 90?

Solution: 

Use the direct proportion formula for this problem.

Let the distance John covers in 60 minutes be x.

$\frac{9}{90} = \frac{x}{60}$

Cross-multiply.

$\frac{9 \times 60} = 90x$

Simplify.

$x = \frac{(9 \times 60)}{90}$

$x = 6$

Therefore, John can run 6 miles in an hour.

Practice Problems on Direct Proportion

Frequently Asked Questions about Direct Proportion