Distance Between Point and Plane: Definition, Formula, Examples, FAQs

What Is the Distance between Point and Plane?

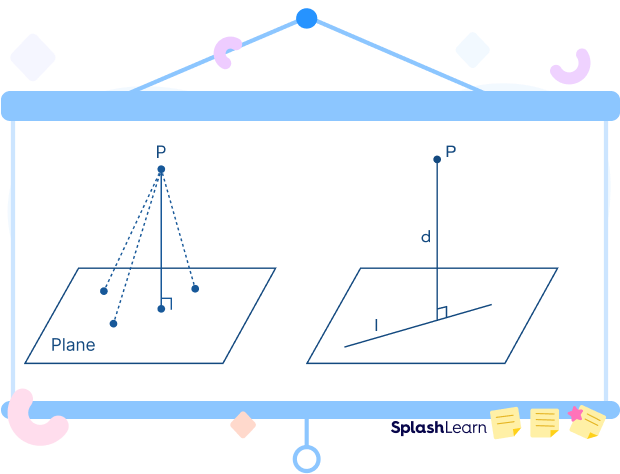
The distance between a point and a plane is equal to the length of the perpendicular drawn to the plane from the given point.

You can draw an infinite number of line segments from a given point to a plane. However, the distance between a point and a plane is the shortest distance possible between the point and the plane.

Formula for Distance between a Point and a Plane

The distance between the point $P(x_{0}, y_{0}, z_{0})$ and the plane with the equation

$Ax + By + Cz + D = 0$ is given by the formula: 

$d =  \frac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} +C^{2}}}$

How to Find the Distance from the Point to the Plane

Now that we know the formula to calculate the shortest distance from point to plane, we simply substitute the values in the formula and simplify.

$d =  \frac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} +C^{2}}}$

Step 1: Write down the values of $x_{0}, y_{0}, z_{0}$ from the coordinates of the point.

Step 2: Write down the values of A, B,C, and D from the equation of plane.

Step 3: To find the value in the numerator, replace the values of x, y, and z in the equation of the plane by by $x_{0}, y_{0}$, and $z_{0}$ respectively. Write the absolute value of the final answer.

Step 4: To find the value in the denominator, find the square root of the sum of squares of A, B, and C. 

Step 5: Simplify.

How to Apply the Distance from Point to Plane Formula

Let’s understand how to find the distance between a point and a plane with the help of an example.

Example: Determine the distance between the point $P = (3, 1, 2)$ and the plane $3x + 4y + z + 3 = 0$.

Step 1: Comparing the coordinates of the point $P = (3, 1, 2)$ with $P = (x_{0}, y_{0}, z_{0})$, we get

 $x_{0} = 3, y_{0} = 1, z_{0} = 2$

Step 2: Comparing the equation of the plane $3x + 4y + z + 3 = 0$ with

$Ax + By + Cz + D = 0$, we get

$A = 3, B = 4, C = 1, D = 3$

Step 3: Substitute the values in the formula and simplify.

We know that the formula for distance between point and plane is

 $d =  \frac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} +C^{2}}}$

Substituting the values in the formula, we get

$d = \frac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} + C^{2}}}$

$d = \frac{|3 \times 3 + 4 \times 1 + 1 \times 2 + 3|}{\sqrt{(9 + 16 + 1)}}$

$d = \frac{|9 + 4 + 2 +  3|}{\sqrt{9 + 16 + 1}}$

$d = \frac{18}{\sqrt{26}}$

$d\;=\;\frac{9\sqrt{26}}{13}$ units

Facts about Distance between Point and Plane

Conclusion

In this article, we learned how to find the distance between a point and the plane, the formula, and application of the formula. Now, let’s solve some practice problems and examples for better understanding.

Solved Examples on Distance Between Point and Plane

1. Find the distance between the point $(\;-\;5, \;-\;8, \;-\;6)$ and the plane $\;-\;2𝑥 + 𝑦 + 2𝑧 = 7$.

Solution:

We know that the formula for distance between point and plane is: 

$d =  \frac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} +C^{2}}}$

Here, $A = \;-\; 2, B = 1, C = 2, D = \;-\;7$, 

$x_{0} = \;-\;5, y_{0} = \;-\;8, z_{0} = \;-\;6$

Substituting the values in the formula, we get

$d =  \frac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} + C^{2}}}$

$d  =  \frac{|\;-\;2 \times \;-\;5 + 1 \times \;-\;8 + 2 \times \;-\;6 + \;-\;7|}{\sqrt{(4 + 1 + 4)}}$

$d  =  \frac{|(10) + (\;-\;8) + (\;-\;1 2) +  \;-\;7|}{\sqrt{9}}$

$d =  \frac{|\;-\;17|}{\sqrt{9}}$

$d = 173$  units

The distance between the point $(\;-\;5, \;-\;8, \;-\;6)$ and the plane $\;-\;2𝑥 + 𝑦 + 2𝑧 = 7$ is 173 units.

2. Find the distance between the point $(2,\; -\;1, 3)$ and the plane $\;-\;2𝑥 + 2𝑦 + 𝑧 = 3$.

Solution: 

We know that the formula for distance between point and plane is:

$d (P,\pi ) =  \frac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} + C^{2}}}$

$(x_{0}, y_{0}, z_{0}) = (2, \;-\;1 ,3)$,

$𝑎  = \;−\;2, 𝑏 = 2, 𝑐 = 1$, and $𝑑 = \;-\;3$

Substituting these values, we get

$𝑑  =  \frac{(\;−\;2)(2) + (2)(\;−\;1) + (1)(3) \;−\; 3}{\sqrt{(4 + 4 + 1)}}$

$𝑑 =  \frac{|(\;-\;4) + (\;-\;2) +(3) +  \;-\;3|}{\sqrt{9}}$

$𝑑 =  \frac{|-6|}{\sqrt{9}}$        

$𝑑 = \frac{6}{3}$

$𝑑 =  2$ units

3. Find the distance from the point (1, 2, 0) to the plane $3x \;-\; 4y \;-\; 5z \;-\; 2 = 0$.

Solution:

We know that the formula for distance between point and plane is:

$d (P,\pi ) =  \frac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} + C^{2}}}$

Here, $A = 3,\; B = \;-\;4,\; C = \;-\;5, D = \;-\;2, x_{0} = 1,\; y_{0} = 2, z_{0} = 0$

Substituting the values in the formula, we get

$d  =  \frac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} + C^{2}}}$

$d =  \frac{|3 \times 1 + (\;−\;4) \times 2 + (\;−\;5) \times 0 \;−\; 2|}{\sqrt{3^{2} + (\;-\;4)^{2} + (\;−\;5)^{2}}}$

$d  =  \frac{|(3) + (\;-\;8) +(0) \;-\;2|}{\sqrt{9 + 16 + 25}}$

$d =  \frac{7}{\sqrt{50}}$

$d = \sqrt{7}{5\sqrt{2}}$  units

 The distance from the point (1, 2, 0) to the plane $3x \;-\; 4y \;-\; 5z \;-\; 2 = 0$ is $\frac{7}{5\sqrt{2}}$  units

Practice Problems on Distance between Point and Plane

Frequently Asked Questions about the Distance between Point and Plane