Distance between Two Points: Introduction
Given any two points on a coordinate plane, we can find the distance between them if the coordinates of both points are known. It is a fundamental concept in geometry. Let’s dive right into it!
Recommended Games
Distance between Two Points: Definition
We can define the distance between two points as the length of the line segment that connects the two given points. Distance between two points on the Cartesian plane can be calculated by finding the length of the line segment that joins the given coordinates.
Recommended Worksheets
What Is the Distance between Two Points?
There is only one line passing through two points. So, the distance between two points can be calculated by finding the length of the line segment connecting the two points.
For example, if P and Q are two points and PQ $= 8$ feet, it means that the distance between the points P and Q is 8 feet.
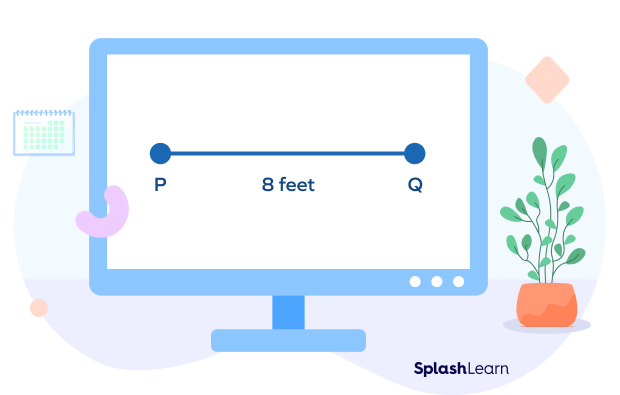
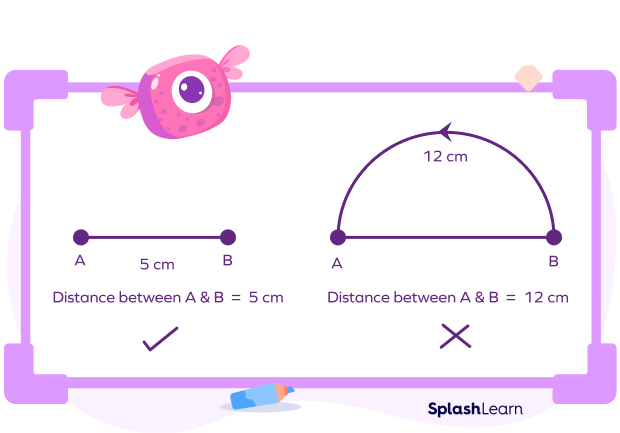
The distance between two points is the length of the line segment joining them. Since the length of the line segment cannot be negative, the distance between two points is always positive.
The distance from the point A to B is the same as the distance from B to A.
NOTE: The shortest distance between two points is the straight line joining them.
What Are the Coordinates of a Point?
In Euclidean geometry, the position of points is defined by their coordinates along the X- axis and Y-axis. Therefore, the coordinates of a point is the ordered pair that is used to identify the location of that point in the coordinate plane.
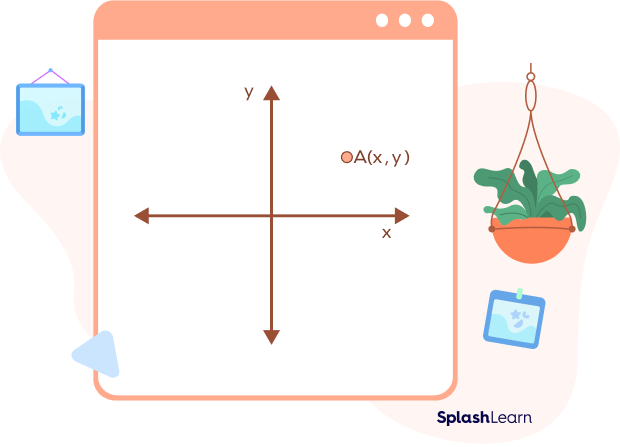
In the above figure, the coordinates of point A are (x,y). This means that the point A is x units away from the y-axis and y units away from the x-axis.
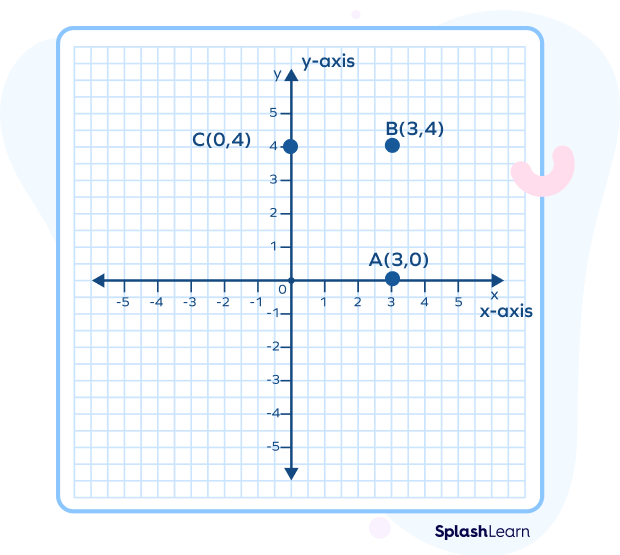
Coordinates of a point on the x-axis are of the form (x, 0), where x is the distance of the point from the origin.
Coordinates of a point on the y-axis are of the form (0, y), where y is the distance of the point from the origin.
How to Find the Distance between Two Points?
To find the distance between two points, we find the distance between two coordinates corresponding to those points using the distance formula. For any point in the 2-D Cartesian plane, we apply the 2-D distance formula or the Euclidean distance formula.
The Distance between Two Points Formula
If the coordinates of the points are P$(\text{x}_{1},\text{y}_{1})$ and Q$(\text{x}_{2},\text{y}_{2})$, then the distance between P and Q is given by
PQ $=\sqrt{(\text{x}_{2} − \text{x}_{1})^{2} + (\text{y}_{2} − \text{y}_{1})^{2}}$
Derivation of Distance Formula
Suppose we have two points A$(\text{x}_{1},\text{y}_{1})$ and B$(\text{x}_{2},\text{y}_{2})$ in the coordinate plane. We have to find the distance between them.
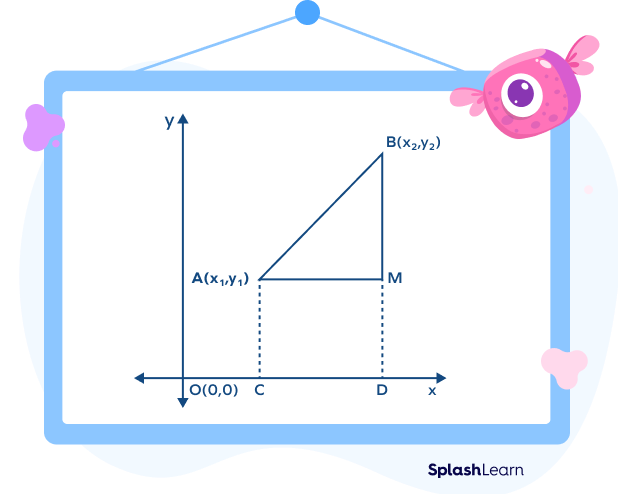
What do we know?
AC and BD are perpendicular to the x-axis.
AB is parallel to the x-axis.
Coordinates: A$(\text{x}_{1},\text{y}_{1})$ and B$(\text{x}_{2},\text{y}_{2})$, $C(\text{x}_{1},0)$ and D$(\text{x}_{2},0)$
Distance between the points A and B is calculated as follows:
C and D are the points on the x-axis.
Here,
$\text{AM} = \text{CD} = \text{OD} – \text{OC} = \text{x}_{2} – \text{x}_{1}$
Similarly, $\text{AC} = \text{MD}$
$\text{AC} = \text{MD} = \text{BD} – \text{AC} = \text{y}_{2} – \text{y}_{1}$
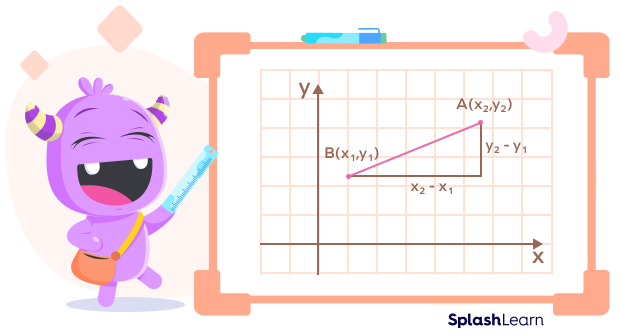
By Pythagoras’ theorem,
$PQ^{2} = PR^{2} + QR^{2}$
PQ $=\sqrt{(\text{x}_{2} − \text{x}_{1})^{2} + (\text{y}_{2} − \text{y}_{1})^{2}}$
Therefore, distance between two points $(\text{x}_{1},\text{y}_{1})$ and $(\text{x}_{2},\text{y}_{2})$ is given by:
PQ $=\sqrt{(\text{x}_{2} − \text{x}_{1})^{2} + (\text{y}_{2} − \text{y}_{1})^{2}}$
The final formula remains the same, irrespective of which quadrants A and B lie in.
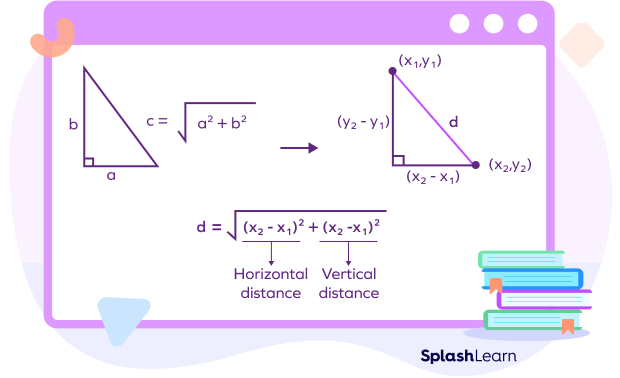
We can summarize the formula in a picture as:
Example 1: The distance between the points P(3, 0) and Q(0, 4) is
PQ $=\sqrt{(4 − 0)^{2} + (0 − 3)^{2}} = \sqrt{16 + 9} = \sqrt{25} = 5$ units
Example 2: R(2, 5) and S(1, 2)
RS $=\sqrt{(1 − 2)^{2}+(2 − 5)^{2}} = \sqrt{1 + 9} = \sqrt{10}$ units
Distance of a Point from the Origin
Suppose a point P(x, y) in the xy–plane as shown in the figure below:
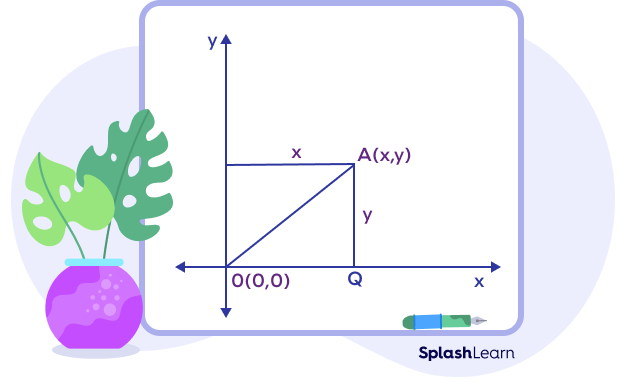
The distance between point A and the origin is OA.
Point A is x units away from the y-axis and y units away from the x-axis.
Using Pythagoras’ theorem, we get
OA $=\sqrt{(x − 0)^{2} + (y − 0)^{2}} = \sqrt{x^{2} + y^{2}}$
Thus, the distance between any point (x,y) in xy-plane and the origin (0,0) is given by: d $= \sqrt{x^{2} + y^{2}}$
Distance between Two Points: Using Pythagoras’ Theorem
Consider the following example.
A boy started from point A and walked west for 12 miles. He then turned to the north and walked for 5 miles more. We have to calculate the shortest distance between the initial position and final position.
A pictorial representation of the above situation is:
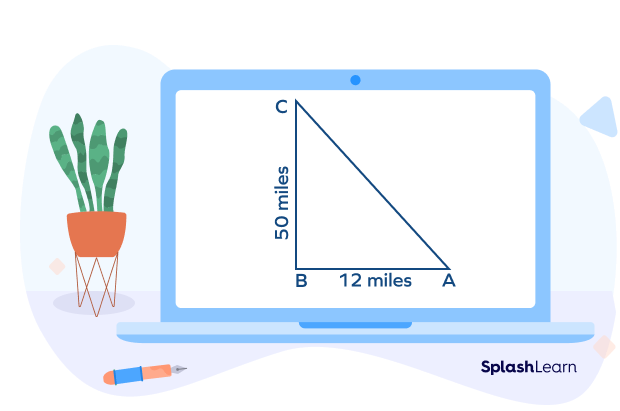
The initial position is A and the final position is C. The distance between points A and B is 12 miles and between points B and C is 5 miles. Here, triangle ABC is a right triangle.
The shortest distance between points A and C is given by AC. This distance is calculated using the Pythagoras theorem as follows:
$AC = \sqrt{AB^{2} + BC^{2}} = \sqrt{12^{2} + 5^{2}} = \sqrt{144 + 25} = \sqrt{169} = 13$ miles
Conclusion
In this article, we learned about the distance between two points. The distance between two points can be calculated by measuring the length of the line segment. To read more such informative articles on other concepts, do visit our website. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.
Solved Examples
1. What is the distance between (0,0) and (3,4)?
Solution: The distance between (0,0) and (x,y) is given by: $\sqrt{x^{2} + y^{2}}$
The distance between (0,0) and (3,4) is given by: $\sqrt{3^{2} + 4^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5$ units.
2. Find the distance between the points $( − 1,2)$ and $(4, − 8)$.
Solution: The distance between the points $( − 1,2) and $(4, − 8)$ is given by:
$\sqrt{(4 − ( − 1))^{2} + ( − 8 − 2)^{2}} =\sqrt{5^{2} + ( − 10)^{2}} = \sqrt{25 + 100} = \sqrt{125} = 5\sqrt{5}$ units
3. If the distance between the points $(4, 4)$ and $(1, a)$ is 5 units, then find the value of a.
Solution: Distance between the points $(4, 4)$ and $(1, a) = \sqrt{(1 − 4)^{2} + (a − 4)^{2}}$
$5 = \sqrt{(1 − 4)^{2} + (a − 4)^{2}} = \sqrt{( − 3)^{2} + (a − 4)^{2}}$
On squaring both the sides, we get the equation for distance between two points as
$25 = 9 + (a − 4)^{2}$
$25 − 9 = (a − 4)^{2}$
$16 = (a − 4)^{2}$
Taking square root
$4 = a − 4$ or $− 4 = a − 4$
$a = 8$ or $a = 0$.
4. Find a point on the x axis that is equidistant from the points $(1,− 4)$ and $( − 3,4)$.
Solution: Let the point on x axis be B$(x,0)$ and let A$(1, − 4)$ and C$( − 3,4)$.
$AB = BC \Rightarrow AB^{2} = BC^{2}$
$(x − 1)^{2} + (0 −(− 4))^{2} =(x −( −3))^{2} + (0 − 4)^{2}$
$(x −1)^{2} + 16 = (x + 3)^{2} + 16$
$(x − 1)^{2} − (x + 3)^{2} = 16 − 16$
$x^{2} − 2x + 1 − (x^{2} + 6x + 9) = 0$
$x^{2} − 2x + 1 − 9 − x^{2} − 6x = 0$
$− 8x − 8 = 0$
$− 8x = 8$
$x = \frac{−8}{8} = −1$
The point is $( −1,0)$.
5. Amaya traveled 20 miles to the west and then 21 miles to the north. Calculate the shortest distance between the initial and final point?
Solution: Assuming $AB = 20$ mi and $BC = 21$ mi
The shortest distance $= AC =$
$= \sqrt{AB^{2} + BC^{2}} = \sqrt{20^{2} + 21^{2}} = \sqrt{400 + 441} = \sqrt{841} = 29$ mi
Practice Problems
Distance Between Two Points
If the distance between the origin and $(a, 8)$ is 17 units, then find the value of $a$.
The distance between $(0,0)$ and $(a, 8)$ is given by: $\sqrt{a^{2} + 8^{2}} = 17$
On squaring, we get $a^{2} + 64 = 289$
$\Rightarrow a^{2} = 289$ $-$ $64 \Rightarrow a^{2} = 225 \Rightarrow a = 15$
The distance of $(-$$5,8)$ from x-axis is:
The distance of $(-$$5,8)$ from x-axis is the distance between $(-$$5,8)$ and $(-$$5,0)$.
The distance of $(-$$5,8)$ from x-axis $= |8$$-$$0| = 8$ units.
The distance of $(-$$2,-$$10)$ from y-axis is:
The distance of $(-$$2,-$$10)$ from y-axis $= | -2|$ units $= 2$ units
Find half the length of the line segment joining the points $(2,3)$ and $(5,7)$.
The distance between the points $(2,3)$ and $(5,7)$ is
$\sqrt{(5 - 2)^{2} + (7 - 3)^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5$ units. Half the distance is 2.5 units.
Shyna traveled east by bus and west by car. If the distance covered by bus is 24 km and the shortest distance is 25 km, then what is the distance covered by car?
Let the distance covered by car be $x$ km.
Shortest distance $= \sqrt{24^{2} + x^{2}} \Rightarrow 25 = \sqrt{24^{2} + x^{2}}$
Squaring both the sides, we get $625 = 576 + x^{2} \Rightarrow x^{2} = 49 \Rightarrow x = 7$
Frequently Asked Questions
What is the distance between two points in a 3D plane?
If the coordinates of two points in a 3D plane are P$(\text{x}_{1}, \text{y}_{1}, \text{z}_{1})$ and Q$(\text{x}_{2}, \text{y}_{2}, \text{z}_{2})$, the distance between the points P and Q is given by PQ $= \sqrt{(x_{2} − x_{1})^{2} + (y_{2} − y_{1})^{2} + (z_{2} − z_{1})^{2}}$
What is the shortest distance between two points?
The shortest distance between two points is the length of the straight line that connects both the points. We use the distance formula to find this distance using the coordinates given in a two-dimensional plane.
How can one find the vertical distance between two points?
The vertical distance between two points is calculated by the difference of the y coordinates of the two points, i.e., vertical distance between two points, $|(y_{2} − y_{1})|$.
How to find the horizontal distance between two points?
The vertical distance between two points is calculated by the difference of the y coordinates of the two points, i.e., vertical distance between two points, $(\text{y}_{2} − \text{y}_{1})$ where $(\text{x}_{1}, \text{y}_{1})$ and $(\text{x}_{2},\text{y}_{2})$ are the coordinates of the points.
Can we change the order of the points in the distance formula?
Yes, we can change the order of points in the distance formula. We can also write the formula as $\sqrt{(x_{1} − x_{2})^{2} + (y_{1} − y_{2})^{2}} = \sqrt{(x_{2} − x_{1})^{2} + (y_{2} − y_{1})^{2}}$.
What is the driving distance between two points or places?
The driving distance generally refers to the distance when traveling by car. For example, the driving distance from Chicago to Orlando (is 1179 miles.




































