Distance between Point and Line: Formula, Definition, Examples

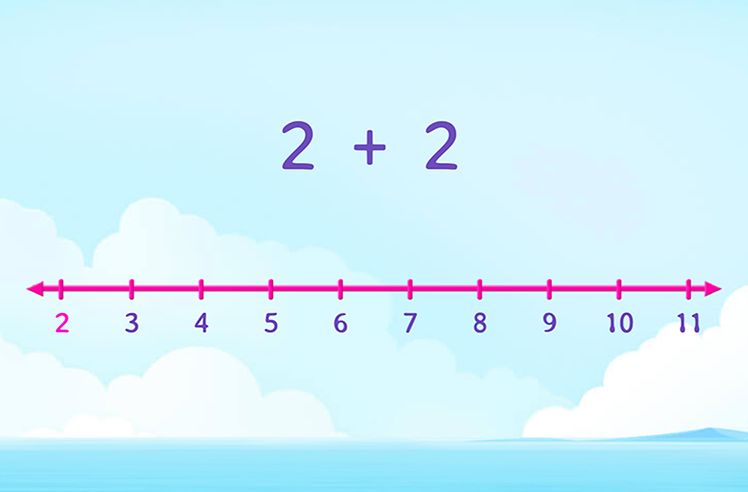
What Is the Distance between a Point and a Line?

The distance between point and line is the shortest distance between the point and the straight line. 

Consider a line BF and a point A as shown in the diagram below. We can draw an infinite number of line segments from the line to the point A. So, what is the actual distance between the given line and the point A?

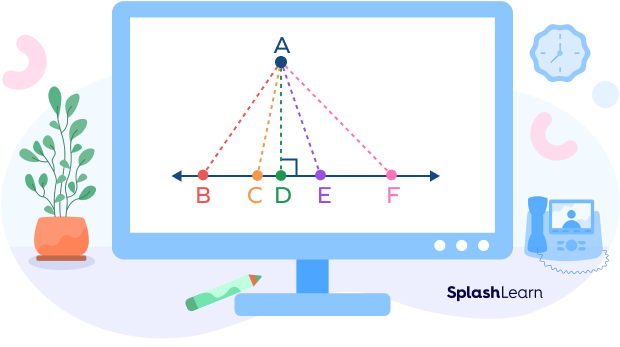
It is the shortest distance from A to the line. How can we find this shortest distance? The shortest distance from a point and a line is the length of the perpendicular drawn from the point to the line. Thus, the line segment AD defines the distance between the point and a line. 

Distance from a Point to a Line Definition in Geometry

The distance between point and line is the shortest distance between the point and a point on the line. The length of a perpendicular drawn from a point to a point on the line defines the shortest distance between them. 

Distance from Point to Line Formula

The distance between point and line for a line $Ax + By + C = 0$ and a point with the coordinates $(x₀, y₀)$ is calculated by the following formula 

$d = \frac{| Ax₀ + By₀ + C |}{\sqrt{A² + B²}}$

where,

A, B, and C are real numbers.

A and B cannot be equal to zero.

The formula has an absolute zero or modulus sign in the numerator which indicates that the value of the numerator would always be a positive number or zero.

How to Find the Distance Between Point and Line

Step 1: Compare the given equation of a line with the standard equation $Ax + By + C = 0$ to find the values of A, B, and C.

Step 2: Compare the coordinates of the given point with $(x₁, y₁)$ to find the values of $x₁$ and $y₁$.

Step 3: Substitute the values in the formula

$d = Ax₁ + By₁ + CA² + B²$

Perpendicular Distance from Point to Line

The shortest distance between point and line is calculated by finding the length of the perpendicular drawn from the point to the line. 

Consider the line l: $Ax + By + C = 0$ and point $P(x₁, y₁)$.

Note that PQ is the perpendicular from point P to line l. Let l$(PQ) = d$.

M and N are the points of intersection of the line on the x-axis and y-axis. 

M is the y-intercept of line l. Putting $x = 0$ in $Ax + By + C = 0$, we get $y = \;-\;\frac{C}{B}$. 

Thus, $M \equiv (0, \;-\;\frac{C}{B})$

N is the x-intercept of line l. Putting $y = 0$ in $Ax + By + C = 0$, we get $x = \;-\;\frac{C}{A}$.

Thus, $N \equiv (\;-\;\frac{C}{A},\; 0)$.

Here, PQ is the height of the  triangle PMN. We use the formula of area of triangle and the distance formula to derive the formula for perpendicular distance between point and line. 

Derivation of the Distance from Point to Line

We have 

l: $Ax + By + C = 0$ and $P(x₁,\; y₁)$

$M \equiv (0,\; -\;\frac{C}{B})$

$N \equiv (\;-\;\frac{C}{A},\; 0)$

To find: distance between point P and line l, which is defined by the length d or length(PQ)

As mentioned earlier, PQ is the height of the $\Delta PMN$.

The formula for the area of a triangle is given by

Area of triangle $= \frac{1}{2} \times$base $\times$ height

Area of PMN $= \frac{1}{2}\times$ MN $\times$ PQ

$\Rightarrow PQ =  \frac{Area\; of\; \Delta PMN \times 2}{AB}$  ———— (i)

Let’s find these two values on the R.H.S.

According to coordinate geometry, the area of PMN can be given as 

$Area of \Delta PMN = \frac{1}{2} |x₁(y₂\;-\;y₃) + x₂(y₃\;-\;y₁) + x₃( y₁\;-\;y₂)|$

$= \frac{1}{2} |x₁(0\;-\;(\;-\;\frac{C}{B})) + (\;-\;\frac{C}{A})((\;-\;\frac{C}{B})\;-\;y₁) +0( y₁\;-\; 0)$

$= \frac{1}{2} | \frac{x₁C}{B} +(\frac{-C}{A})(\frac{-C \;-\; By₁}{B})|$

$= \frac{1}{2} | \frac{x₁C}{B} + (\frac{C²}{AB} + \frac{BCy₁}{AB})|$

$= \frac{1}{2} |\frac{x₁C}{B} + \frac{Cy₁}{A} + \frac{C²A}{B})|$

$= \frac{1}{2}| C(\frac{x₁}{B} + \frac{y₁}{A} + \frac{C}{AB})|$ ————- (ii)

Multiple and divide the equation (ii) by AB 

$Area\; of\; \Delta PMN = \frac{1}{2} |C(\frac{ABx₁}{AB²} + \frac{ABy₁}{A²B} + \frac{ABC}{A²B²})|$

$= \frac{1}{2} |\frac{CAx₁}{AB} + \frac{CBy₁}{AB} + \frac{C²}{AB})|$

$= \frac{1}{2} |\frac{C}{AB}| (Ax₁ + By₁ + C)$ ————– (iii)

Next, the distance of the line AB with coordinates $M(x₁,\; y₁)$ and $N(x₂,\; y₂)$ can be given by distance formula as  $MN = \sqrt{((x₂ \;-\; x₁)²+ (y₂ \;-\;y₁)²)}$

In our case, $M(x₁,\; y₁) = (0,\; -\;\frac{C}{B})$ and $N(x₂,\; y₂) = (\;-\;\frac{C}{A},\; 0)$

$MN = \sqrt{((\;-\;\frac{C}{A}) \;-\; 0)² + (0 \;-\; (\;-\;CB))²)}$

$MN = \sqrt{(\;-\;CA)² + (CB)²)}$

$MN = |\frac{C}{AB}| (A² + B² )$ ————- (iv)

Substituting equations (ii) and (iv) in equation (i) 

$PQ = \frac{1}{2} \times \frac{|\frac{CA}{B}| (Ax₁ + By₁ + C) \times 2}{|\frac{C}{AB}| (\sqrt{A²+ B²})$

$PQ = d = \frac{|(Ax₁ + By₁ + C)|}{\sqrt{A² + B²}}$

Hence, we get that the distance between a point $(x₁,\; y₁)$ and a line $Ax + By + C = 0$ is given 

$d = \frac{|(Ax₁ + By₁ + C)|}{\sqrt{A² + B²}}$

Facts about the Distance between Point and Line

• The distance between a point and a line can never be negative. 
• The formula for distance between point and line has many practical applications in map navigation, construction, and sports.
• The distance between origin and a line $Ax + By + C = 0$ is $d = \frac{|C|}{\sqrt{A² + B²}}$.

Conclusion

The distance between point and line is a basic yet essential concept in coordinate geometry. We learned about the formula for finding the distance between a point and a line along with its derivation. Let’s solve a few examples.

Solved Examples on Distance between Point and Line

Example 1: Find the distance between the point (0, 0) and the line $4x \;-\; 3y + 25 = 0$. 

Solution:

We have $P(x₁,\; y₁) = (0, 0)$ and the line $4x \;-\; 3y + 25 = 0$

$x₁ = 0$ and $y₁  = 0$

$A = 4,\; B = \;-\;3,\; C = 25$

Using the formula for distance between point and line,

$d = \frac{|(Ax₁ + By₁ + C)|}{\sqrt{A² + B²}}$

$d = \frac{(4 \times 0) + (\;-\;3 \times 0)+ 25|}{sqrt{4² + (\;-\;3)²}}$ 

$d = \frac{|0 + 0 + 25|}{\sqrt{16 + 9}}$

$d = \frac{25}{\sqrt{16 + 9}}$

$d = \frac{25}{\sqrt{25}}$ 

$d = \frac{25}{5}$

$d = 5$ units

Example 2: Find the distance between the point $(4,\; 6)$ and line $y = \frac{1}{3}x \;-\; 3$.

Solution:

$(4,\; 6) = (x₁,\; y₁)$

$x₁ = 4,\; y₁ = 6$

$y = \frac{1}{3}x \;-\; 3$

Add 3 on both sides of the equation.

$y + 3 = \frac{1}{3}x \;-\; 3 + 3$

$y + 3 = \frac{1}{3}x$ 

$\frac{1}{3}x \;-\; y + 3 = 0$

Multiply both sides of the equation by 3

$x \;-\; 3y + 9 = 0$ ———- (i)

Comparing equation (i) with $Ax + By + C = 0$, we get

$A = 1,\; B = \;-\;3,\; C = 9$

Using the formula for distance between point and line 

$d = \frac{|(Ax₁ + By₁ + C)|}{\sqrt{A² + B²}}$

$d = \frac{|(1 \times4) + (\;-\;3 \times 6) + 9|}{\sqrt{(\;-\;1)² + (3)²}}$ 

$d = \frac{|4 \;-\; 18 + 9|}{1 + 9}$

$d = \frac{|\;-\;18 + 13|}{\sqrt{10}}$

$d = \frac{5}{\sqrt{10}}$   

$d = \frac{5}{\sqrt{10}}$  units

Example 3: Find the distance between point P(6, 9) and line $2x \;-\; 5y + 7 = 0$.

Solution:

$P(6,\; 9): x1 = 6,\; y1 = 9$

Comparing equation (i) with $Ax + By + C = 0$, we get

$A = 2,\; B = \;-\;5, C = 7$

Using the formula for distance between point and line 

$d = \frac{|(Ax₁ + By₁ + C)|}{\sqrt{A² + B²}}$

$d = \frac{|(2 \times 6) + (- 5 \times 9) + 7|}{\sqrt{(2)² + (\;-\;5)²}}$

$d = \frac{|12 – 45 + 7|}{\sqrt{4 + 25}}$

$d = \frac{|\;-\;45 + 19|}{\sqrt{29}}$

$d = \frac{|\;-\;26|}{\sqrt{29}}$ 

$d = \frac{26}{\sqrt{29}}$ 

$d = \frac{26}{\sqrt{29}}$  units

Practice Problems on Distance Between Point and Line

Frequently Asked Questions on the Distance between Point and Line