What Are Divisibility Rules?
Divisibility rules are simple tips and tricks that are used to check or test whether a number is divisible by another number.
Consider an example. Imagine that you have 13 candy bars. Can you divide them equally among 3 friends? How would you check? You can check if 13 is “divisible by” 3. In other words, you can check if 13 appears in the times table of 3 or not!
What if you wish to check if you can divide 221 candies equally among 6 friends? Finding 221 in the multiplication table of 6 can be very time-consuming. When dealing with large numbers, we need to take a different approach. What do you think?
To solve problems like these in no time, we use divisibility rules. With divisibility rules at your fingertips, you can answer easily without doing too much calculation!
Divisibility Rules: Definition
Divisibility rules are a set of general rules that are often used to determine whether or not a number is absolutely divisible by another number. Note that “divisible by” means a number divides the given number without any remainder, and the answer is a whole number.
Recommended Worksheets
Divisibility Test (Division Rules in Math)
Mathematical tests for divisibility or division rules help you employ a quick check to determine whether a number will be totally divisible by another number.
What are the divisibility rules? Let’s learn divisibility rules 1-13.
Divisibility Rule of 1
Every number ever is divisible by 1.
Divisibility Rule of 2
Every even number is divisible by 2. Any number that ends with 2, 4, 6, 8, or 0 gives 0 as the remainder when divided by 2.
For example, 12, 46, and 780 are all divisible by 2.
Divisibility Rules of 3
A number is completely divisible by 3 if the sum of its digits is divisible by 3. You can also repeat this rule until you get a single-digit sum.
Example 1: Check whether 93 is divisible by 3 or not.
Sum of the digits = 9 + 3 = 12
If the sum is a multiple of 3, then the original number is also divisible by 3.
Here, as 12 is divisible by 3, 93 is also divisible by 3.
Example 2: 45,609
To make the process even easier, you can also find the sum of the digits until you get a single digit.
Sum of digits = 4 + 5 + 6 + 9 + 0 = 24
Adding further, we get 2 + 4 = 6
6 is divisible by 3.
Thus, 45609 is divisible by 3.
Divisibility Rule of 4
If the number formed by the last two digits of a number is divisible by 4, then that number is divisible by 4. Numbers having 00 as their last digits are also divisible by 4.
Example 1: Consider the number 284. Check the last two digits.
The last two digits of the number form the number 84. As 84 is divisible by 4, the original number 284 is also divisible by 4.
Example 2: 1328

The number formed by the last 2 digits is 28.
28 is divisible by 4.
Thus, 1328 is also divisible by 4.
Divisibility Rule of 5
If a number ends with 0 or 5, it is divisible by 5.
For example, 35, 790, and 55 are all divisible by 5.
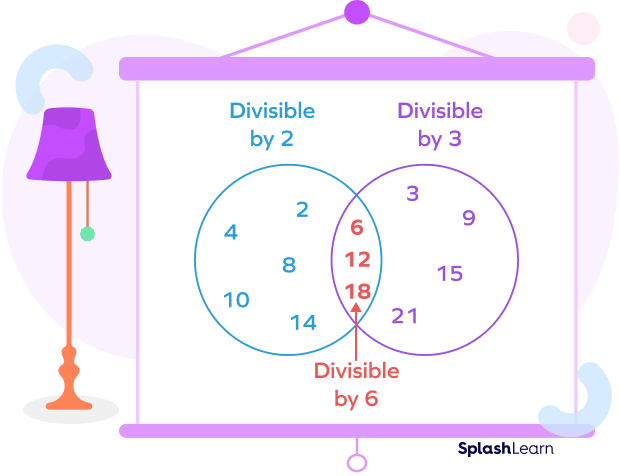
Divisibility Rule of 6
If a number is divisible by 2 and 3, it will be divisible by 6 as well.
For example, the numbers 6, 12, and 18 are divisible by 2 and 3. So, they are divisible by 6 as well.
Divisibility Rules of 7
If subtracting twice of the last digit from the number formed by remaining digits is 0 or divisible by 7, the number is divisible by 7. This one is a little tricky. Let’s understand with an example.
Example: Check whether 905 is divisible by 7 or not.
Step 1: Check the last digit and double it.
Last digit $= 5$
Multiply it by 2.
$5 \times 2 = 10$
Step 2: Subtract this product from the rest of the number.
Here, the remaining number $= 90$
$90 \;-\; 10 = 80$
Step 3: If this number is 0 or a multiple of 7, then the original number is also divisible by 7.
80 is not divisible by 7. So, 905 is also not divisible by 7.
Divisibility Rule of 8
If the number formed by the last three digits of a number is divisible by 8, we say that the number is divisible by 8.
Example 1: In the number 4176, the last 3 digits are 176.
If we divide 176 by 8, we get:
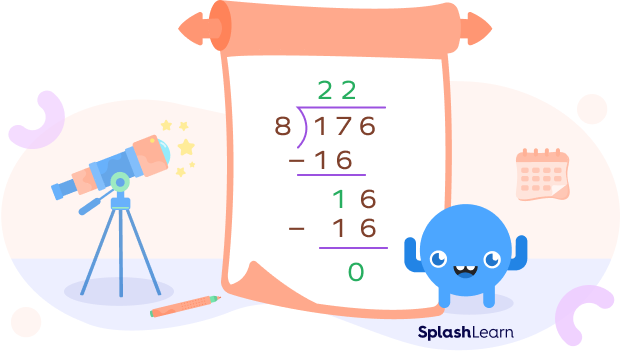
Since 176 is divisible by 8, 4176 is also divisible by 8.
Example 2:

Thus, 12,920 is divisible by 8.
Divisibility Rule of 9
If the sum of digits of the number is divisible by 9, then the number itself is divisible by 9. You can keep adding further by repeating the rule. If the single-digit sum is 9, the number is divisible by 9.
Example 1: Consider 189.
The sum of its digits$ = (1+8+9) = 18$, which is divisible by 9, hence 189 is divisible by 9.
Example 2: 12,897
Sum of digits $= 1 + 2 + 8 + 9 + 7 = 27$
Adding further, $2 + 7 = 9$
Thus, 12897 is divisible by 9.
Divisibility Rule of 10
Any number whose last digit is 0 is divisible by 10.
Example: 10, 20, 30, 100, 2000, 40,000, etc.
Divisibility Rule for 11
If the difference of the sum of alternative digits of a number is divisible by 11, then that number is divisible by 11.
Example 1: Consider the number. 2846767. First, understand the digit positions. We find two sums: the sum of digits at the even places and the sum of digits at the odd places.
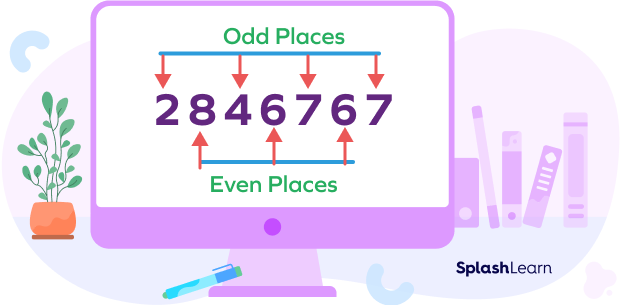
Sum of digits at even places (From right) $= 8 + 6 + 6 = 20$
Sum of digits at odd places (From right) $= 7 + 7 + 4 + 2 = 20$
Difference $= 20 – 20 = 0$
Difference is divisible by 11.
Thus, 2846767 is divisible by 11.
Example 2: Is 61809 divisible by 11?
Identify digits in odd places and digits in even places.

Here, $6 + 8 + 9 = 23$ and $0 + 1 = 1$
Difference $= 23 – 1 = 22$
22 is divisible by 11.
Thus, the given number is divisible by 11.
Another Divisibility Rule For 11
There’s another simple divisibility rule for 11.
Subtract the last digits from the remaining number. Keep doing this until we get a two-digit number. If the number obtained is divisible by 11, the original number is divisible by 11.
Example: 1749
$174\;-\;9 = 165$
$16\;-\;5 = 11$ … divisible by 11
Thus, 1749 is divisible by 11.
Divisibility Rule of 12
If the number is divisible by both 3 and 4, then the number is divisible by 12
Example: 4880
Sum of the digits $= 4 + 8 + 8 + 0 = 20$ (not a multiple of 3)
Last two digits $= 80$ (divisible by 4)
The given number 4880 is divisible by 4 but not by 3.
Thus, 4880 is not divisible by 12.
Divisibility Rules of 13
To check if it is divisible by 13, we add 4 times of the last digit of the remaining number and repeat the process until we get a two-digit number. If that two-digit number is divisible by 13, then the given number is divisible by 13.
Example: Is 4186 divisible by 13?
- $418 + (6 \times 4) = 418 + 24 = 442$
- $44 + (2 \times 4) = 44 + 8 = 52$
52 is divisible by 13 since $13 \times 4 = 52$.
Thus, 4186 is divisible by 13.
Divisibility Rules: Chart
| Divisibility Rules Chart | |
|---|---|
| Divisibility by 1 | Every number is divisible by 1. |
| Divisibility by 2 | When the last digit is 0, 2, 4, 6, or 8 |
| Divisibility by 3 | When the sum of digits is divisible by 3 |
| Divisibility by 4 | When the last two digits of any dividend are divisible by 4 (NOTE: Numbers having 00 as their last digits are also divisible by 4.) |
| Divisibility by 5 | When the last digit is either 0 or 5 |
| Divisibility by 6 | When the number is divisible by both 2 and 3 |
| Divisibility by 7 | When the last digit is subtracted twice from the remaining digits and gives the multiple of 7 |
| Divisibility by 8 | When the last three digits are divisible by 8(NOTE: Numbers having 000 as their last digits are also divisible by 8.) |
| Divisibility by 9 | When the sum of all digits is divisible by 9 |
| Divisibility by 10 | When the last digit is 0 |
| Divisibility by 11 | When the difference between the sums of the alternative digits is divisible by 11 |
| Divisibility by 12 | When a number is both divisible by 3 and 4 |
| Divisibility by 13 | Multiply 4 with the last digit and add this product to the remaining number. Continue till a two-digit number is found. If the 2-digit number is divisible by 13, the number is divisible by 13. |
Facts about Divisibility Rules
- “Divisible” means a number can be divided evenly with another number with NO remainders.
- The divisibility rule is a shortcut to analyze whether an integer is completely divisible by a number without actually doing the calculation.
- Zero is divisible by any number (except by itself), so it gets a “yes” to all these tests.
- When a number is divisible by another number, it is also divisible by each of the factors of that number. For instance, a number divisible by 6 will also be divisible by 2 and 3. A number divisible by 10 is also divisible by 5 and 2.
- Numbers that have two zeros at the end are divisible by 4. Numbers with three zeros at the end are divisible by 8.
- The number 2,520 is the smallest number that is divisible by 2, 3, 4, 5, 6, 7, 8, 9, and 10.
Conclusion
In this article, we have learned divisibility rules and charts with examples. Let’s solve some divisibility rules examples to understand it better.
Solved Examples for Divisibility Rules
1. If a number is divisible by 6, can we say it is divisible by 2 as well?
Solution:
Yes, because 6 is divisible by 2.
If a number is divisible by some numbers, say x, that number is also divisible by factors of x.
For example, 480 is divisible by 6.
Thus, $480 \div 6 = 80$.
$480 \div 2 = 240$.
Also, $480 \div 3 = 160$
Thus, If a number is divisible by 6, can we say it is divisible by 2 and 3 as well, as 2 and 3 are factors of 6.
2. Use divisibility rules to check whether 642 is divisible by 4 and 3.
Solution:
Divisibility rule for 4: If the last two digits of a number are divisible by 4, then that number is divisible by 4.
The last two digits of $642 = 42$, which is not divisible by 4.
Thus, 542 is not divisible by 4.
Divisibility rule of 3: If the sum of digits is divisible by 3, we say that the original number is divisible by 3.
Sum of digits $= 6 + 4 + 2 = 12$
12 is divisible by 3.
So, 542 is not divisible by 8.
3. Check 3640 for divisibility by 13.
Solution:
The last number of the given number is 0.
Multiply 4 by 0 and add to the rest of the number.
$364 + (0 \times 4) = 364$.
Again, multiply 4 by the last digit of the obtained three-digit number and add to the rest of the digits as
$36 + (4 \times 4) = 52$
Now, we obtained a two-digit number 52, which is divisible by 13.
$52 = 4 \times 13$
Hence, 3640 is divisible by 13.
Rules of Divisibility: Definition, Chart, Examples
Which number is not divisible by 5?
According to the divisibility rule of 5, If the last digit of a number is 5 or 0, the number is always divisible by 5. So, 680 is divisible by 5.
Which of the following numbers is divisible by 2?
All even numbers are divisible by 2.
Which of the following numbers is divisible by 6?
According to the rule of divisibility by 6, the number divisible by both 2 and 3 is also divisible by 6. In the given list, only 18 is divisible by 2 and 3. Thus, 18 is divisible by 6.
Identify a number divisible by 9.
Sum of digits in the number $117 = 1 + 1 + 7 = 9$.
The sum is divisible by 9. Thus, 117 is divisible by 9.
For all the other options, the sum of digits in a number is not divisible by 9.
Frequently Asked Questions on Divisibility Rules
What are co-primes and their divisibility rules?
Co-primes are a pair of numbers that have 1 as the common factor. If the number is divisible by such co-primes, the number is also a divisible by-product of the co-primes. For example, 14 is divisible by both 2 and 7. They are co-primes that have only 1 as the common factor, so the number is divided by 14, the product of 2 and 7.
When is a number said to be a factor of another number?
A number x is said to be a factor of number y if y is divisible by x. For example, 10 is divisible by 2, so 2 is a factor of 10.
Where do we use divisibility rules in real life?
Divisibility rules are the quickest way to determine if a number is divisible by another number. It saves the time required to perform the actual division. Divisibility rules also give you a number sense when it comes to division and multiplication of two or more numbers.
What are composite numbers?
In math, composite numbers can be defined as numbers that have more than two factors. Numbers that are not prime are composite numbers because they are divisible by more than two numbers.
For example:
Factors of $4 = 1, 2, 4$, i.e.,
Since 4 has more than two factors, 4 is a composite number.
How many divisibility rules are there?
We often have standards for divisibility from 1 to 20. However, if we were able to recognize the pattern of multiples of integers, we could develop further tests for divisibility. For example, the divisibility rule of 21 states that a number must be divisible by both 3 and 7. It is because 21 is a multiple of two prime numbers 3 and 7, so all the multiples of 21 will definitely have 3 and 7 as their common factors.

























