Partitive Division: Introduction
Partitive division is a type of a division problem in which we divide a number into a known number of groups.
We know that division is breaking down a large group of items into smaller groups such that each group has an equal number of items. It is one of the four fundamental operations in mathematics and results in an equal distribution of resources.
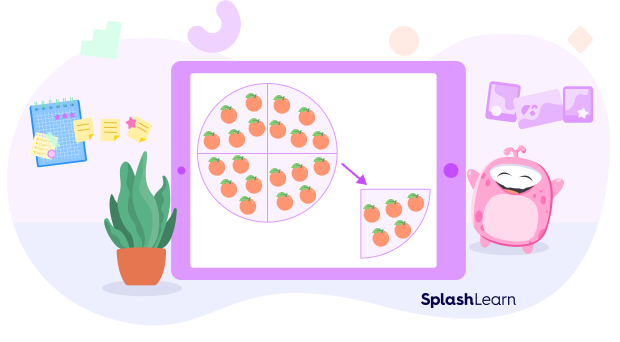
Suppose you wish to divide 20 oranges equally among 4 groups. It’s a partitive model of division, since the number of groups is known.
Recommended Games
What is Partitive Division?
A partitive division problem is one where you know the total number of groups, and are trying to find the number of items in each group. Partition division—sometimes referred to as sharing, partitive, and grouping division—is a method of dividing a sum into the same amount of groups. If you divide in this fashion, then 284 signifies that there are 28 items evenly distributed across 4 groups.
Recommended Worksheets
Partitive Division Definition
Partitive division can be defined as a division problem in which the number is to be divided into the given number of groups, and we have to find the number of items that get assigned to each group.
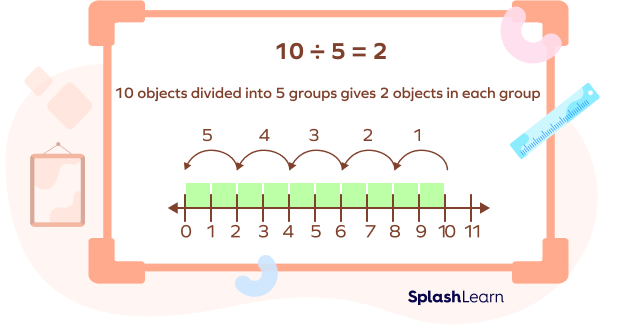
Understanding Partitive Division Using Number Line
Let’s divide 10 items equally into 5 groups. So, we will divide 10 by 5. If we divide the segment joining 0 and 10 into 5 equal “partitions” or 5 equal groups, each group will have 2 numbers.
Here, we know the number of groups and we find the number of items in each group.
Partitive Division Using Repeated Subtraction
Let’s understand how to solve a partitive division word problems using repeated subtraction.
Suppose 24 flowers are to be equally distributed among 8 vases, how many flowers would there be in each vase? This is a partitive division problem. Let us see how we can find the answer to this question.
Here, we have 24 flowers and 8 groups. Eight vases hold eight equal arrangements of 24 flowers.
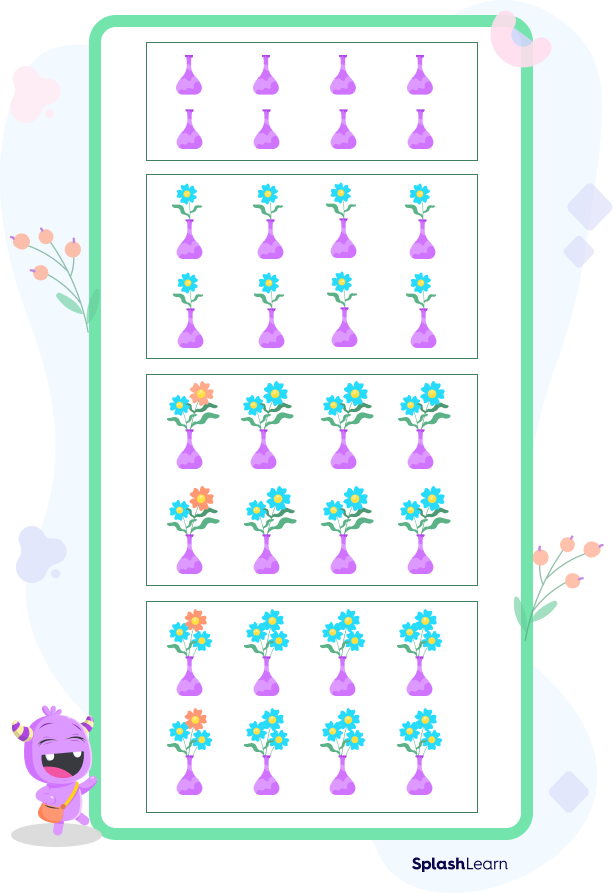
Place 1 flower in each group to begin.
We divided the eight flowers into eight groups, putting one flower in each.
Thus, $24 – 8 = 16$ flowers are left.
Put 1 flower in each group once again.
We have now added 8 more flowers to the 8 groups.
$16 – 8 = 8$ flowers are still available.
Put 1 flower in each group once more.
We have $8 – 8 = 0$ flowers remaining after arranging the final 8 flowers in the final 8 groups. Each group contains 3 flowers.
We can summarize the repeated subtraction as subtracting the number of groups from the total number of items until we get remainder 0.
$24 – 8 = 16$
$16 – 8 = 8$
$ 8 – 8 = 0$
Solving Partitive Division Problems Using Long Division
To find the number of items in each group, we can directly divide the total number of items (dividend) by the total number of groups (divisor). The quotient obtained is the number of items in each group. Some helpful definitions are:
Dividend: A number to be divided by another number.
It represents the total number of items.
Divisor: A number by which another number is to be divided.
It represents the number of groups.
Quotient: The result obtained by dividing one number by another number.
It represents the number of items in each group.
Remainder: The number left after division.
It represents the number of items left.
Example: If we divide 32 fruits equally in 8 bags, each bag will have 4 fruits.

Fun Fact!
The word “partitive” comes from “partition” where the number of items (dividend) is equally partitioned (shared or distributed) into the given number of groups (divisor). Then, we can find the number of items in each group.
Conclusion
Partitive division problems provide the total number of objects and the number of groups into which the objects should be divided. Let’s solve a few partitive division examples and practice problems.
Solved Examples
1. Suppose, there are 48 candies equally distributed in 12 boxes. Find how many candies are in each box using repeated subtraction.
Solution:
Number of candies $= 48$
Number of boxes $=$ Number of groups $= 12$
Let’s use repeated subtraction to solve this problem. Subtract the number of boxes from the total number of candies until we get remainder 0.
Step 1: $48 – 12 = 36$
Step 2: $36 – 12 = 24$
Step 3: $24 – 12 = 12$
Step 4: $12 – 12 = 0$
We subtracted 12 four times to get 0 remainder. So, each box will have 4 candies.
2. Use the long division method to find how many roses each gift basket will contain if there are 100 roses and 4 gift baskets.
Solution:
Number of roses $= 100$
Number of gift baskets $= 4$
Number of roses in each gift basket $= 100 \div 4$
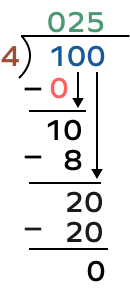
Quotient $= 25$
So, there will be 25 roses in each gift basket.
3. Jesse divides his study hours equally among 3 subjects. If he studies for 9 hours every day, how many hours does he dedicate to each subject? State whether this is a partitive division problem or not. Explain why or why not and solve the problem.
Solution:
Number of study hours $= 9$ hours
Number of subjects $= 3$
In a partitive division problem, the number of groups are known and we have to find the number of items in each group.
Here, the number of subjects represents the number of groups. We have to distribute 9 hours equally into 3 groups. Thus, this is a partitive division problem.
The number of hours dedicated to each subject $= 9 \div 3 = 3$ hours
So, Jesse dedicates 3 hours to each subject.
Practice Problems
Partitive Division
There are 24 apples equally divided into 6 baskets. Find how many apples are in each basket using division.
Total number of apples $= 24$
Number of baskets $= 6$
Number of apples in each basket $= 24 \div 6 = 4$
At a restaurant, a $\$44$ bill is to be divided among 4 friends. What will be each friend’s share?
This is a partitive problem.
Total bill amount $= \$44$
Number of friends $= 4$
Share of each friend $= 44 \div 4 = 11$
40 balls are packed equally in 5 boxes. What is the quotient?
When 40 is divided by 5, we get
$40 5 = 8$
So, the quotient is 8. It means that 8 balls are packed in each box.
Frequently Asked Questions
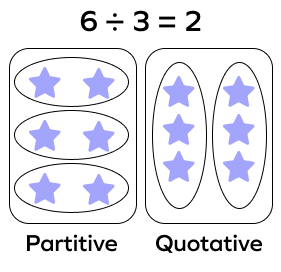
What is quotative division?
In quotative division, we divide a number into groups of a measured quantity. So, we know the number of items in each group and we find the number of groups.
When do we use partitive division in real life?
In the partitive division problems, the number of groups are known and we have to find the number of items in each group. So, whenever we have to divide an item or an amount into equal groups, we use partitive division. Examples: Dividing expenses or bills, planning household budgets, distributing things or goods equally among people, managing time for different tasks, etc.
When do we use quotative division?
We use quotative division when the total number of items in each group is known and we have to find the number of groups. Here, we divide the total number of items by the number of items in each group.




































