What is a Dodecagon?
A polygon is a two-dimensional closed geometric figure with a finite number of sides. The sides of a polygon are made of line segments. We need a minimum of three line segments to make a polygon. You may have come across polygons in your daily routine. Polygons like triangles, quadrilaterals, and more. One such type of polygon is a dodecagon with 12 sides. And in this article, we shall explore the definition of dodecagon and more.
Definition of Dodecagon
In geometry, a 12-sided polygon is called a dodecagon. It also has twelve vertices and twelve interior angles. Let’s take a look at some of the examples of dodecagon in the figure below.
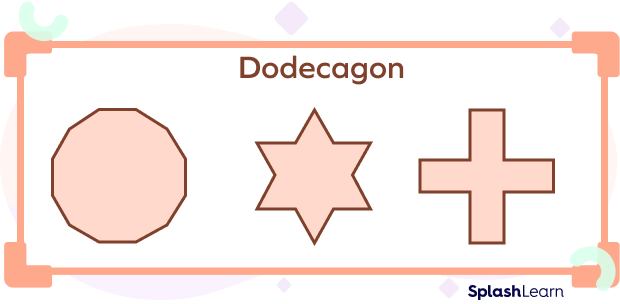
Based on the sides and angles, a dodecagon can be classified as a regular or irregular polygon and a convex or concave polygon. Let us now discuss the types of a dodecagon in detail.
Types of Dodecagons
On the basis of the side length and the angle measures, we can classify a dodecagon as regular and irregular dodecagons.
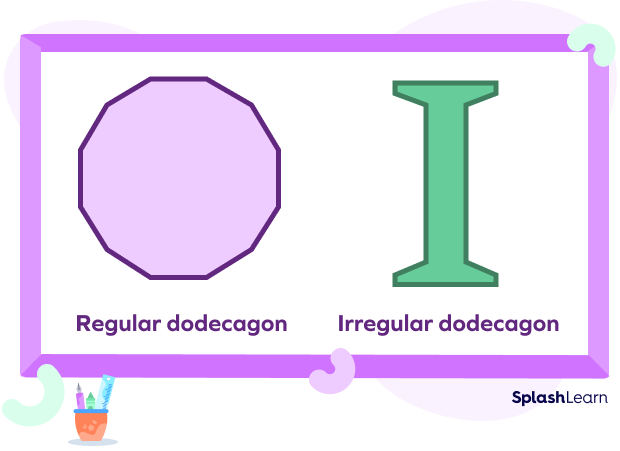
Regular and Irregular Dodecagons
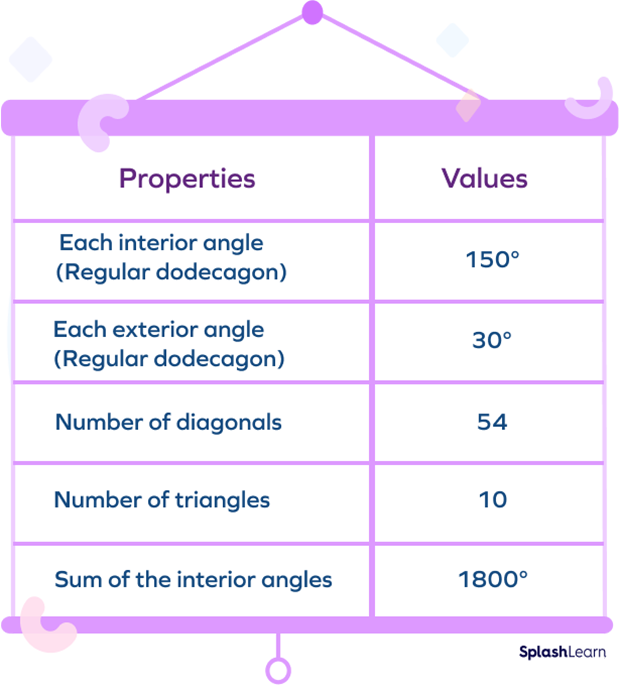
The 12 sided shape is regular when all the dodecagon sides and internal angles of the dodecagon are equal in measure. The 12 vertices of the polygon lie at an equal distance from the center. Each interior angle of this polygon measures 150 degrees. A regular dodecagon is one in which the vertices are spaced equally around a circle.
As the name suggests, in an irregular dodecagon, not all 12 sides of the polygon are identical in an irregular dodecagon. Due to the asymmetrical pattern of such dodecagons, even its 12 angles may vary from each other.
The following figure shows a regular and an irregular dodecagon.
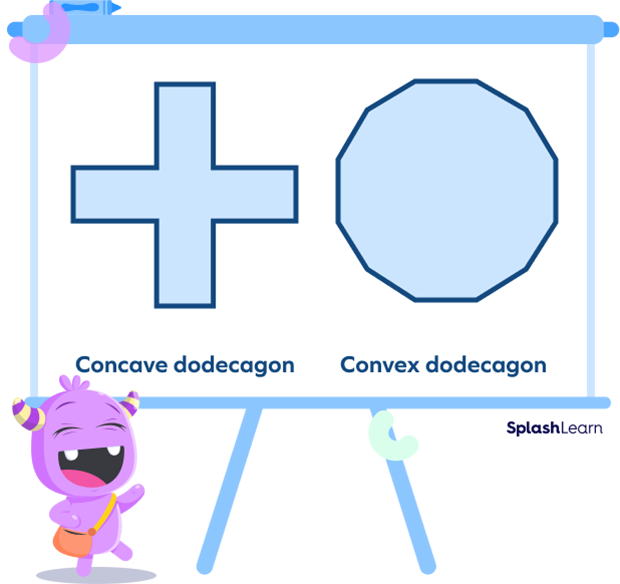
Concave and Convex Dodecagon
When any one of the interior angles of the polygon is greater than 180, we get a concave dodecagon. One or more of the vertices of such a dodecagon may point towards the center. A convex dodecagon, on the other hand, has all the interior angles less than $180^\circ$.
There is much to discuss regarding a dodecagon. In the following paragraphs, we will dive into a dodecagon’s properties, area, and perimeter.
Properties of a Dodecagon
A dodecagon is a 12-sided polygon. Basically, it is a polygon made up of 12 sides, 12 angles, and 12 vertices. Now let’s take a look at the properties of these polygons:
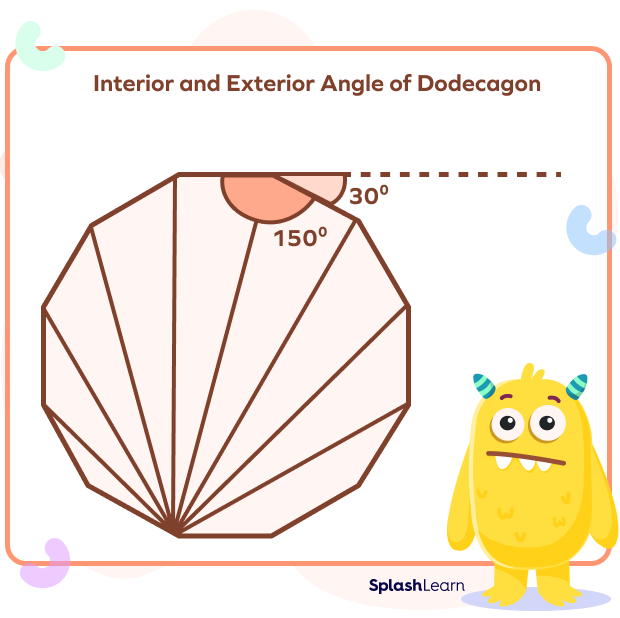
Interior and Exterior Angles
The sum of interior angles of a polygon can be calculated using the formula, $(n$$-$$2)360^\circ$ where n is the number of sides. Since the number of sides, i.e., $n =12$, in a dodecagon.
So, for dodecagon or for a 12 sided polygon, interior angles sum can be calculated using $n =12$.
The sum of interior angles of a dodecagon$=(12$$-$$2)\times360^\circ=10\times360^\circ=1800^\circ$
Thus, the sum of all the interior angles of a dodecagon is 1800.
In a regular 12-sided polygon, each angle is identical. So, each angle of a regular dodecagon is equal to $1800^\circ \div 12$ or $150^\circ$.
From the figure below, we can see that the exterior angle and the interior angle make a straight line. Each exterior angle of a regular 12-sided polygon is equal to $180^\circ$ $–$ $150^\circ$ or $30^\circ$. The sum of all the exterior angles of a 12-sided polygon is 360.
Diagonals of a Dodecagon
We can calculate the number of diagonals in any polygon using the formula:
$\frac{n (n-3)}{2}$, where n is the number of sides of the polygon. In this case, $\text{n} = 12$. So, the number of diagonals in the polygon is $\frac{12 (12 –3)}{2}$ or 54.
Triangles in a Dodecagon
We can calculate the triangles formed by diagonals from every vertex of a dodecagon. The formula for that is $(\text{n}$ $–$ $2)$.
Here, “n” is the number of sides of the polygon.
Facts
We can summarize the properties of dodecagon through a value table for better clarification.
Area of a Dodecagon
The area of a dodecagon means the total space covered by the boundary of the polygon. The mathematical formula to calculate area of a regular dodecagon is given as:
Dodecagon area formula: Area $= 3 \times ( 2 + \sqrt{3}) \times \text{s}^2$ ,
where s = length of its side
Perimeter of a Dodecagon
The perimeter represents the polygon’s boundary. It is the sum of all sides of the polygon. The perimeter of a regular dodecagon can be calculated by the formula
$\text{P} = \text{s} \times 12$, where “s” is the length of the side of a dodecagon.
Conclusion
A polygon is a two-dimensional closed geometric figure with a finite number of sides. A dodecagon is a 12-sided polygon. Knowledge of different types of polygons is essential for understanding various two-dimensional shapes in real life. SplashLearn is here to make this learning journey easier for you.
Solved Examples
1. What will be the area of a dodecagon with a side of 10 cm?
Solution:
Area of a dodecagon $= 3 \times (2 + \sqrt{3}) \times \text{s}^2$
Given that s $= 10$ cm,
Area $= 3 \times (2+ \sqrt{3}) \times 10^2 = 11.196 \times 100 = 1119.6$ $\text{cm}^2$
2. What will be the perimeter of a dodecagon which has a side of 5 cm?
Solution:
Formula for perimeter $= 12 \times$ side length $= 12 \times 5 = 60$ cm
3. Out of the two images given below, identify which one is a dodecagon.
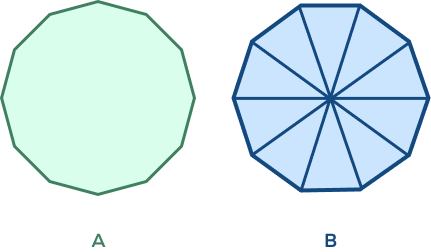
Solution:
A dodecagon is a polygon with 12 sides. Hence, image A is the right answer.
4. What will be the length of wire needed to fence a park in the shape of a dodecagon if the length of each side of the park is 100 m?
Solution:
We know that a $12 \times$ side gives the perimeter of a dodecagon.
Given that S $= 100$ m,
Perimeter $= 12 \times 100$,
The perimeter so obtained represents the park boundary that needs to be fenced.
5. What is the sum of all the exterior angles of a regular dodecagon?Solution: Each exterior angle of a regular 12-sided polygon is equal to $30^\circ$. So, the sum of all the 12 exterior angles of a 12-sided polygon is $30^\circ \times 12 = 360^\circ$
Practice Problems
Dodecagon
Each interior angle of a regular dodecagon is
Each interior angle of a regular dodecagon measures 150O, which is an obtuse angle.
Which of the following is a dodecagon?




The figure in option A is a 12-sided polygon.

If one of the interior angles of a 12-sided polygon is 190o, then which of the following is true?
When any one of the interior angles of the 12-sided polygon is greater than 180we get a concave dodecagon.
A community park needs the installation of lamps at every corner. If the park is in the shape of a dodecagon, how many lamps must be installed in the park?
We know that a dodecagon has 12 angles along each vertex. If the park authority wants to place a lamp at each vertex, they must order at least 12 lamps.
What will be the perimeter of a dodecagon if it has a side of 10 cm?
We know that a $12 $\times$ side gives the perimeter of a dodecagon.
Given that $\text{S} = 10$ cm,
Perimeter $= 12 \times 10 = 120$ cm
Frequently Asked Questions
Do the exterior and interior angles of a dodecagon form a straight line?
Yes, the two angles combined form a straight line, forming a linear pair of angles.
Which conditions must a dodecagon satisfy to qualify as a regular polygon?
A dodecagon must have 12 equal sides and 12 equal interior angles to qualify as a regular polygon.
What is a skew dodecagon?
A skew dodecagon has 12 vertices and edges that do not exist on the same plane. Such dodecagons generally do not have a defined interior space.
How can we split a dodecagon into several triangles?
We can do so by drawing diagonals from the vertices of a dodecagon. Usually, we can form up to 10 triangles within a dodecagon.
Is there any difference between a dodecagon and a dodecahedron?
A dodecagon is a 12-sided 2D polygon, but a dodecahedron is a three-dimensional polyhedron with 12 faces. Unlike a dodecagon, we can measure the volume of a dodecahedron.
















