What Is an Empty Set in Math?
An empty set is also called a null set or a void set. It is a set that has no elements. An empty set is denoted by $∅$ or $\left\{ \right\}$.
Consider an example. Let’s define set A as the set of perfect squares less than 0. However, we know that a perfect square is always a positive number. It means that the set A has no elements. Thus, it is an empty set. You can think of an empty set as an empty box or an empty container.
Recommended Games
Definition of Empty Set
An empty set can be defined as a set that does not contain any element. It is a set with cardinality 0.
Empty Set Examples:
- $P = \left\{y: \text{y is a leap year between 2008 and 2012}\right\}$
Between 2008 and 2012, there was no leap year.
Therefore, P is a null set.
- $Q = \left\{x : \text{x is a prime number and} x \lt 2\right\}$
We know that 2 is the only even prime number. However, we have an condition $x \lt 2$.
Thus, Q is an empty set.
Recommended Worksheets
Empty Set Symbol
The empty set is denoted by $∅$ or $\left\{ \right\}$.
How to Represent an Empty Set
As mentioned earlier, we can represent an empty set either with a special symbol ∅ or with the conventional curly brackets { } with no elements inside. Let’s understand the empty set notation with the help of examples.
- $A =$ Set of natural numbers less than $1 = \left\{ \right\}$.
- B is the set of real numbers satisfying $x^{2} + 1 = 0$.
The equation doesn’t have a real solution since -1 is not real.
Thus, $B = ∅$
- $∅ = \left\{x: \text{x is odd and x is a multiple of 2}\right\}$
Properties of Empty Set
Empty sets are incredibly useful for classifying unusual and odd objects. These empty sets make the calculations simpler. Due to some of their properties, these empty sets are significant.
Let’s examine these properties in order to better understand the idea of empty sets.
Cardinality
The cardinality of a set refers to the total number of elements present in the set. Empty set has no elements. The cardinality of the empty set is zero.
$|∅| = 0$
Empty set is a subset of every set.
For any set A, the empty set is a subset of A.
$∅\; ⊆$ A for any set A
It does not matter whether a set is finite or infinite. An empty set will always be the subset of the given set.
Subset of an Empty Set
The only subset of an empty set is the empty set itself.
If $A ⊆ \; ∅ A = ∅$
Cartesian Product of Empty Set
The Cartesian product of any set and the empty set is the empty set.
$A ∅ = ∅$
Power Set of Empty Set
An empty set or a null set does not contain any element. Thus, the power set of the empty set is the set containing only the empty set.
Union with Empty set
The union of A with the empty set is the set A itself. Since an empty set contains no elements at all, its union with any set A produces the same set A.
$A ⋃ ∅ = A$
Intersection with Empty Set
The intersection of A with the empty set is again the empty set. As the empty set contains no elements, there will be no common element between an empty and a non-empty set.
$A ⋂ ∅ = ∅$
Venn Diagram of Empty Set
A Venn diagram is a diagram used to visually represent sets, relationships between sets, and operations on sets.
A Venn diagram gives a clear idea about the different relationships between the given sets, such as union, intersection, or complement.

Example: Consider two sets.
$A = \left\{a, b, c\right\}$
$B = \left\{d, e, f\right\}$
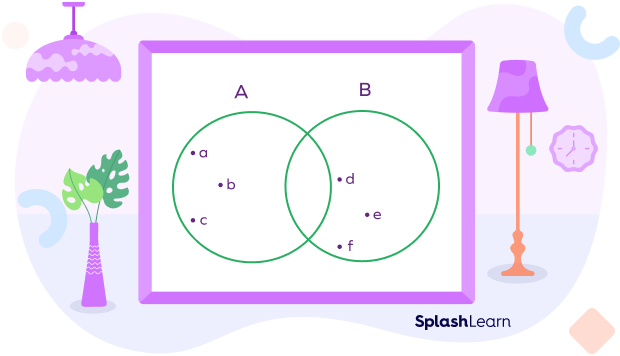
The Venn diagram shows that there are no common or intersecting elements between the two sets. Therefore we can infer that the intersection between the sets is empty.
Thus, $A ∩ B = ∅$.
Difference Between Zero Set and Empty Set
| Zero Set | Empty Set |
|---|---|
| A zero set is a zero set containing 0 as its only element. | The empty set or null set is a set with no elements. |
| Zero set is symbolically represented as $\left\{0\right\}$. | Empty set is symbolically represented as $∅$ or $\left\{ \right\}$. |
| Cardinality $= 1$ | Cardinality $= 0$ |
| Example: A set $A =$ Set of whole numbers less than 1 Thus, $A = \left\{0\right\}$ | Example:A set $B = \left\{x: \text{x is a prime number in between} 7 \lt x \lt 11\right\}$.Thus, $B = \left\{ \right\}$ or $∅$ |
Facts about Empty Set
- The empty set is also called the null set.
- The empty set is unique. It is the only set with no elements in it. There is only one empty set, regardless of the context or the definition of the universal set.
Conclusion
In this article, we have learned about the empty set, its properties and representation. Let’s solve some examples and practice problems to understand the concept better.
Solved Examples on Empty Set
1. Determine which of the following sets is empty.
a. $\left\{x : x + 4 = 7\right\}$
b. $\left\{x : x^{2} \;-\; x = 2 \right\}$
c. $\left\{x : 7 \lt x \lt 8, \text{x is a natural number.}\right\}$
Solution:
An empty set is a set having no elements.
Let’s find the elements of each set to determine which set is empty.
a. $\left\{x : x + 7 = 7 \right\}$
$x = 7 \;-\; 7$
$x = 0$
$\left\{x: x + 7 = 7\right\} = \left\{0\right\}$
This is a zero set. It is not an empty set.
b. $\left\{x : x^{2} \;-\; x=2\right\}$
$x (x \;-\; 1) = 2$
$x = 2$ or $x = \;-\; 1$
Thus, it is not an empty set.
c. $\left\{x: 7 \lt x \lt 8, \text{x is a whole number.}\right\}$
$\left\{x : 7 \lt x \lt 8, \text{x is a whole number}\right\}$ will be a null set because there is no whole number between numbers 7 and 8.
2. P is the intersection of the set of quadrilaterals with the set of triangles. Is the set P a null set?
Solution:
For a set to be null, the set must be empty, meaning there are no elements in it.
A quadrilateral is a polygon with 4 sides and 4 vertices.
A triangle is a polygon with 3 sides and 3 vertices.
Therefore, the set P is null.
3. Write whether the following statements are true or false.
a. An empty set is a subset of every set.
b. The set of odd natural numbers divisible by 2 is an empty set.
c. The set of odd prime numbers is an empty set.
Solution:
a. An empty set is a subset of every set.
True.
An empty set is a subset of every set.
b. The set of odd natural numbers divisible by 2 is an empty set.
True
Odd natural numbers are not divisible by 2. There is no natural number that satisfies the condition. Hence, it is an empty set.
c. The set of odd prime numbers is an empty set
False
The set of odd numbers $= \left\{3,\; 5,\; 7,\; 11,\; 13,\; 17,\; 19 …\right\}$
The given set has an infinite number of elements, so it is an infinite set.
Therefore, it is not an empty set.
Practice Problems on Empty Set
Empty Set: Definition, Properties, Notation, Symbol, Examples, FAQs
What is the cardinality of an empty set?
Null set or empty set is a set which does not contain any element. So, the number of elements in a null set is zero.
Which of the following is the representation of an empty set?
An empty set is a set that does not contain any element. It can be represented by $\left\{ \right\}$ or $∅$ symbol.
Which of the following is an empty set?
A factor of a number is always less than or equal to the number. So, there is no factor of 7, which is greater than 7. It is an empty set.
Find the solution to set $\left\{x : \text{x is a natural number and 2x + 1 = 2}\right\}$.
$2x + 1 = 2$
$2x = 1$
$x = 12$, which is not a natural number.
So, the set is empty and can be represented by$\left\{ \right\}$.
The empty set is also known as the
The empty set is a set that contains no elements. It is also known as null set, or void set.
Identify the null set symbol.
Null set $= \left\{ \right\} = ∅$
Frequently Asked Questions on Empty Set
Why is an empty set called a set?
We know that a set is a collection of well-defined objects. However, if we define a set using conditions that are not satisfied by any real number, the set will have no elements. If you subtract a set from itself, you will get A – A, which is a set with nothing in it. If the intersection of two sets A and B, since it is possible that A and B have no elements in common (for example, if A is the even integers and B is the odd integers). To define such sets, you need the empty set.
What is the power set of an empty set?
An empty set or a null set does not contain any element. The only subset of the empty set is the empty set itself. Thus, the power set of the empty set is the empty set.
Is an empty set a finite set?
Yes. Empty set has no elements in it. That implies its cardinal number is zero. Therefore, an empty set is considered a finite set.
Is $\left\{0\right\}$ a null set ?
No, there is one element inside the brackets. So, it is a singleton set, not a null set.
Is $\left\{∅\right\}$ an empty set?
No, $\left\{∅\right\}$ is not an empty set. An empty set is a set that does not contain any elements. The set $\left\{∅\right\}$ contains one element which is $∅$.
What is a non-empty set?
Any set with at least one element is a non-empty set.


































