Equivalent Ratios – Definition with Examples

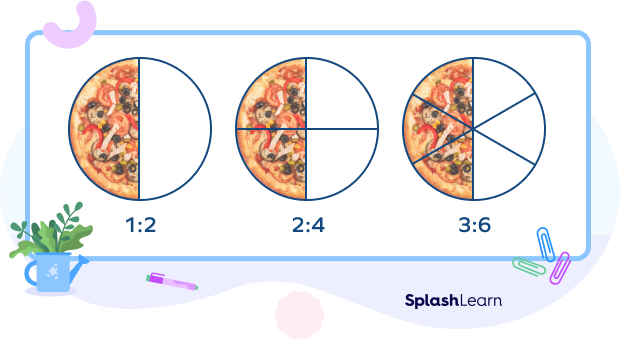
What Are Equivalent Ratios?

Two ratios that turn out to be the same in comparison are known as equivalent ratios. In order to check whether the given ratios are equivalent or not, we will have to simplify them or reduce them to their simplest form.

Example: Consider the ratios as 1:2, 2:4. 3:6. 

If you reduce 3:6 to its  simplest form, you get 1:2.

If you reduce 2:4 to its simplest form, you get 1:2.

Thus, these are equivalent ratios.

What Is a Ratio?

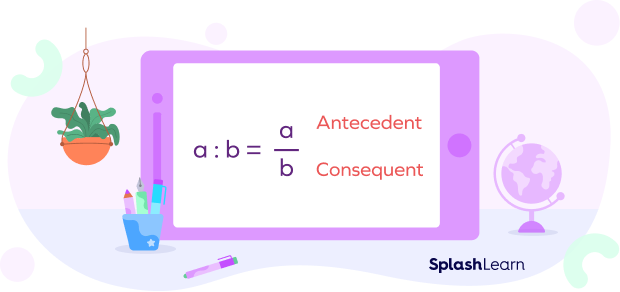
Ratio is defined as the quantitative relation or comparison between two different quantities of the same kind and same unit. In mathematics, the symbol “:” is used to express ratio, where a ratio is anything that compares two quantities of the same kind. 

Ratio of a to $b = a : b = \frac{a}{b}$ 

The first quantity of the ratio is called antecedent, whereas the second quantity of the ratio is called consequent. In the above example, 1 is the antecedent and 3 is the consequent. 

So, what are equivalent ratios? Let’s see an example.

Example: The ratio of the number of oranges to the number of apples in the fruit basket is 2:3 or $\frac{2}{3}$. Can you guess how many apples and oranges are there in the basket? 

Here’s the interesting part! Note that this does not mean that there are 2 oranges and 3 apples in the basket. It means that the number of oranges will be some multiple of 2 and the number of apples will be the multiple of 3 with respect to the same number. 

What are the possibilities then?

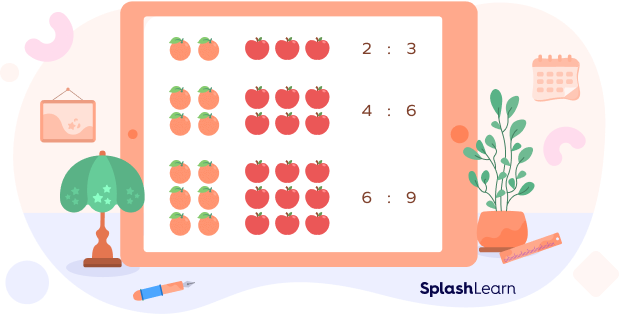
And so on, of course.

Here, the ratios 2:3, 4:6, 6:9 are equivalent ratios since they ultimately get reduced to the same value, 2:3.

Equivalent Ratios: Definition

Two ratios are said to be equivalent if they represent the same value when reduced to the simplest form.

Examples of equivalent ratios:

• 1:2 , 2:4, 3:6
• 3:7, 6:14, 9:21
• 4:3, 8:6, 20:15

What Is the Standard Form of Ratio?

The standard form of the ratio can be given as a:b, where a is the antecedent and b is the consequent. 

When a ratio is expressed in the form of a fraction it can be written as a/b or $\frac{a}{b}$. Here, a is the numerator and b is the denominator.

How to Identify Equivalent Ratios

We can use two methods. The first method is the cross multiplication method and the second method is the Highest Common Factor (HCF) method. Let us understand both of these methods with the help of examples.

Cross Multiplication Method

This method is convenient to use when the numbers involved are small. 

Check whether 12:18 and 10:15 are equivalent ratios or not using the cross multiplication method.

Step 1: Write the given ratios in the fractional form that is numerator by denominator form.

$12:18 = \frac{12}{18}$ and $10:15 = \frac{10}{15}$

Step 2: Cross multiply.

$12 \times 15 = 180$

$18 \times 10 = 180$

Step 3: If both products turn out to be equal, it would mean that the given ratios are equivalent ratios. 

Here, $12 \times 15 = 18 \times 10 = 180$.

Therefore, the given ratios (12:18 and 10:15) are equivalent ratios.

HCF Method

Let’s use the same example.

Step 1: We will find the HCF of the antecedent and consequent of both the given ratios. 

HCF $(12,18) = 6$

HCF $(10,15) = 5$

Step 2: Next, divide both the antecedent and consequent terms of both ratios by their respective HCF. So, we will get

$(12 \div 6) :(18 \div 6) = 2:3$

$(10 \div 5) :(15 \div 5)=2:3$

Step 3: If the reduced forms of both the given ratios are equal, it means that the given ratios are equivalent. 

Here, $12:18 = 10:15$.

How to Find Equivalent Ratios?

If one of the ratios can be expressed as a multiple of the other given ratio, then they are said to be equivalent ratios. Thus, creating equivalent ratios is simple.

As is the case for equivalent fractions, we can easily find an equivalent ratio by multiplying the given ratio (both antecedent and consequent) with the same natural number. 

Example: Find equivalent ratios of 1:4.

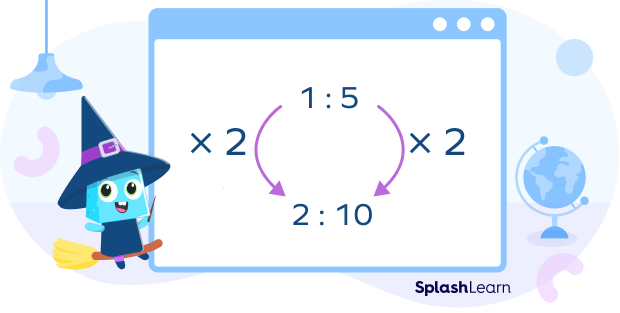
Equivalent ratios of 1:4 are 

2:8  … multiply 1:4 by 2

3:12 … multiply 1:4 by 3

4:16 … multiply 1:4 by 4

and so on.

Table of Equivalent: Ratios 

As we discussed earlier, we can easily find an equivalent ratio by multiplying the given ratio (both antecedent and consequent) with the same number. This number could be any natural number. We can find an infinite number of equivalent ratios for a given ratio. 

These equivalent ratios for a given ratio, when combined together and presented in a tabular format, gives us the required “Equivalent Ratios Table.” 

Let us make our own Equivalent Ratio Table when the given ratio is 5:3. All we have to do is to think of any natural number and then multiply both the terms of the given ratio with that number to obtain a unique equivalent ratio. 

$5:3 = (5 \times 2) :(3 \times 2) = 10:6$

$5:3 = (5 \times 3) : (3 \times 3) = 15:9$

$5:3 = (5 \times 4) : (3 \times 4) = 20:12$

$5:3 = (5 \times 5) : (3 \times 5) = 25:15$

Equivalent Ratio Table for the ratio 5:3 can thus be represented as,

Visual Representation of Equivalent Ratios

When we represent the equivalent ratios visually, the shaded area (and thus the unshaded area) is the same for each ratio.

Example:  1: 3

     2 : 6

     4 : 12

Fun Facts!

Conclusion

In this article, we learned about equivalent ratios definition and meaning in mathematics, what ratios are, what the standard form of ratio is, and how to find equivalent ratios. We also understood how to make the equivalent ratios table for a given ratio.

Solved Examples On Equivalent Ratios

1. Find one equivalent ratio of 3:22.

Solution: We will first write the given ratio in the form of a fraction.

$3 :22 \Rightarrow \frac{3}{22}$

Now we will multiply both the numerator and denominator by 2

$\frac{3 \times 2}{22 \times 2} = \frac{6}{44} = 6 : 44$

So, 8 :44 is an equivalent ratio of 3 :22.

2. Find any two equivalent ratios of 14 :21.

Solution: 

We will first write the given ratio in the form of a fraction.

$14:21 \Rightarrow \frac{14}{21}$

Now we will multiply both the numerator and denominator by 3, to get the first equivalent fraction.

$= \frac{14}{21}$

$= \frac{14 \times 3}{21 \times 3}$

$= \frac{42}{63}= \frac{14}{21}$

Again, multiply and divide 1421 by another natural number, such as 5, as given below:

$= \frac{14}{21}$

$= \frac{14 \times 5}{21 \times 5}$

$= \frac{70}{105} = \frac{14}{21}$

Hence, the two equivalent ratios of 14 :21 are 42 :63 and 70 :105.

3. Find any four equivalent ratios of 2:9. Present them with the help of the Equivalent Ratios Table.

Solution: 

$2:9 = (2 \times 2) : (9 \times 2) = 4:18$

$2:9 = (2 \times 3) : (9 \times 3) = 6:27$

$2:9 = (2 \times 4) : (9 \times 4) = 8:36$

$2:9 = (2 \times 5) : (9 \times 5) = 10:45$

Equivalent Ratio Table for ratio 2:9 can thus be represented as:

4. Are the ratios 18:10 and 63:35 equivalent?

Solution: 

Let’s use the HCF method.

HCF $(18,10) = 2$

HCF $(63:35) = 7$

$\frac{18 \div 2}{10 \div 2} = \frac{9}{5}$ and $\frac{63 \div 7}{35 \div 7} = \frac{9}{5}$

Both ratios in their reduced form are equal.

Thus, the ratios 18:10 and 63:35 are equivalent.

5. What will be the value of x if 2:5 is equivalent to 12:x?

Solution: 

It is given that $2 :5 = 12:x$. 

In fraction form, we write $\frac{2}{5} = \frac{12}{x}$

By cross multiplying, we get

$2x = 12 \times 5$

$2x = 60$

$x = 30$

Practice Problems On Equivalent Ratios

Frequently Asked Questions On Equivalent Ratios