Finding Slope of Line from Two Points: Formula, Example

What Is Finding Slope from Two Points?

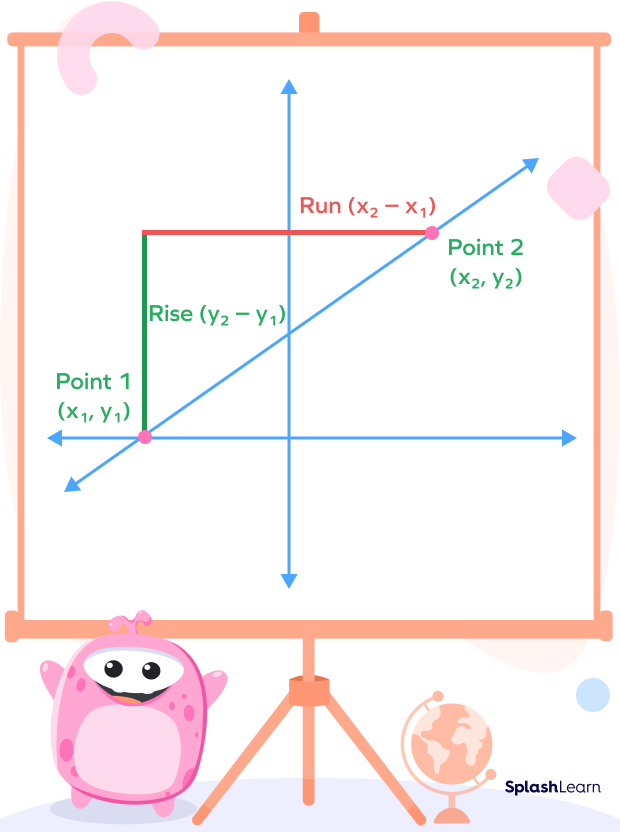
Finding slope from two points refers to finding the slope of a line when coordinates of two points on the line are given. The slope of a line is the measurement of the change in vertical distance over the change in the horizontal distance (rise-over-run ratio). Slope tells us how steep a straight line is.

The slope can be calculated by applying different formulas based on the given information about the line. When coordinates of two points on the line are given, then we use the formula for finding the slope from two points. Let us discuss its formula.

Finding Slope from Two Points Formula

As we discussed, the slope is defined by the rise-over-run formula. 

Slope $= m = \frac{\Delta y}{\Delta x} = \frac{Change\; in\; y}{Change\; in\; x}$

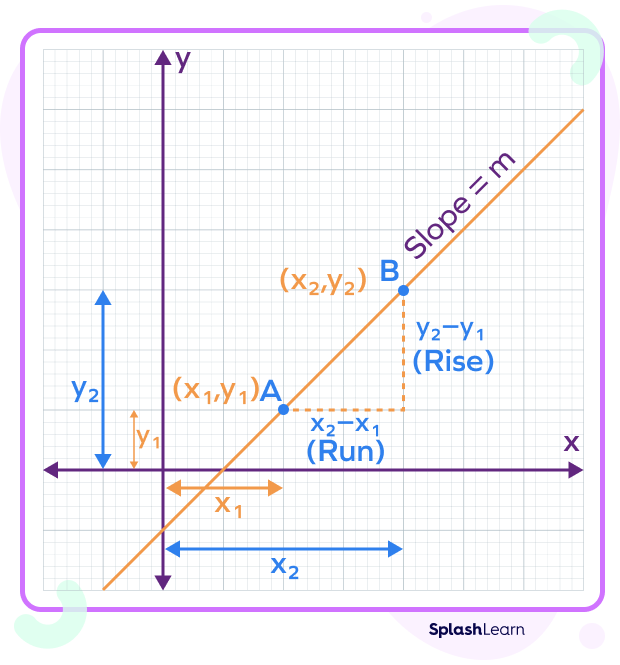
If a line passes through two points A and B whose coordinates are $(x_1,\; y_1)$ and $(x_2,\; y_2)$, then the slope formula is given by

slope $= m = \frac{Rise}{Run} = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1}$

Here,

$m =$ slope of the line

$x_1 =$ the x-coordinate of the point A

$y_1 =$ the y-coordinate of the point A

$x_2 =$ the x-coordinate of the point B

$y_2 =$ the x-coordinate of the point B

Derivation of the Formula for Finding Slope from Two Points

Let $\theta$ be the angle formed by the line with the positive direction of the x-axis. 

Let $A\;(x_1,\; y_1)$ and $B\;(x_2,\; y_2)$ be two points on the line. Draw a horizontal and vertical line through the points A and B that intersect at C.

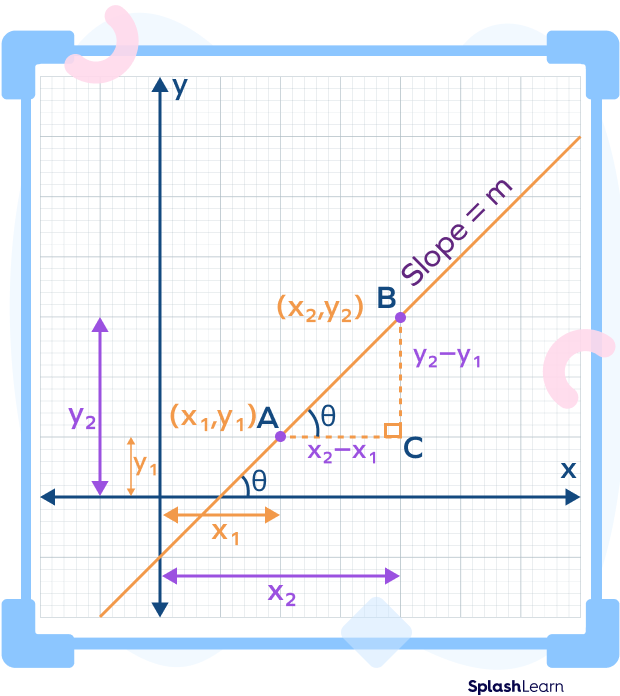
As we know if a line makes angle θ with the positive x-axis in the anticlockwise direction, then its slope is given by 

Slope $= m = tan\; \theta$ …(i)

Also, from the above figure, $\angle A = \theta$ (corresponding angle)

Now, in triangle ABC,

$tan\theta = \frac{Opposite\;side}{Adjacent\;side} = \frac{BC}{AC}$

$\Rightarrow tan\theta = \frac{y_2-y_1}{x_2-x_1}$ …(ii)

From equation (i) and (ii), we get the formula/equation for finding slope with two points $(x_1,\; y_1)$ and $(x_2,\; y_2)$ on the line as

$m = \frac{y_2-y_1}{x_2-x_1}$

How to Find Slope from Two Points

Let’s look at the steps for finding slope from two points.

• Use $(x_1,\; y_1)$ to identify the first point.
• Use $(x_2,\; y_2)$ to identify the second point.
• Find $(y_2- y_1)$, the difference between y-coordinates, and $(x_2- x_1)$, the difference between the x-coordinates. 
• To find the slope (m), divide the difference between y-coordinates by the difference between x-coordinates. 

$m = \frac{y_2- y_1}{x_2- x_1}$.

Note: While finding the slope, we can interchange points without affecting the result. The order of the points does not matter.

 $m = \frac{y_1- y_2}{x_1- x_2} = \frac{y_2- y_1}{x_2- x_1}$

Facts about Finding Slope from Two Points

• The slope is also known as “gradient.”
• The slope of a vertical line is undefined.
• The slope of any horizontal line is zero.
• For the line having a positive slope, the rise-over-run ratio is always positive.
• For the line having a negative slope, the rise-over-run ratio is always negative.
• The slope of parallel lines is equal. $(m_1 = m_2)$
• The slopes of two perpendicular lines are negative reciprocals of each other. $(m_1 = \frac{-1}{m_2})$
• If the three points A, B, and C are collinear, then 

slope of $AB =$ slope of $BC =$ slope of AC

Conclusion

In this article, we have learned about finding slopes with two points, its formula, derivation, steps of finding slopes from two points. Let’s solve a few examples for better understanding.

Solved Examples on Finding Slope From Two Points

1. Calculate the slope of a line passing through the points $P(\;–1,\; 3)$ and $Q(2,\; 15)$.

Solution:

The line passes through the points $P(\;–1,\; 3)$ and $Q(2,\; 15)$.

$(x_1,\; y_1) = (\;–1,\; 3)$

$(x_2,\; y_2) = (2,\; 15)$

Slope of line $PQ = m = \frac{y_2-y_1}{x_2-x_1} = \frac{15 – 3}{2 \;-(\;-1)} = \frac{12}{3} = 4$

Hence, the slope of the line PQ is 4.

2. What is the slope of a line if rise $= 100$ inches and run $= 25$ feet?

Solution:

Rise $= 100$ inches

Run $= 25$ feet $= 25\times12 = 300$ inches (1 foot $= 12$ inches)

Hence, slope $= \frac{Rise}{Run} = \frac{100}{300} = \frac{1}{3}$

3. If the slope of the line joining two points $(\;–1,\; 2k)$ and $(\;–2,\; k+2)$ is $–2$, then find the value of k.

Solution:

Slope of the line $= –2$

The line passes through the points $(\;–1,\; 2k)$ and $(–\;2,\; k+2)$.

$(x_1,\; y_2) = (\;–1,\; 2k)$

$(x_2,\; y_2) = (\;–2,\; k + 2)$

Slope $= \frac{y_2-y_1}{x_2-x_1}$

$\Rightarrow -2 = \frac{k + 2 – 2k}{\;-2\;-(\;-1)}= \frac{-\;k+2}{-\;1}$

$\Rightarrow -k + 2 = 2$

$\Rightarrow k = 0$

Hence, the value of k is 0.

4. If the three points A(2, 3), B(4, 0) and C(6, k) are collinear, find k.

Solution:

Given points are $A\;(2,\; 3),\; B\;(4,\; 0)$ and $C\;(6,\; k)$

For collinearity of three points A, B, and C, we write 

Slope of AB $=$ Slope of BC

$\Rightarrow \frac{0-3}{4-2} = \frac{k-0}{6-4}$

$\Rightarrow \\frac{-3}{2} = \frac{k}{2}$

$\Rightarrow k = -3$

Hence, three points $A\;(2,\; 3),\; B\;(4,\; 0)$ and $C\;(6,\; k)$ are collinear for $k=-3$.

5. Derive the condition for zero slopes from two points $(x_1,\; y_1)$ and $(x_2,\; y_2)$.

Solution:

Given points are $(x_1,\; y_1)$ and $(x_2,\; y_2)$.

The slope of line $= \frac{y_2-y_1}{x_2-x_1} = 0$

For zero slope,

$\frac{y_2-y_1}{x_2-x_1} = 0$

$\Rightarrow y_2\;-\;y_1 = 0$

$\Rightarrow y_2 = y_1$

Hence, the condition for zero slopes is $y_2 = y_1$.

If y-coordinates are the same, we get a horizontal line whose slope is always 0.

Practice Problems on Finding Slope from Two Points

Frequently Asked Questions on Finding Slope from Two Points