Adding Mixed Numbers

Adding Mixed Numbers

A mixed number is a type of fraction that has two parts: a whole number and a proper fraction. It is also known as a mixed fraction.  

Normally, a mixed number represents a number between any two whole numbers. We often come across examples of mixed numbers in our daily life.

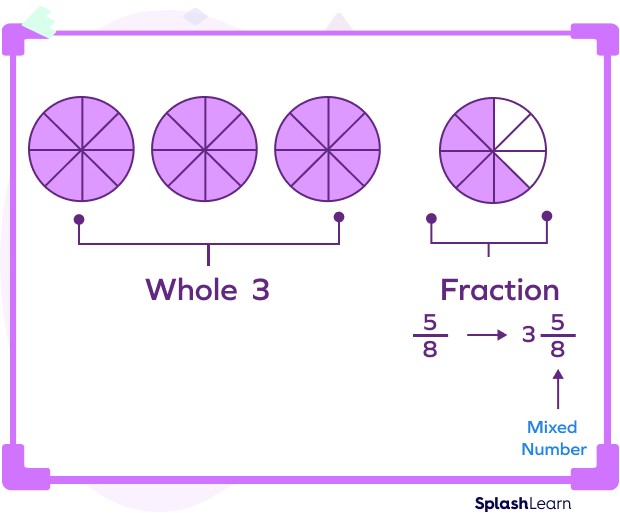
Let us consider the fraction $3\frac{5}{8}$. It consists of a whole number 3 and a fractional part $\frac{5}{8}$. Since the fractional part $\frac{5}{8}$ has the numerator 5, which is less than the denominator 8, it represents a proper fraction.  

So, the fraction $3\frac{5}{8}$ represents a mixed number.  

How to Add Mixed Numbers?

For adding mixed numbers (or adding mixed fractions), we take the whole numbers and fractions and add them separately. We then put them together.   

Let us understand this with the help of an example.

Example: Find the sum of  $2\frac{1}{8}$ and $3\frac{3}{8}$.

Here, we have to add two mixed numbers.

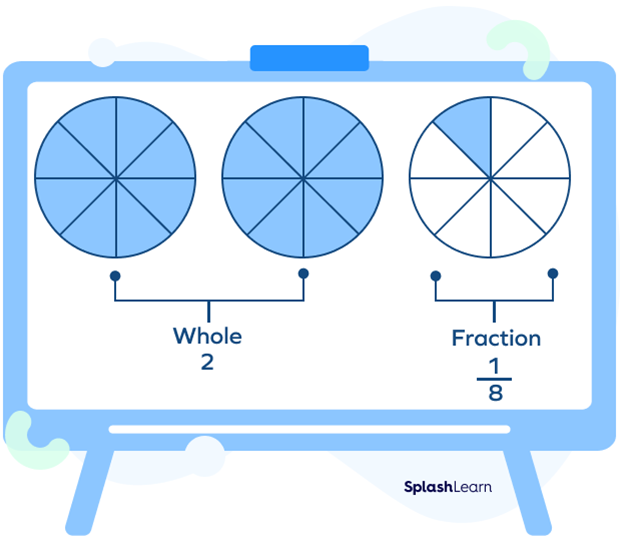
The first number is $2\frac{1}{8}$. 

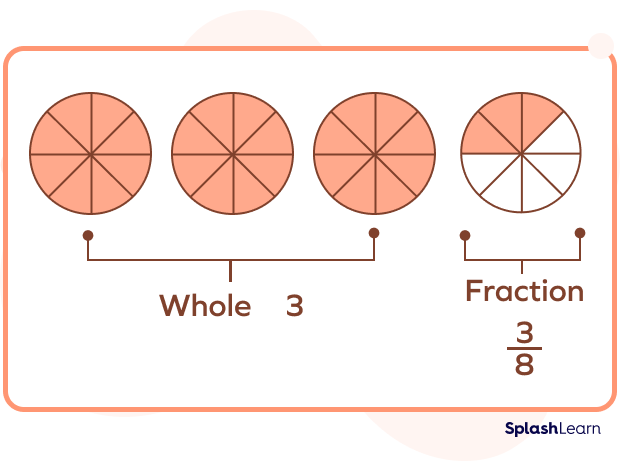
The second number is $3\frac{3}{8}$.

Visually, the two fractions, when added, would look like this:

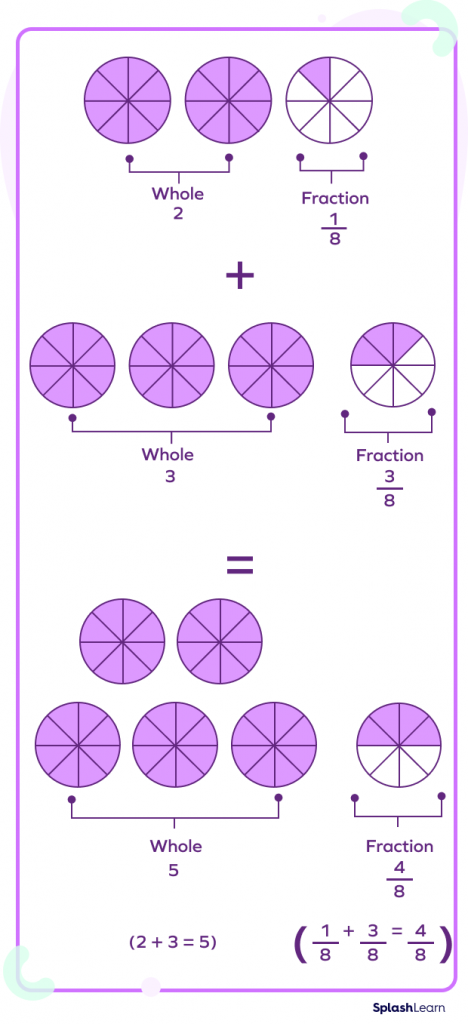
Now, let’s see how we can add the numbers  $2\frac{1}{8}$ and $3\frac{3}{8}$ without the help of models.

We first add the whole parts of both the mixed numbers.

Here, the wholes are 2 and 3. Let’s add them first.

2 + 3 = 5

And now we will add the fractional parts.

The fraction parts are $\frac{1}{8}$ and $\frac{3}{8}$. Let’s add them the way we would add two like fractions, add numerator to numerator and denominator to denominator.

$\frac{1}{8} + {3}{8}$

$= \frac{1 + 3}{8}$

$= \frac{4}{8}$

Now that we have the separate sums of the wholes and the fractions, we will put them together.

So, we get $2\frac{1}{8} +3\frac{3}{8} =5\frac{4}{8}$  

Now, let us see an example of adding two mixed numbers where our resultant fraction is not a proper fraction.

For instance, let’s say there are $2\frac{4}{5}$ lb of apples in one basket and $3\frac{3}{5}$ lb in another basket. How many apples are there altogether in both the baskets? 

Here, to find the number of apples in both the baskets, we add the mixed numbers $2\frac{4}{5}$ and  $3\frac{3}{5}$. The denominators of both the fractional parts are the same. So, to add mixed numbers with like denominators, we add the whole parts together and the fractional parts together and then combine the sum of the two as shown below:

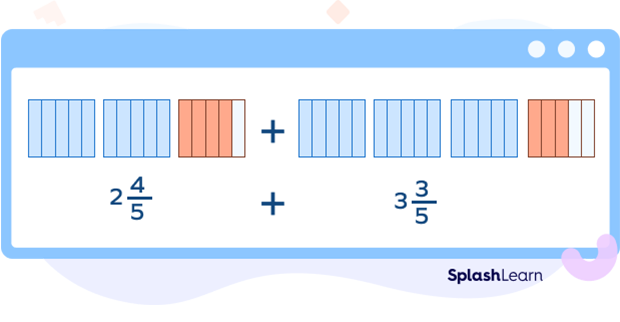
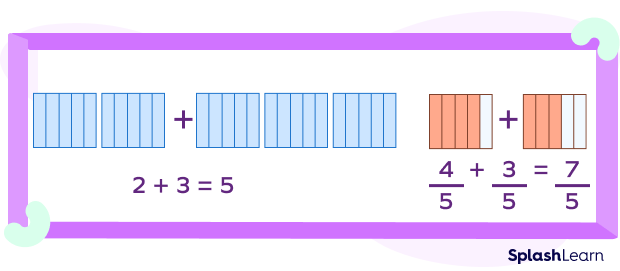
Add the whole part with the whole part and the fractional part with the fractional part.

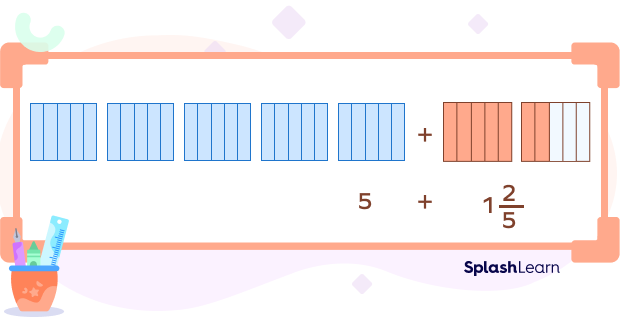
If the sum of the fractional parts is an improper number, convert it to another mixed number.

Combine the sum of the wholes and fractions.

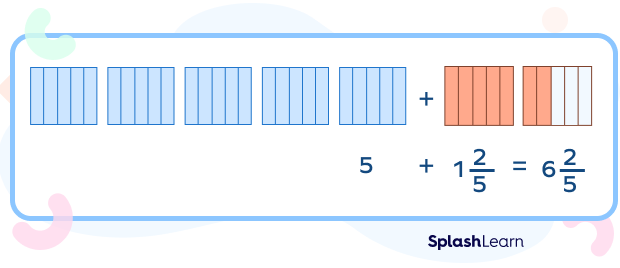
Therefore, there is $6\frac{2}{5}$ lb of apples. 

Mathematically, this addition would look like this:

$2\frac{4}{5} +3\frac{3}{5} = 2 + 3 + \frac{4}{5} + \frac{3}{5}$

$= 5 + \frac{7}{5}$

$= 5 + 1\frac{2}{5}$

$= 6\frac{2}{5}$

Adding Mixed Numbers with Unlike Denominators

Now, let us look at an example to understand the addition of mixed numbers with unlike denominators.

Let’s say Susan has $1\frac{4}{7}$ ounces of orange juice, and Keith has  $2\frac{2}{5}$ ounces of orange juice. How much orange juice do they have altogether? 

Here, we will find the answer by adding mixed numbers $1\frac{4}{7}$ and  $\frac2{2}{5}$. Here, the denominators of both the fractional parts are different. 

To add mixed numbers with unlike denominators, the best way is to convert both the mixed numbers into improper fractions and then add them just the way we would add two unlike fractions.

Step 1: Convert the mixed numbers into improper fractions.

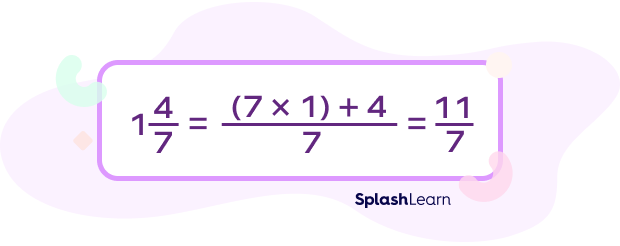
and 

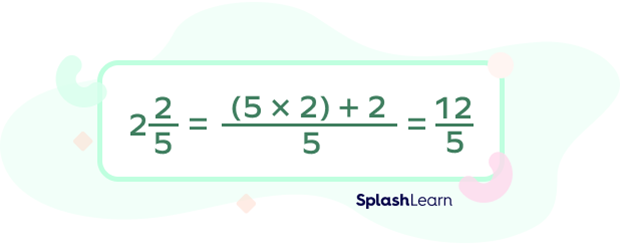
Step 2: Add the unlike improper fractions.

Here, we need to add the unlike fractions $\frac{11}{7}$ and $\frac{12}{5}$

Multiples of 7: 14, 21, 28, 35, 42

Multiples of 5: 5, 10, 15, 20, 25, 20, 35. 

So, the LCM is 35.

Now, we convert the fractions into equivalent fractions with denominator as the LCM.

$\frac{11}{7} = \frac{11}{7}  × \frac{5}{5} = \frac{55}{35}$

$\frac{12}{5} = \frac{12}{5}  × \frac{7}{7} = \frac{84}{35}$

So,

$\frac{11}{7} + {12}{5} = \frac{55}{35} + 8435 = 55 + 8435 = 13935

Step 3: Convert the final result into an improper fraction.

$\frac{139}{35}=3\frac{34}{35}$

Solved Examples

Example 1: David ate 3 ½ pizza slices while Jai ate 5 ⅔ pizza slices. How many pizza slices did they eat in total?

Solution: The problem comes down to adding mixed numbers. We will add 3 ½ + 5 ⅔.

Example 2: Ron walked $3\frac{2}{7}$ miles during a forest trip while his friend walked for $2\frac{4}{7}$ miles. How much distance did they both cover during the trip?

Solution: We will find the answer by adding mixed numbers, $3\frac{2}{7}$ and  $2\frac{4}{7}$. 

Here, the wholes are 2 and 3. Let’s add them first.

$2 + 3 = 5$

And now we will add the fractional parts.

The fraction parts are $\frac{2}{7}$ and $\frac{4}{7}$.

$\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}$

So, we get $3\frac{2}{7} +  2\frac{4}{7}=5\frac{6}{7}$

So, Ron and his friend covered $5\frac{6}{7}$ miles during their trip.

Practice Problems

Frequently Asked Questions