What Do We Mean by Dividing Fractions?
By dividing fractions we mean the division involves at least one fraction. For example,
- $\frac{3}{4} \div \frac{1}{2}$
- $7 \div \frac{1}{2}$
- $\frac{3}{4} \div 6$
The quotient of such multiplication could be a fraction or a whole number.
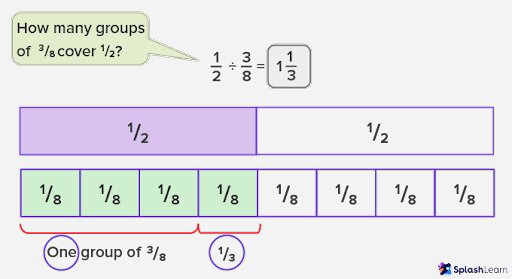
Let’s consider some examples to see what it means to divide fractions through visual models.
- Whole Number ÷ Fraction
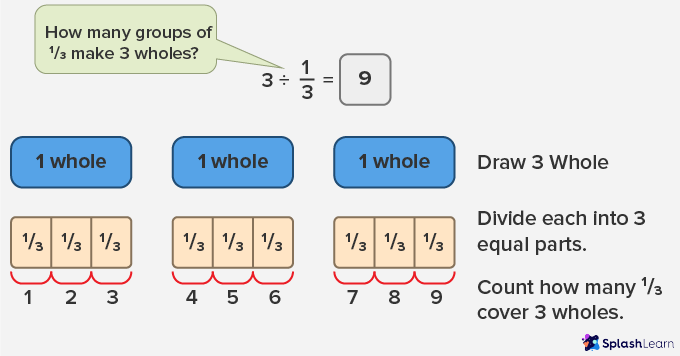
- Fraction ÷ Whole
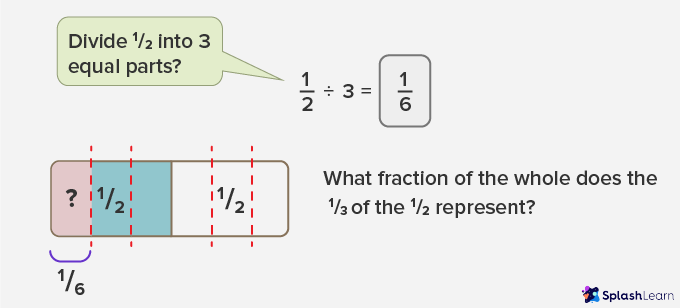
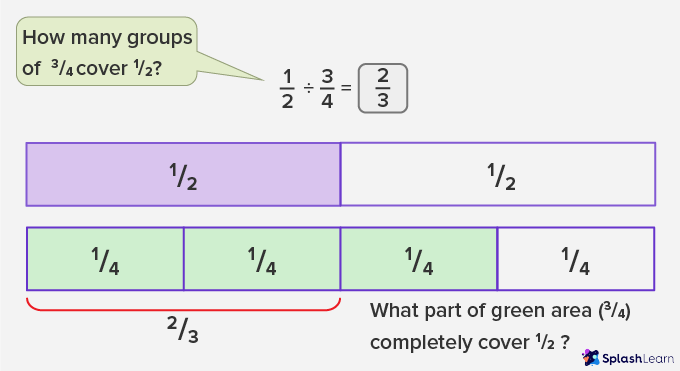
- Fraction ÷ Fraction
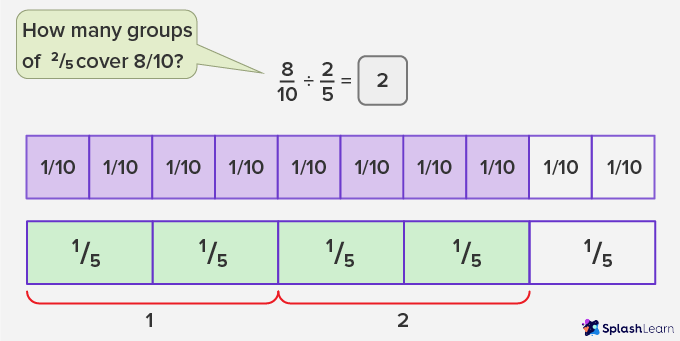
Visualising Fraction Division that Involves Remainder
Example 1:
Example 2:
Recommended Games
Steps to Divide Fractions
- Fraction by Fraction
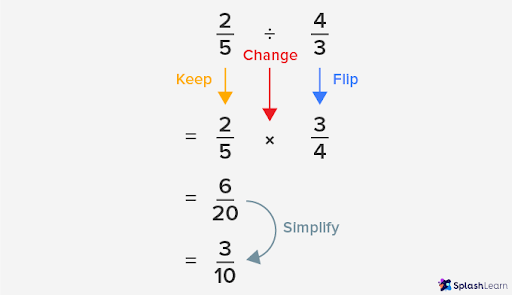
To divide a fraction by another fraction, multiply the dividend fraction by the reciprocal of the divisor fraction. The reciprocal of a fraction can be found by interchanging its numerator and denominator. For example, $\frac{3}{4}$ is reciprocal of $\frac{4}{3}$ and vice-versa.
There is a quick way to remember the steps to divide fractions: Keep >> Change >> Flip.
Follow these steps to divide a fraction by fraction (either proper or improper):
STEP 1:
Keep the dividend the same.
Change the division sign to multiply
Flip the divisor by writing its reciprocal.
STEP 2: Multiply the fractions
STEP 3: Simplify the result, if needed.
Quick Tip: In case the dividend and/or divisor are mixed numbers, we first convert them into improper fractions and then follow the steps mentioned above.
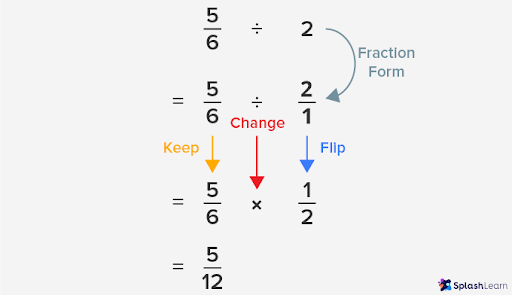
- Fraction by Whole Number
Recall that the reciprocal of a whole number ‘a’ is the unit fraction $\frac{1}{a}$ because we can write a whole in fraction form with denominator equal to 1, that is, $\frac{a}{1}$.
Let’s understand how to divide when divisor is a whole number through an example:
Why do we flip the divisor after changing the division sign?
When we divide one number by another, let’s say, a is the dividend and b is the divisor, then we can write it as $\frac{a}{b}$. Also, we can write $\frac{a}{b}$ as the product of a and $\frac{1}{b}$. That is,
$a \div b = \frac{a}{b} = a \times \frac{1}{b}$
We can also understand it like this:
Division is the inverse operation of multiplication. So, dividing by a number is the same as multiplying by its reciprocal.
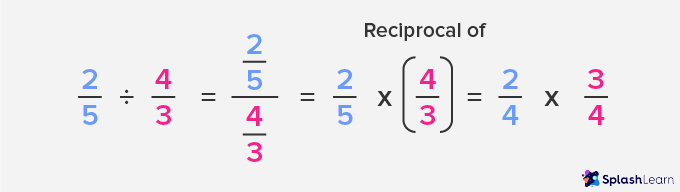
Recommended Worksheets
Properties of Dividing Fractions
The properties of division with whole numbers hold true for fractions as well. Let’s check!
- Property 1: When a fraction is divided by 1, the quotient is the fraction itself. $\frac{3}{4} \div 1 = \frac{3}{4}$
- Property 2: When zero is divided by a non-zero fraction, then the quotient is always 0.
$0 \div \frac{3}{4} = 0$ - Property 3: When a non-zero fraction is divided by itself, then the quotient is 1.
$\frac{3}{4} \div \frac{3}{4} = 1$ - Property 4: Division by 0 is not possible and the result is not defined.
$\frac{3}{4}\div 0 =$ Not Defined
Solved Examples
Example 1: Divide: $\frac{1}{5} \div \frac{1}{10}$.
Solution:
Keep $\frac{1}{5}$ as it is; change ÷ to × and flip $\frac{1}{10}$ and write it as $\frac{10}{1}$.
$\frac{1}{5} \div \frac{1}{10} = \frac{1}{5} \times \frac{10}{1} = \frac{10}{5} = \frac{2}{1} = 2$
Example 2: Divide: $1 \frac{2}{3} \div \frac{5}{7}$
Solution: Change 123 to improper fraction and then follow the steps to divide fractions.
$1\frac{2}{3} \div \frac{5}{7} = \frac{5}{3} \div \frac{5}{7} = \frac{5}{3} \times \frac{7}{5} = \frac{7}{3} = 2\frac{1}{3}$
Example 3: Max is painting toy cars. He has $2\frac{1}{4}$ L of paint. If each car requires $\frac{7}{3}$ L of paint, how many cars can Max paint?
Solution:
Quantity of paint with Max $= 2\frac{1}{4}$ L $= \frac{9}{4}$ L
Quantity of paint required to paint 1 car $= \frac{3}{8}$ L
Numbers of toy cars that Max can paint $= \frac{9}{4} \div \frac{3}{8}$
$= \frac{9}{4} \times \frac{8}{3}$
$= \frac{72}{12} = 6$
So, Max can paint 6 toys with $2\frac{1}{4}$ L of paint.
Example 4: Melvin sang a medley of songs for 10 minutes. If one song was $2\frac{1}{2}$ minutes long, how many songs did Melvin sing?
Solution:
Duration for which Melvin sang $= 10$ minutes
Length of one song $= 2\frac{1}{2}$ minutes
Numbers of songs that Melvin sing $= 10 \div 2\frac{1}{2}$
$= 10 \div \frac{5}{2}$
$= 10 \times \frac{2}{5}$
$= \frac{20}{5} = 4$
So, Melvin sang 4 songs in 10 minutes.
Practice Problems
Dividing Fractions
Divide: $\frac{7}{8} \div \frac{3}{9}$
$\frac{7}{8}\div\frac{3}{9} = \frac{7}{8}\times\frac{9}{3} = \frac{63}{24} = \frac{21}{8}$
Divide: $\frac{4}{8}\div 9$
$\frac{4}{8}\div 9 = \frac{4}{8}\times\frac{1}{9} = \frac{4}{72} = \frac{1}{18}$
Divide: $1\frac{1}{7}\div \frac{3}{5}$
$1\frac{1}{7}\div\frac{3}{5} = \frac{8}{7}\div\frac{3}{5} = \frac{8}{7}\times\frac{5}{3} = \frac{40}{21}$
Divide: $\frac{3}{7}\div\frac{3}{7}$
When a fraction is divided by itself, the answer is 1.
Frequently Asked Questions
What does division of fractions mean?
The division of fractions means dividing a fraction into further equal parts. For example, If you have three-fourth of a pizza left and you divided each slice into 2 parts you would get a total of six slices but this would represent six-eighths of the total pizza.
What is the method of dividing fractions?
The first step for dividing fractions is to reciprocate the second fraction, that is, exchange its numerator and denominator. Next, multiply the first fraction with this reciprocal using standard method of fracton multiplication and convert the answer into simplest form.
How does one divide a fraction by a whole number?
To divide a fraction by a whole number, convert the whole number into a fraction with denominator 1 and then follow the standard steps of dividing fractions i.e., Flip the second fraction and multiply this with the first fraction.
How do you divide fractions by mixed number?
To divide a fraction by a mixed number (or vice versa), convert the mixed number into an improper fraction and then follow the standard steps of dividing fractions.




































