What Are Fractions?
Fractions represent the parts of a whole or collection of objects. When the whole or collection is divided into equal parts, each part makes up a fraction. For example, if a pizza is divided into six equal slices, each slice is said to be 1/6 of the pizza. It means one in six equal parts. It can also be read as ‘one-sixth’, or ‘1 by 6’.

If we select two slices of the pizza, it will be 2/6 of the pizza. Similarly, if we select three slices of this pizza, it would be 3/6 of the pizza.
The number on the top of the line is called the numerator. It tells us how many equal parts of the whole are taken. The number below the line is called the denominator. It shows the total number of equal parts the whole is divided into.
Majorly, there are three types of fractions.
Proper fractions: When the numerator of a fraction is less than its denominator, it is a proper fraction. For example, ⅙, ⅜, ⅘ are proper fractions.
Improper fractions: When the numerator of a fraction is more than or equal to its denominator, it is called an improper fraction. For example, 4/3, 8/5, 6/4 are improper fractions.
Mixed fractions: Mixed fractions consist of a whole number along with a proper fraction. For example, $3\frac{4}{7}$, $4\frac{2}{5}$ are mixed fractions.
Recommended Games
What is a Fraction Greater than 1?
In a fraction, the denominator represents the total number of equal parts the whole is divided. We can say that the denominator represents the whole and the numerator represents the selected part of the whole. If the numerator of the fraction is greater than the denominator, then it is a fraction greater than one whole. For example,
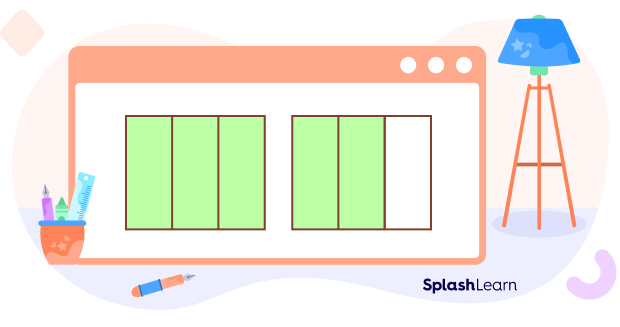
If each rectangle is equally divided into 3 parts, 5 parts is more than the one whole (or 3 parts). Therefore, 5/3 is greater than 1.
When the numerator of a fraction is greater than its denominator, the value of the fraction is greater than 1. These fractions are also called improper fractions.
Recommended Worksheets
How Are Fractions Greater than 1 Converted into Mixed Fractions?
Mixed numbers are considered to be the simple form of improper fractions. That is why it is essential to learn the conversion between them.
For converting a fraction greater than 1 or an improper fraction to a mixed number, we have to follow the steps given below:
- Step 1: Divide the numerator by the denominator and obtain the quotient and remainder.
- Step 2: Arrange the values of the quotient, remainder, and divisor in the following manner to obtain the mixed fraction.
$Quotient\frac{Remainder}{Divisor}$
The denominator of both improper fraction and its mixed fraction form is always the same.
For instance, the mixed fraction form of $\frac{7}{4}$ is 1 ¾.
Fractions Greater than 1 on a Number Line
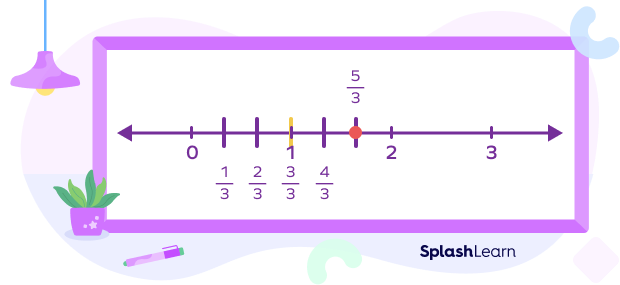
To plot fractions greater than 1 on a number line, we need to determine between which two whole numbers the fraction lies. We can do this by converting it into a mixed number.
For example, 5/3 = 1 ⅔
Looking at the number, we know our fraction is bigger than 1. So, it will be between 1 and 2. Divide the interval between 1 and 2 into 3 equal parts.
This will be the mixed number 1 ⅔ or the fraction 5/3.
Convert Fractions Greater than 1 to Decimals
To convert fractions greater than 1 into decimals, divide the numerator by the denominator. For example, $\frac{17}{10}$ = 1.7
To convert a mixed number to a decimal, divide the numerator by the denominator of the fraction part and add the whole part.
For example, $1\frac{3}{10}$ = 1 + 0.3 = 1.3
Solved Examples
Example 1: Is $\frac{9}{7}$ greater than 1?
Solution: In a fractions greater than 1, the numerator is greater than the numerator. Therefore, $\frac{9}{7}$ is the fraction of greater than 1.
Example 2: Convert $\frac{15}{7}$ into mixed fractions.
Solution: On dividing 15 by 7, we will get 2 as a quotient and 1 as a reminder.
We can write the mixed fraction $Quotient \frac{Remainder}{Divisor}$ or $2\frac{1}{7}$.
Example 3: Is $\frac{14}{5}$ − $\frac{12}{5}$ greater than 1?
Solution: $\frac{14}{5}$ − $\frac{12}{5}$ = $\frac{2}{5}$
Since the numerator is less than the denominator, its value is less than one.
Practice Problems
Fraction Greater Than 1 - Definition with Examples
Which of the following will be the answer if we convert $\frac{14}{3}$ into a mixed fraction?
When we divide 14 by 3, we will get 4 as the quotient and 2 as the remainder.
State whether the below statements are true or false.
1. Fractions greater than one are called proper fractions.
2. Improper fractions can be converted into mixed fractions.
Fractions greater than 1 are called improper fractions.
Improper fractions can be converted into mixed fractions.
The fraction 9/4 on a number line will be between which two numbers?
9/4 is equal to 2 ¼. On the number line, this fraction lies between 2 and 3.
Frequently Asked Questions
What is the difference between fractions greater than 1 and fractions less than 1?
If the numerator of the fraction is greater than its denominator, then the fraction is greater than 1. These are also called improper fractions. These fractions lie on the right side of 1 on the number line.
If the numerator of the fraction is less than its denominator, then the fraction is less than 1. These are also called proper fractions. These fractions lie between 0 and 1 on the number line.
What is the significance of comparing fractions with one whole?
As fractions are part of a whole, comparing fractions with a whole helps us determine the different types of fractions. Fractions less than 1 are proper fractions. Fractions greater than 1 can be written as improper fractions or mixed numbers.
Can a mixed fraction be less than 1?
No, a mixed fraction combines a whole number and a proper fraction. Hence, it is always greater than 1.




































