What Are Fractions?
Fractions represent the parts of a whole or collection of objects. When the whole or collection is divided into equal parts, each part makes up a fraction. For example, if a pizza is divided into eight equal slices, each slice is said to be $\frac{1}{8}$ of the pizza. It means one in eight equal parts. It can also be read as ‘one-eighth’, or ‘1 by 8’.
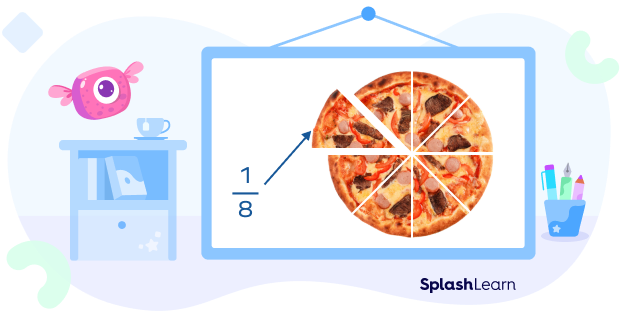
If we select two slices of the pizza, it will be $\frac{2}{8}$ of the pizza. Similarly, if we take six slices of this pizza, it would be $\frac{6}{8}$ of the pizza.
The number on the top of the line is called the numerator. It tells us how many equal parts of the whole are taken. The number below the line is called the denominator. It shows the total number of equal parts the whole is divided into.
Majorly, there are three types of fractions.
Proper fractions: When the numerator of a fraction is less than its denominator, it is a proper fraction. This can also be described as a fraction less than 1 whole. For example, ⅙, ⅜, ⅘ are proper fractions.
Improper fractions: When the numerator of a fraction is more than or equal to its denominator, it is called an improper fraction. For example, 4/3, 8/5, 6/4 are improper fractions.
Mixed fractions: Mixed fractions consist of a whole number along with a proper fraction. For example, $3\frac{4}{7}$, $4\frac{2}{5}$ are mixed fractions.
Recommended Games
What Are Fractions Less than One?
In a fraction, the denominator represents the total number of equal parts the whole is divided into and the numerator is the equal part of the whole selected. In other words, the denominator represents the whole and the numerator represents the selected part of the whole. If the numerator of the fraction is less than the denominator, then it is a fraction less than one whole. For example, if a pizza is equally divided into 6 slices, then one slice is less than the whole pizza (or 6 slices). Since one slice is ⅙ of the pizza, then ⅙ is a fraction less than 1.
When the numerator of a fraction is less than its denominator, then it is fraction less than 1 whole. It is called a proper fraction. The value of a proper fraction is always less than 1. Examples of fraction less than 1 are
Recommended Worksheets
Proper Fractions on a Number Line
A proper fraction or a fraction less than 1 has a value between 0 and 1. So, what is fraction less than one on a number line? It is a fraction that lies between 0 and 1 on a number line. When marking any fraction on the number line, we first look at the denominator. This tells us how many parts we need to divide each number interval.
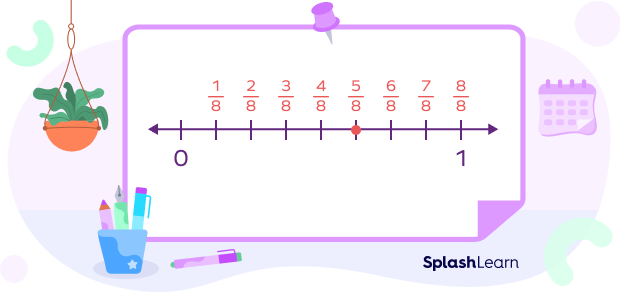
Suppose we wanted to place ⅝ on the number line. We divide the interval between 0 and 1 into 8 equal parts.
The numerator tells us where we place our dot. The following figure shows the fraction ⅝ on a number line.
How Do You Convert Proper Fractions to Decimals?
The value of a proper fraction is always between 0 and 1. To convert fraction less than 1 into decimals, we divide the numerator by the denominator using long division method. As the numerator is smaller than the denominator, first add ‘0’ in the quotient. Place the decimal point after the dividend and after zero in the quotient. Then divide the number with the denominator and get the required answer in decimal.
For instance, let’s convert $\frac{2}{5}$ into decimal form.
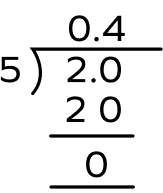
Thus, the fraction $\frac{2}{5}$ is equal to decimal 0.4.
To find the decimal form of a fraction, we can find the fraction into an equivalent fraction with denominator 10, 100 or 1000.
For example, $\frac{2}{5}$ = $\frac{2 ✕ 2}{5 ✕ 2}$ = $\frac{4}{10}$ = 0.4
Note that this method is suitable only for the fractions whose denominator can be converted to a power of 10. For denominators that cannot be written as a power of 10—for example, $\frac{4}{7}$—we can use the long division method.
Solved Examples
Example 1: Identify the fraction less than 1 whole from the following.
$\frac{4}{5}$, $\frac{7}{4}$, $\frac{3}{7}$, $\frac{5}{7}$
Solution: If the numerator of the fraction is less than the denominator, then it is a fraction less than 1. These fractions are also called proper fractions.
In the given fractions, $\frac{4}{5}$, $\frac{3}{7}$, and $\frac{5}{7}$ has a numerator smaller than the denominator. So, these fractions are proper fractions, which have values less than 1.
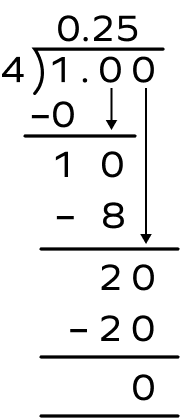
Example 2: Convert 14 into decimal form.
Solution:
Method 1: To convert the fraction into a decimal, we can divide the numerator by the denominator
Method 2: Convert the fraction into an equivalent fraction with denominator power of 10, ie. 10, 100 or 1000.
Here $\frac{1}{4}$ = $\frac{25}{100}$ = 0.25
So, the fraction 1/4 is equal to decimal 0.25.
Example 3: Is the sum of the fractions $\frac{1}{7}$ and $\frac{5}{7}$ less than 1?
Solution: The sum of the fractions $\frac{1}{7}$ and $\frac{5}{7}$ = $\frac{1}{7}$ + $\frac{5}{7}$ = $\frac{6}{6}$
Since the numerator of the sum is less than the denominator, the sum is less than 1.
Practice Problems
Fraction Less Than One - Definition With Examples
Determine which of the following is correct regarding fractions less than one?
1. Fractions less than one are called improper fractions.
2. In a number line, proper fractions lie between 0 to 1.
Fractions less than one are called proper fractions.
The value of a proper fraction is always less than 1. On a number line, they lie between 0 to 1.
Which of the following is correct?
1. The decimal form of $\frac{6}{9}$ is 0.66
2. The decimal form of $\frac{3}{4}$ is 0.7
If we divide 6 by 9, then the answer will be 0.66.
If we divide 3 by 4, then the answer will be 0.75.
The fraction $\frac{4}{9}$ on a number line will be in between which two numbers?
The fraction is a proper fraction. The value of a proper fraction is always between 0 and 1, which is also between 0 and 2.
Frequently Asked Questions
What is the difference between fractions greater than one and fractions less than one?
When a fraction’s numerator is greater than its denominator, the fraction is greater than one. These are also called improper fractions. These fractions lie on the right side of 1 on the number line.
When the numerator of the fraction is less than its denominator, the fraction is less than one. These are also called proper fractions. These fractions lie between 0 and 1 on the number line.
Can 0 be the denominator of fractions less than 1?
No, we cannot have 0 in the denominator of fraction. If we ever have 0 in the denominator, we can say that the fraction is “undefined”.
Is the sum of two proper fractions always a fraction less than one?
Sometimes but not always. For example, $\frac{3}{8}$ + $\frac{2}{8}$ = $\frac{5}{8}$, which is a proper fraction or fraction less than 1. But $\frac{3}{8}$ + $\frac{7}{8}$ = $\frac{10}{8}$, which is not a proper fraction or fraction less than 1.




































