Multiplying Fraction With Whole Numbers

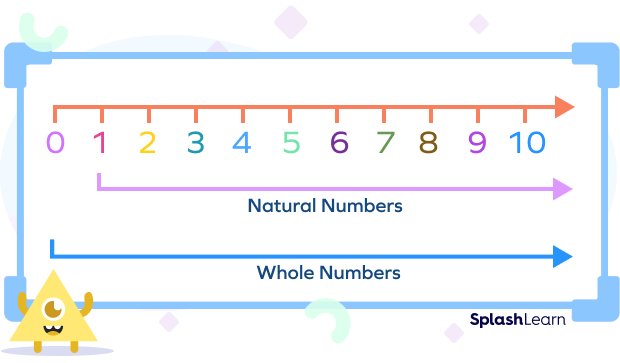
What Are Whole Numbers?

Whole numbers are the set of numbers that includes all natural numbers along with 0. For example, 10, 18, 200, etc. 

What Is a Fraction?

Fractions are often referred to as a number between numbers. Fractions are numerical values that represent a part or a portion of a whole. For example, look at the pizza below.

This pizza has been cut into 4 equal parts. So each piece of the pizza represents 1 out of 4 equal parts. So, mathematically, we can represent each piece as  $\frac{1}{4}$. This number is called a fraction. 

In general, when a whole is divided into equal parts, each part represents a fraction of the whole and we write fractions as $\frac{a}{b}$, where a and b are real numbers and b cannot be zero.

The number below the bar, which represents the total number of equal parts that the whole is divided into, is called the denominator. And the number on the top, which represents the number of equal parts we are considering, is called the numerator. 

Multiplying Fractions with Whole Numbers

Multiplying two numbers is the same as repeated addition. For example,

2 times 4 or $2 \times 4$ is the same as adding the number “4” 2 times.

So, multiplying fractions with whole numbers is the same as repeated addition, where we add the fraction the same number of times as the whole number. 

For example: Let’s try multiplying 3 and $\frac{1}{4}$. 

3 times $\frac{1}{4}$ means adding the fraction $\frac{1}{4}3$ times.

Algebraically this means,

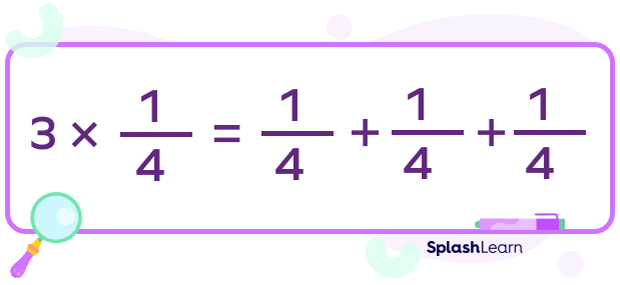
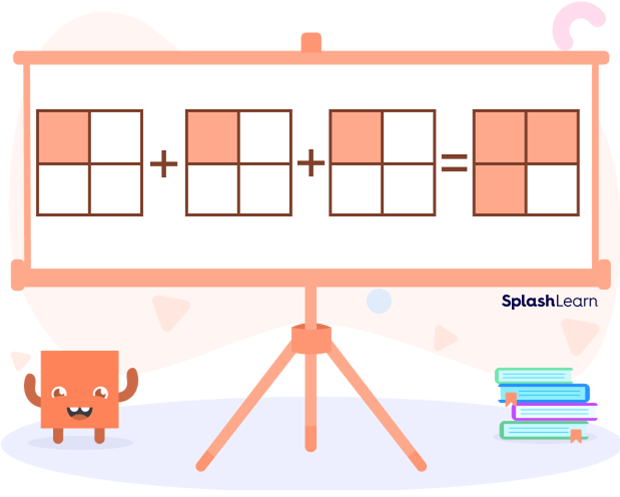
We can solve this expression visually, 

Source 

And our answer will be:

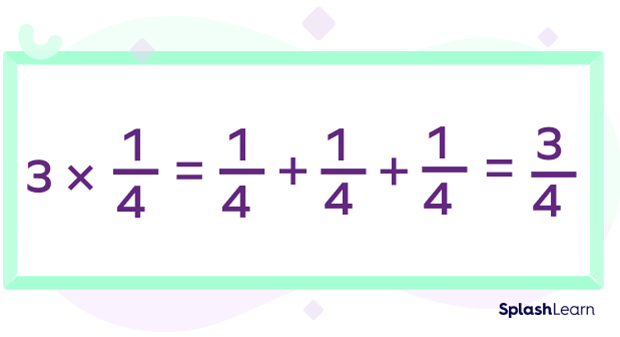
But now, let’s see how we can generalize this without having to make a model every time we want to multiply a whole number and a fraction.

Multiplying Fractions with Whole Numbers

Let’s do this with the help of an example,

Let’s multiply 5 and $\frac{3}{4}$. 

Step 1: Convert 5 into its fraction form by applying 1 in the denominator. 

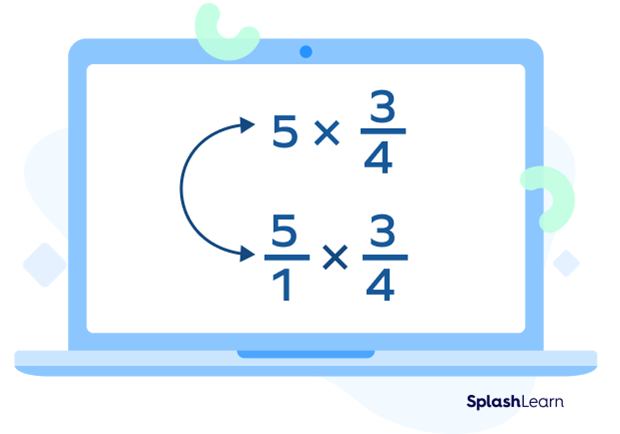
Step 2: Multiply the numerator with the numerator and the denominator with the denominator.

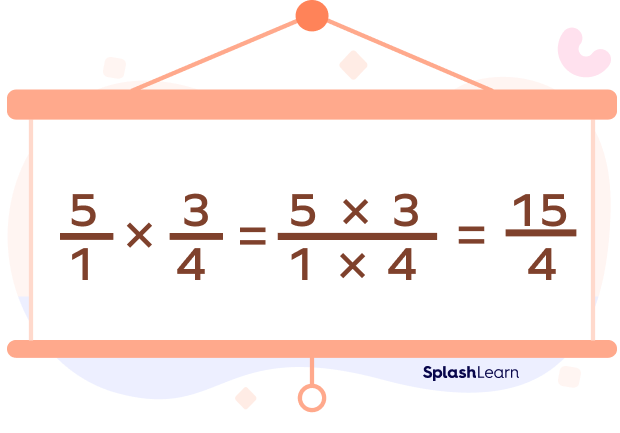
And voila, we have our answer.
As an additional step, if you get an improper fraction you can convert this into a mixed number.

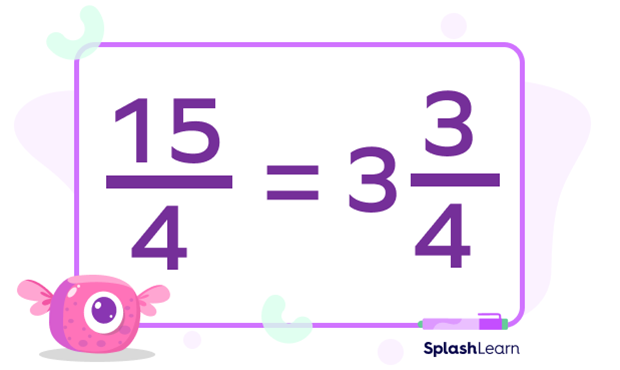
Multiplying Mixed Fractions with Whole Numbers

Multiplying mixed numbers and whole numbers follows the same procedure, only with an extra step.

Let’s do this with the help of an example.

How do we multiply 3 and $2\frac{1}{5}$?

Step 1: Convert the mixed number into an improper fraction.

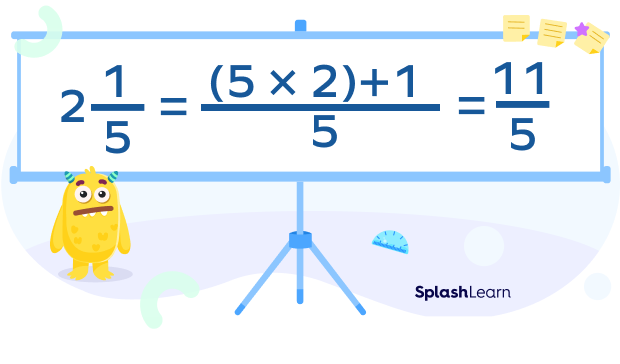
Step 2: Convert 3 into its fraction form by applying 1 in the denominator. 

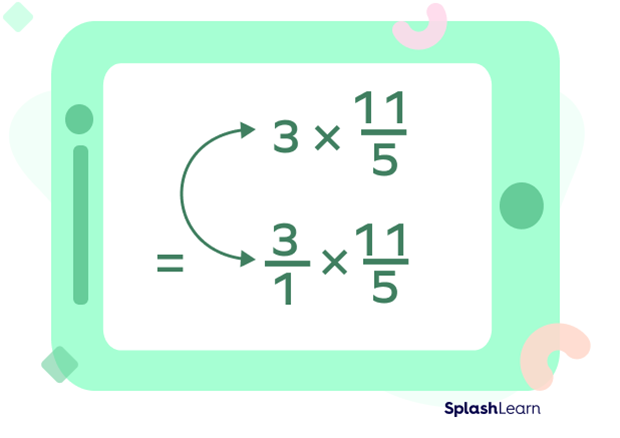
Step 2: Multiply the numerator with the numerator and the denominator with the denominator.

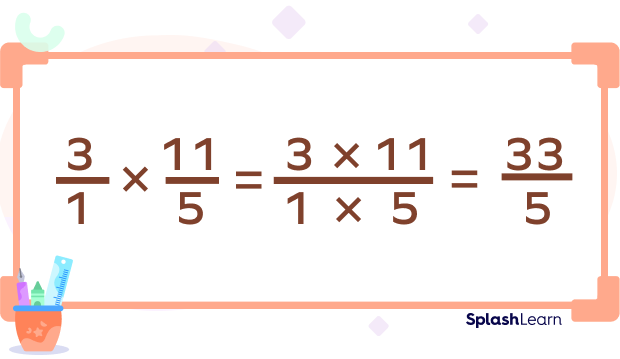
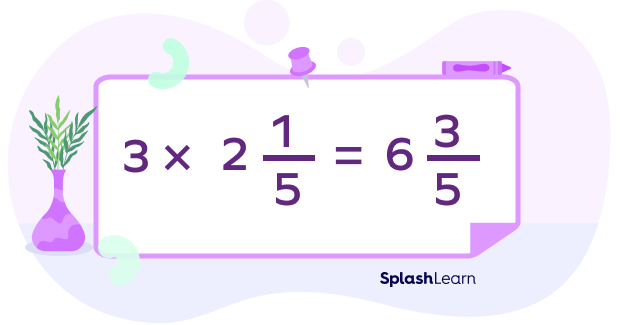
And after converting this into an improper fraction, 

We have our answer:

Solved Examples

Example 1: Catherine is making a cake, for which she needs to use three-fourths of a cup of butter. If she decides to make three cakes, what would be the amount of butter required?

Solution: 

Number of cakes $= 3$ 

Butter required for 1 cake $= \frac{3}{4}$ cups

Total amount of butter required $= 3 \times {3}{4} = \frac{9}{4} = 2\frac{1}{4}$ cups

Example 2: Find the product of the whole number 10 and the mixed fraction 523. Solution: $10\times 5\frac{2}{3} = 10 \times \frac{17}{3} = \frac{170}{3} = 56\frac{2}{3}$

Practice Problems

Frequently Asked Questions