Definition of Multiplying Fractions
By multiplying fractions we mean the product of a fraction with another number or a fraction.
The product of such multiplication could be a fraction or a whole.
Steps to Multiply Fractions
- Fraction by Fraction
Follow these steps to multiply two fractions (either proper or improper):
STEP 1: Multiply the numerators
STEP 2: Multiply the denominators
STEP 3: Simplify the product in the lowest form
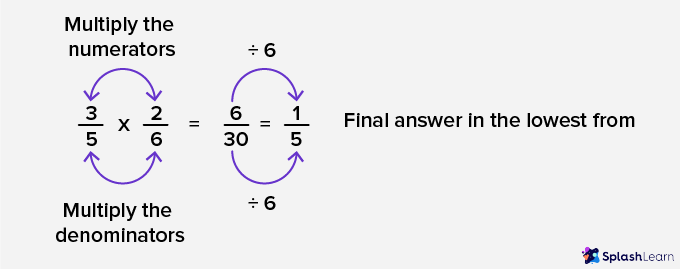
Unlike addition and subtraction, any two fractions with different denominators can easily be multiplied. We just need to multiply both the denominators for the denominator of the product.
Quick Tip: In case, any of the multiplicands are mixed numbers, we first convert them into improper fractions and then follow the steps mentioned above.
- Fraction by Whole Number
Follow these steps to multiply a fraction (either proper or improper) by a whole number:
STEP 1: Multiply the numerator with the whole number.
STEP 2: The denominator remains the same.
STEP 3: Simplify the product in the lowest form.
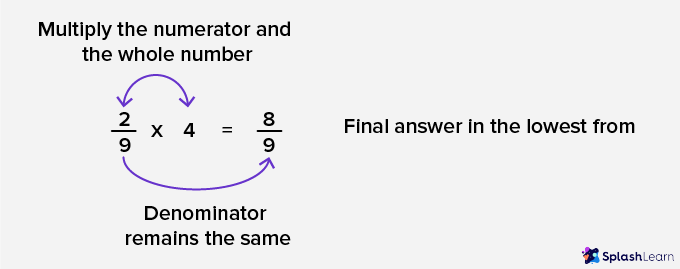
Quick Tip: The denominator remains the same because the denominator of a whole number, when written in fraction form, is 1.
Recommended Games
Representing Multiplication of Fractions Using Models
Let’s represent the product: $\frac{2}{5} \times \frac{3}{4}$; using models.
Finding $\frac{2}{5} \times \frac{3}{4}$ is equivalent to finding $\frac{2}{5} of \frac{3}{4}$.
That is, we will first show three-fourths and then shade two-fifths of it.
Step 1: Divide a rectangle into 4 equal parts and shade 3 parts red to represent $\frac{3}{4}$.
Step 2: Next, divide each box into 5 equal parts.
Step 3: Shade 2 parts green in each of the 3 red-shaded parts. This would represent $\frac{2}{5}$ of each red box.
Step 4: Identify the fraction represented by green boxes.
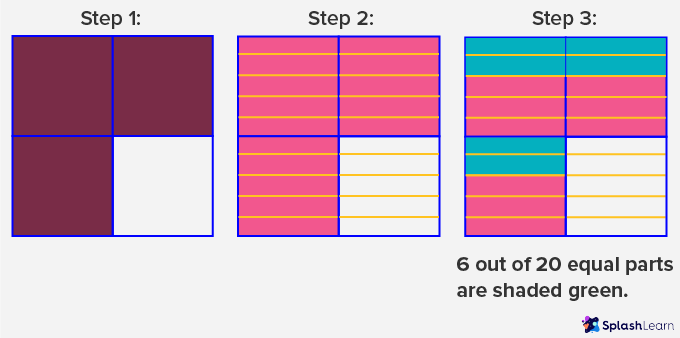
We got 6 shaded parts in green out of the 20 total parts. So, $\frac{2}{5} \times \frac{3}{4}$ = $\frac{6}{20}$.
Now let’s verify the answer using the steps mentioned in the previous section.
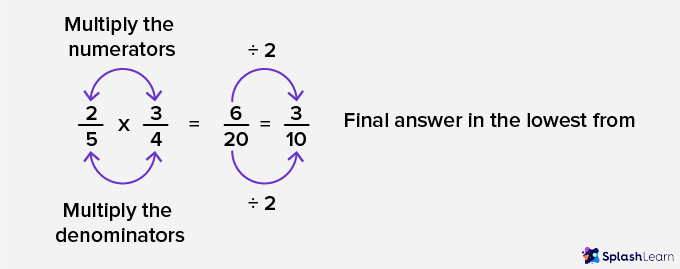
So, we got the same result through the model, just that it was not in the lowest form.
Recommended Worksheets
Multiplying Fractions as Repeated Addition
Imagine having 5 slices of a watermelon where each slice represents one-fourth of the watermelon.

What fraction of the watermelon do these slices represent?
We have 5 slices of one-fourth of a watermelon. This means we have 5 × $\frac{1}{4}$ of a watermelon.
Now, to find 5 × 14 we can add 14 repeatedly for 5 times. That is,
5 × $\frac{1}{4} = 14 + 14 + 14 + 14 + 14 = 1 + 1 + 1 + 1 + 14 = \frac{5}{4} = 1\frac{1}{4}$
So, 5 quarter slices of a watermelon represent $\frac{5}{4}$ or $1\frac{1}{4}$ of the watermelon.
However, the repeated addition that we used will not always be a feasible way of calculating the product.
Properties of Multiplying Fractions
- When you multiply two fractions, the product of their numerators becomes the numerator of the final product, whereas the product of the denominators becomes the denominator of the final product.
- If the product of two fractions is 1, they are said to be the multiplicative inverse or reciprocal of each other. For example, $\frac{4}{7}$ and $\frac{7}{4}$ are multiplicative inverse or reciprocal of each other because $\frac{4 \times 7}{7 \times 4}$ = $\frac{28}{28}$ = 1.
- Multiplying a non-zero fraction by 1 gives the product as the fraction itself. That is $\frac{4}{7} \times 1 = \frac{4}{7}$.
Solved Examples
Example 1: Solve: $\frac{4}{6} \times \frac{3}{2}$ (Multiplying Two Fractions)
Solution: $\frac{4}{6} \times \frac{3}{2} = \frac{4 \times 3}{6 \times 2} = \frac{12}{12}$ = 1
Example 2: Solve: $12 \times \frac{3}{4}$ (Multiplying Whole Number with Fraction)
Solution: $12 \times \frac{3}{4} = \frac{12 \times 3}{4} = \frac{36}{4} = 9$
Example 3: Solve: 5$\frac{1}{2} \times 2\frac{1}{4}$ (Multiplying Two Mixed Numbers)
Solution: 5$\frac{1}{2} \times 2\frac{1}{4} = \frac{(2 \times 5) + 1}{2} + \frac{(2 \times 4) + 1}{4} = \frac{11}{2} \times \frac{9}{4} = \frac{99}{8} = 12\frac{3}{8}$
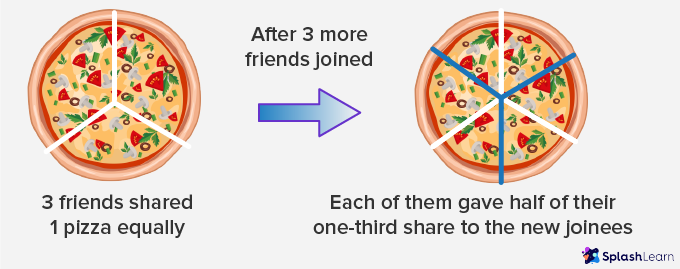
Example 4: A group of 3 friends equally divided a pizza among themselves. Later 3 more friends joined them. So, they decided to give half of their share to the new joiners. What fraction of pizza did each one of them get?
Solution:
Before 3 friends joined the group: 3 friends shared one pizza equally
Fraction of pizza shared by each friend = $\frac{1}{3}$
After 3 more friends joined the group: Every 3 friends gave half of their share.
Fraction of pizza shared by each friend = $\frac{1}{2} \times \frac{1}{3}$
= $\frac{1}{6}$ of the pizza.
So, each of them got one-sixth of the pizza.
The picture given below depicts the situation discussed above.
Practice Problems
Multiplying Fractions1 What is the product of $\frac{5}{3}$ and $\frac{2}{20}$?$\frac{10}{20}$ $\frac{10}{30}$ $\frac{5}{60}$ $\frac{1}{6}$ CorrectIncorrect Correct answer is: $\frac{1}{6}$ $\frac{5}{3} × \frac{2}{20}? = 5 × \frac{2}{3}? × 20 = \frac{10}{60}? = \frac{1}{6}$ 2 What is the product of 16 and $\frac{25}{8}$?50 12$\frac{1}{2}$ $\frac{1}{50}$ $\frac{41}{8}$ CorrectIncorrect Correct answer is: 50 16 × $\frac{25}{8}$ = 2 × $\frac{25}{1}$ = $\frac{50}{1}$ = 50 3 Multiplying $\frac{13}{12}$ by what fraction will result in 1?$\frac{-13}{12}$ $\frac{-12}{13}$ $\frac{12}{13}$ $\frac{13}{12}$ CorrectIncorrect Correct answer is: $\frac{12}{13}$ $\frac{13}{12} × \frac{12}{13} = \frac{156}{156}$ = 1 |




































