Introduction to Quarter in Math
Mathematics is not just a subject of units and numbers. Math concepts are regularly applied in our daily lives. We don’t even realize how mathematical laws rule everything we see in our surroundings.
Today, we will discuss an interesting topic: a quarter!
A quarter is a mathematical fraction frequently used while measuring or calculating portion, time, money, etc.
Fraction is defined as the part of a whole. Fraction is not only used in math problems but in real life frequently. This article will take a detailed look into a commonly used fraction: one-fourth.
One-fourth or a quarter is a mathematical fraction often used while measuring or calculating portion, time, money, etc. Let’s dive right into it.
Recommended Games
What Is a Quarter in Math?
Let’s look at the quarter definition in math.
A quarter can be explained as one part of four equal parts. If you take one whole unit, it is made up of four quarters.
A quarter is represented by using fractions in mathematics.
In mathematical terms, a quarter fraction is the division of 1 whole into 4 equal parts, where 1 denotes the part that is referred to and 4 represents the number of parts into which the whole has been divided.
In numerical form, it is written as ¼.

Let’s take an example to understand what’s a quarter in numbers.
For example, to find the quarter of 8 peaches, you need to divide them into 4 equal parts.
Each part will have 2 peaches. A quarter is what each equal part represents.
So, the quarter of 8 is 2.
Recommended Worksheets
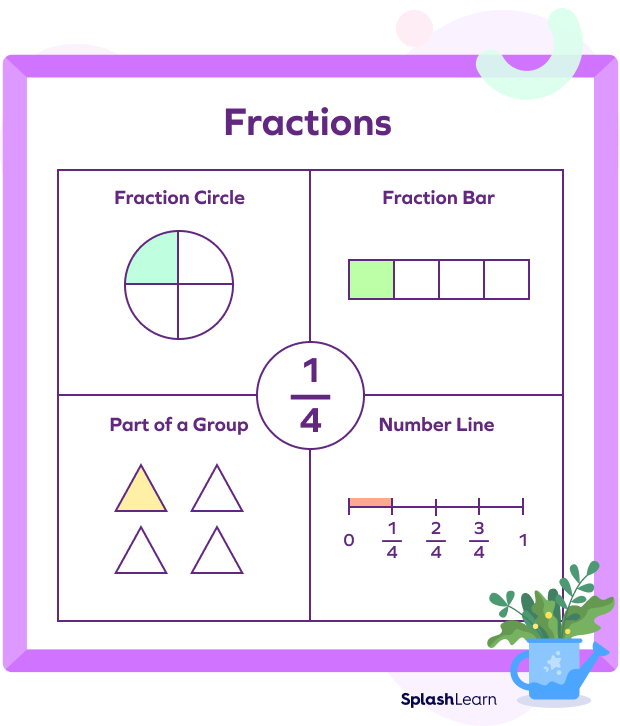
What Is One-fourth in Math?
We split one whole into four equal parts. One out of four equal parts of the whole is known as one-fourth. It is also known as a quarter. In numerical form, it is written as $\frac{1}{4}$.
Let us look at an example. A cake is divided into 4 equal parts. If the whole cake represents 1, then each piece is one-fourth of the whole. The entire cake is made up of 4 one-fourths (or 4 quarters).
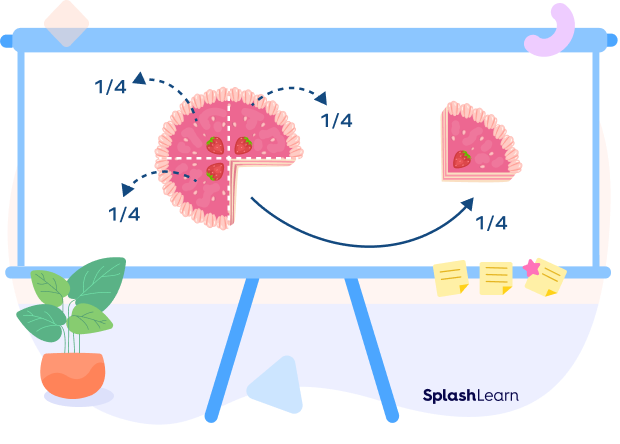
Let’s look at one-fourth of a shape. We can represent the fraction, one-fourth, in different ways, as shown in the figure below.
One-fourth or ¼ can also be written as 0.25 and 25%.
One-fourth of a Number
What Is One-fourth of a Whole Number?
One-fourth is the same as the fraction $\frac{1}{4}$. It means that in order to find one fourth of a number, we have to divide the number by 4. In order to do this, we simply divide or split our whole number into 4 equal parts.
For example, to calculate a quarter of 28, we can divide 28 by 4. As a calculation, it would look like $28 \div 4$, which is equal to 7. It means that one-fourth of 28 is 7.
What Is One-fourth of a Fraction?
One-fourth of any fraction is the same as multiplying $\frac{1}{4}$ and the fraction. We get the answer by multiplying the numerator together and the denominators together.
For example, let’s see what one fourth of ¼ is. Well, it is the same as multiplying the fraction together. So, $\frac{1}{4}$ of $\frac{1}{4} = \frac{1}{4} \times \frac{1}{4} = \frac{1}{16}$
One-fourth in Real Life
Let’s look at some real-life examples of one-fourth.
- Time, such as a $\frac{1}{4}$ of an hour. You can divide 1 hour, that is 60 minutes, by 4. So, $\frac{1}{4}$ of an hour is 15 minutes.
- The year, such as $\frac{1}{4}$ of a year. You can divide 1 year, that is 12 months, by 4. This means $\frac{1}{4}$ of a year is 3 months.
- Money, such as $\frac{1}{4}$ of a dollar. 100 cents make 1 dollar. So, $\frac{1}{4}$ of a dollar would be 25 cents.
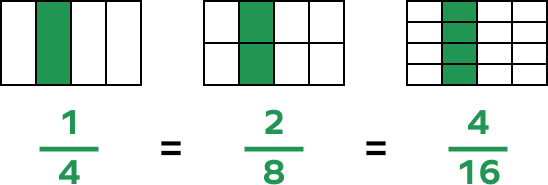
Fractions Equivalent to One-fourth
It is not compulsory that you will always find one fourth written as $\frac{1}{4}$. You can also find it written in its equivalent fractions form. In order to find a fraction equivalent to $\frac{1}{4}$, we just need to multiply the numerator and denominator by natural numbers.
$\frac{1}{4} = \frac{1 \times 2}{4 \times 2} = \frac{1 \times 3}{4 \times 3} = \frac{1 \times 4}{4 \times 4}$ and so on.
So, $\frac{1}{4} = \frac{2}{4} = \frac{3}{4} = \frac{4}{16}$

Using Quarter in Various Forms
A quarter in math can be used to represent various things:
- Time, such as a quarter of an hour. You can divide 1 hour, that is 60 minutes, by quarter:
There are 15 minutes in one quarter. Therefore, “quarter to 4” or “quarter past 4” denotes the time to be 3:45 and 4:15, respectively.

- The year, such as a quarter of a year. You can divide 1 year, that is 12 months, by 4 (a quarter). This means each quarter includes 3 months.
- Quarter 1 – January 1 to March 31
- Quarter 2 – April 1 to June 30
- Quarter 3 – July 1 to September 30
- Quarter 4 – October 1 to December 31

- Money, such as a quarter of a dollar. 100 cents make 1 dollar. So, a quarter of a dollar would be 25 cents.

Fun Fact!
- The term quarter is also a name used for one of McDonald’s popular burgers, the “Quarter Pounder.” The burger contains a patty that weighs ¼ pound in its precooked state, which is the reason behind this name.
Solved Examples
Example 1: Write the quarter of 32 and state how many 4s are in the number 32?
Solution:
$\frac{32}{4} = 8$
or,
$\frac{1}{2} \times 32 = 16$
$\frac{1}{2} \times 16 = 8$
Example 2: Calculate the quarter of 68.
Solution:
$\frac{1}{4} \times 68 = 17$
Example 3: Sunny has a quarter of 48 muffins, and Harry has half of 24 muffins. Find out who has more muffins.
Solution:
Quantity of muffins Sunny has $= \frac{1}{4} \times 48 = 12$
Quantity of muffins Harry has $= \frac{1}{2} \times 24 = 12$
Therefore, both Sunny and Harry have an equal number of muffins, i.e., 12 muffins.
Example 4. What is one-fourth of 96?
Solution: One fourth of $96 = \frac{1}{4} \times 96 = 96 \div 4= 24$.
Example 5. Area of a rectangle is 124 $cm^{2}$. $\frac{1}{4}$ of the rectangle is painted blue. What is the area of the rectangle that is painted blue?
Solution: Total area of rectangle $= 124$ $cm^{2}$
Area of rectangle that’s painted blue $= \frac{1}{4} \times 124 = 31$ $cm^{2}$
Example 6. Emma took 40 red pearls out of 160 pearls. What percent of the whole did she take?
Solution: Total number of pearls $= 160$
Number of pearls Emma took $= 40$
Fraction $= \frac{40}{160} = \frac{1}{4}$
$\frac{1}{4}$ in percentage $= \frac{1}{4} \times 100 = 25%$
Emma took $25%$ of the pearls.
Practice Problems
Quarter – Definition with Examples
Calculate the quarter of 20.
As we know, a quarter of anything is $\frac{1}{4}$ of anything.
Therefore,
$\frac{1}{4} \times 20 = 5$
Thus, the answer is ‘5’.
The diameter of a circle is 32 cm. Calculate the area of a quarter circle.
Diameter of the circle $= 32$ cm
Total area of a quarter circle $= \frac{\pi d^{2}}{16}$
$= \frac{22}{7} \times \frac{1}{16} \times 32^{2}$
$= 201.14$ $cm^{2}$
Note:
When the length of radius $= r$
The length of diameter (d) of the circle $= 2r$
Therefore, $r = \frac{d}{2}$.
Area of the circle $= \pi (\frac{d}{2})^{2}$
$= \frac{πd^{2}}{4}$
Thus, area of quarter circle $= 14 × \pi (\frac{d}{2})^{2}$
$= \frac{\pi d^{2}}{16}$
Eric invited 52 guests for his birthday party. However, only a quarter of the entire guest list arrived. Calculate how many guests attended the party.
Number of guests invited to the party $= 52$
Number of guests attended the party $= \frac{1}{4} \times 52$
$= 13$
Mary bought 24 apples from the store. A quarter of them were rotten and had to be discarded. How many fresh apples are remaining?
Number of apples bought $= 24$
Number of apples that were rotten $= \frac{1}{4} \times 24$
$= 6$
Number of fresh apples left $= 24$ $–$ $6$
$= 18$
Which of the following figure does not represent 0.25?
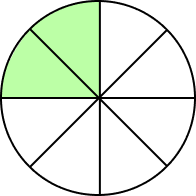
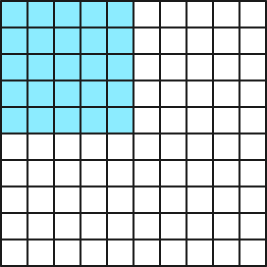
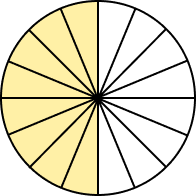

In option C, the number of shaded parts are 8 and total number of parts are 16.
So, the fraction will be $\frac{8}{16} = \frac{1}{2} = 0.5 \neq 0.25$
Mia bought 32 apples from the store. $\frac{1}{4}$ of them were rotten and had to be discarded. How many fresh apples are remaining?
$\frac{1}{4}$ of $32 = 8$. So, the number of fresh apples $= 32$ $-$ $8 = 24$.
Which of the following is equal to $\frac{1}{4}$ of $\frac{1}{2}$ ?
$\frac{1}{4}$ of $\frac{1}{2} = \frac{1}{4} \times \frac{1}{2} = \frac{1}{8}$
Frequently Asked Questions
What is the meaning of three quarters?
A quarter is one-fourth of a whole number, and numerically it is represented as $\frac{1}{4}$. Three quarters mean $\frac{1}{4} \times 3$ or $\frac{3}{4}$.

What are some of the equivalent fractions of a quarter?
$\frac{1}{4} = \frac{2}{8} = \frac{3}{12} = \frac{4}{16} = \frac{5}{20} = \frac{6}{24}$, and so on
How many minutes can be calculated from a quarter of an hour?
A quarter of an hour means 15 minutes.One hour means 60 minutes, and a quarter of 60 minutes is thus $\frac{1}{4} \times 60 = 15$
Is $\frac{1}{4}$ a rational number?
Yes. The decimal representation of $\frac{1}{4}$ is 0.25. As it is a terminating decimal number, we can say that $\frac{1}{4}$ is a rational number.
What is the difference between four and one-fourth?
The number 4 represents four wholes. For example, 4 children are playing in the park. 4 is a natural number. $\frac{1}{4}$ means part of a whole. It is not a natural number.
What is the difference between fourth and one-fourth?
Ordinal numbers are numbers that are used to represent the “order” or are used to define a thing’s position.Fourth as an ordinal number can be written as “4th.” It is used to describe the ordinal number between third (3rd) and fifth (5th). Whereas one-fourth means part of a whole. It is represented by the number $\frac{1}{4}$.




































