What Does “Subtracting Fractions” Mean?
Subtracting fractions is finding the difference between the two or more fractions with the same or different denominators.
Subtracting like fractions (fractions with same denominators) is a simple and straightforward process, but in order to subtract unlike fractions (fractions with different denominators), we first need to make the denominators the same.
Fraction subtraction is a very important math skill that we constantly use in day-to-day life. Let’s consider some real-life scenarios to understand the significance of subtracting fractions.
Example 1: Subtracting like fractions
Your daily exercise goal includes running $\frac{3}{4}$ miles. If you have already run $\frac{1}{4}$ miles in the morning, you need still need to run $\frac{3}{4} – \frac{1}{4}$ miles to complete your goal.
Example 2: Subtracting unlike fractions
Suppose you need to add $\frac{3}{4}$ cups of water in a curry. You already added half a cup of water. Now, to determine how much more water you need to add in the curry, you need to subtract $\frac{1}{2}$ from $\frac{3}{4}$.
Recommended Games
How to Subtract Fractions
When subtracting fractions, we come across following cases:
- Subtracting Fractions with Like Denominators
- Subtracting Fractions with Unlike Denominators
- Subtracting Mixed Fractions
- Subtracting Fractions with Whole Numbers
The process of subtracting fractions in each of these cases is somewhat similar, except for the few steps depending on the type of fractions.
Recommended Worksheets
Subtracting Fractions with Same Denominators
Fractions with the same denominator are called “like fractions.”
To subtract like fractions, follow these steps:
Step 1: Subtract the numerators.
Step 2: Keep the denominator as it is.
Step 3: Reduce the fraction to the simplest form, if necessary.
Example 1: Let’s solve the previous example.
To complete your exercise goal, you need to run $\frac{3}{4} – \frac{1}{4} miles.
$\frac{3}{4} – \frac{1}{4} = \frac{3\; – \;1}{4} = \frac{2}{4} = \frac{1}{2}$
So, you need to run half a mile more to complete the goal.
Example 2: $\frac{9}{11} – \frac{5}{11}$
$\frac{9}{11} – \frac{5}{11} = \frac{9 \;-\; 5}{11} = \frac{4}{11}$
Example 3: $\frac{9}{13} – \frac{5}{13} – \frac{1}{13}$
$\frac{9}{13} – \frac{5}{13} – \frac{1}{13} = \frac{9 \;- \;5 -\;1}{13} = \frac{3}{13}$
OR
$\frac{9}{13} – \frac{5}{13} – \frac{1}{13}$
$= \frac{9 – 5}{13} – \frac{1}{13}$ …focus on the first two fractions
$= \frac{4}{13} – \frac{1}{13}$ …now subtract the third fraction
$= \frac{3}{13}$
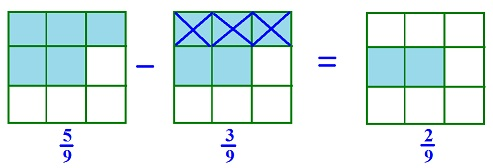
Example $4: \frac{5}{9} – \frac{3}{9} = \frac{2}{9}$
We can represent this subtraction visually as:
Subtracting Fractions with Unlike Denominators
Fractions with different denominators are called “unlike fractions.” To subtract unlike fractions, we first convert them into like fractions by finding their common denominator.
The easiest way to convert unlike fractions into like fractions is the LCM method.
Follow these steps:
Step 1: Find the LCM of the two denominators.
Step 2: Find the equivalent fractions of the given two fractions, such that the denominator of these new fractions equals the LCM value.
We do this by multiplying and dividing both numerator and denominator by an appropriate number.
Step 3: Now that we have two like fractions (which are basically the equivalent fractions of the original fractions), we follow the steps for subtracting like fractions.
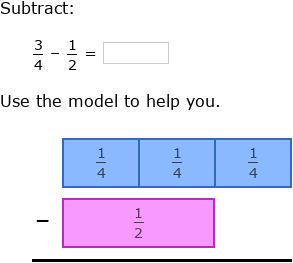
Example 1: Let’s recall the real-life example we discussed. You need to add $\frac{3}{4}$ cups of water in a curry. You have added $\frac{1}{2}$ a cup of water. Subtract $\frac{1}{2}$ from $\frac{3}{4}$ to find the amount of water you still need to add as per the curry recipe.
i) Note that subtracting $\frac{1}{2}$ from $\frac{3}{4}$ means finding the value of $\frac{3}{4} – \frac{1}{2}$.
$\frac{1}{2}$ from $\frac{3}{4}$ are unlike fractions since the denominators are not equal.
Let’s find the common denominator.
LCM(2, 4) = 4
ii) We need to find the equivalent fractions of $\frac{1}{2}$ from $\frac{3}{4}$ whose denominator is 4.
$\frac{1}{2} = \frac{1 \times 2}{2 \times 2} = \frac{2}{4}$
The denominator of $\frac{3}{4}$ is already 4.
iii) Now, we have $\frac{2}{4}$ and $\frac{3}{4}$, which are like fractions.
Thus, we redefine the problem as
$\frac{3}{4} – \frac{1}{2} = \frac{3}{4} – \frac{2}{4} = \frac{3 – 2}{4} = \frac{1}{4}$
This, means that you still need to add $\frac{1}{4}$ cup of water in the curry.
Example 2: Subtract $\frac{1}{3}$ from $\frac{2}{5}$.
LCM of 3 and 5 = 15.
$\frac{2}{5} = \frac{2 \times 3}{5 \times 3} = \frac{6}{15}$
$\frac{1}{3} = \frac{1 \times 3}{3 \times 3} = \frac{5}{15}$
$\frac{2}{5} – \frac{1}{3} = \frac{6}{15} – \frac{5}{15} = \frac{1}{15}$
Subtracting Mixed Fractions
A mixed fraction is a fraction that is composed of a whole number and a proper fraction.
For example, $2\frac{4}{5}$ is a mixed fraction.
Each mixed fraction represents a unique improper fraction. Thus, we can always convert a mixed fraction into an improper fraction, and vice versa. This is one of the easiest methods for subtracting mixed fractions.
Here’s how we convert a mixed fraction into an improper fraction.
$q\frac{n}{d} = \frac{qd + n}{n}$
For example, $2\frac{4}{5} = \frac{(2 \times 5) + 4}{5} = \frac{14}{5}$
Example: Subtract $7\frac{1}{3}$ from $12\frac{1}{2}$.
Step 1: Convert the mixed fractions into the improper fraction.
$12\frac{1}{2} = \frac{(2 \times 12) + 1}{2} = \frac{25}{2}$
$7\frac{1}{3} = \frac{(3 \times 7) + 1}{3} = \frac{22}{3}$
Step 2: Check the denominator values of the resulting fractions.
- If the denominators are equal, follow the steps of subtracting fractions with like or same denominators.
- If the denominators are not equal, follow the steps of subtracting fractions with unlike denominators.
In this case, the fractions are unlike.
LCM of 2 and 3 is 6.
$\frac{25 \times 3}{2 \times 3} = \frac{75}{6}$
$\frac{22 \times 2}{3 \times 2} = \frac{44}{6}$
$12\frac{1}{2} – 7\frac{1}{3} = \frac{75}{6} – \frac{44}{6} = \frac{31}{6} = 5\frac{1}{6}$
Subtracting Fractions and Whole Numbers
We can represent any whole number as a fraction with denominator 1. For example, $5 = \frac{5}{1}$.
So, when subtracting fractions from whole numbers, or when subtracting whole numbers from fractions, we first express the whole number as a fraction.
Example: Katherine walks 3 miles to the school. She has already walked $\frac{1}{3}$ km. To determine, the distance she still needs to cover, we will subtract $\frac{1}{3}$ from 3.
Step 1: Convert the whole number into the fractional form.
$3 = \frac{3}{1}$
Step 2: Subtract the two unlike fractions. Write the resulting fraction as a mixed fraction, if necessary.
The LCM of 1 and 3 is 3.
$\frac{3}{1} = \frac{9}{3}$
We get
$\frac{9}{3} – \frac{1}{3} = \frac{9 – 1}{3} = \frac{8}{3} = 2\frac{2}{3}$
Facts about Subtracting Fractions
- Common denominator is the important concept when subtracting two fractions with different denominators. It is a shared multiple of two denominators.
- You can also subtract the mixed fractions without converting them into the improper fractions. Subtract the whole numbers and fractions separately and combine the results.
- Example: $5\frac{2}{5} – 2\frac{1}{5} = (5 – 2) + (\frac{2}{5} – \frac{1}{5}) = 3 + \frac{1}{5} = 3\frac{1}{5}$
Conclusion
In this article, we learned about subtracting fractions, methods of subtracting fractions for different types of fractions, and examples. Let’s solve a few more examples, and practice MCQs based on subtracting fractions.
Solved Examples on Subtracting Fractions
1. Jenny had $\frac{2}{3}$ of a whole pizza and offered the remaining pizza to his sister. What part did her sister get?
Solution:
Part of pizza Jerry had $= \frac{2}{3}$
Part of pizza his sister got $= 1 – \frac{2}{3} = \frac{1}{1} – \frac{2}{3}$
LCM of 1 and 3 is 3.
We get
$\frac{3}{3} – \frac{2}{3} = \frac{1}{3}$
Jenny’s sister got one-third of the pizza.
2. Find: $\frac{4}{5} – \frac{2}{5}$.
Solution:
Denominators are equal.
Fractions are like fractions.
$\frac{4}{5} – \frac{2}{5} = \frac{4 – 2}{5} = \frac{2}{5}$
3. Subtract $5\frac{2}{5}$ from $6\frac{1}{3}$.
Solution:
We have to find $6\frac{1}{3} – 5\frac{2}{5}$.
Converting into improper fractions, we get
$6\frac{1}{3} = \frac{19}{3}$
$5\frac{2}{5} = \frac{27}{5}$
We can rewrite the given problem as
$6\frac{1}{3} – 5\frac{2}{5} = \frac{19}{3} – \frac{27}{5}$
LCM of 3 and 5 = 15
$\frac{19 \times 5}{3 \times 5} = \frac{95}{15}$ and $\frac{27 \times 3}{5 \times 3} = \frac{81}{15}$
$\frac{95}{15} – \frac{81}{15} = \frac{14}{15}$
Practice Problems on Subtracting Fractions
Subtracting Fractions - Definition With Examples
$1 - \frac{1}{5} - \frac{2}{5} =$
$1 - \frac{1}{5} - \frac{2}{5}$
$= \frac{2}{5}$
$= \frac{5}{5} - \frac{1}{5} - \frac{2}{5}$
$= \frac{5 - 1 - 2}{5}$
$= \frac{2}{5}$
Find $\frac{5}{6} - \frac{9}{11}$.
LCM(6, 11) = 66
$\frac{5}{6} = \frac{55}{66}$ and $\frac{9}{11} = \frac{54}{66}$.
Difference $= \frac{55}{66} - \frac{54}{66} = \frac{1}{66}$
$5\frac{7}{12} - 2\frac{3}{4} =$
$5\frac{7}{12} - 2\frac{3}{4} = \frac{67}{12} - \frac{11}{4}$
LCM(12, 4) = 12
$\frac{67}{12} - \frac{11}{4} = \frac{67}{12} - \frac{33}{12} = \frac{67-33}{12} = \frac{34}{12} = \frac{17}{6} = 2\frac{5}{6}$
Subtract the fractions visually.
$\frac{5}{8} - \frac{4}{8} = \frac{1}{8}$
Frequently Asked Questions about Subtracting Fractions
Do the numerators must be the same while subtracting fractions?
While subtracting two or more fractions, the denominator must be the same otherwise we can not subtract the fractions with unlike denominators.
Why do we make denominators the same when subtracting fractions?
The denominator represents the total number of “equal parts” the whole is divided into. To define a fraction, the whole must be divided into equal number of parts. So, in order to define the resulting fraction after subtraction, we must have equal divisions of the whole. So, the denominators of two fractions must be the same.
Can the difference of two fractions be negative?
If you subtract a larger fraction from a smaller fraction, the difference will be negative.




































