What is Arc in Math?
In mathematics, an arc is defined as a portion of the boundary of a circle or a curve. It can also be referred to as an open curve.
The boundary of a circle is the perimeter or the distance around a circle, also known as the circumference. So, the arc is the distance between any two points traced along its circumference.
Let us understand this with the help of an example:
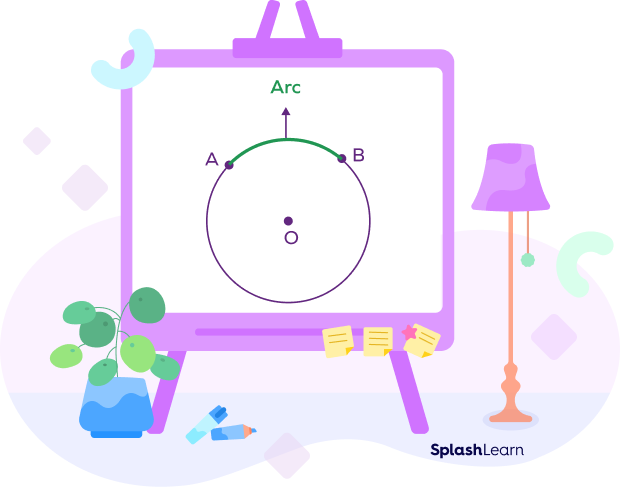
In this figure, the distance between points A and B is an arc traced along the circumference of the circle. You can call it arc AB. An arc is denoted by the symbol “⌢”. So, the arc AB can be written as $\widehat{AB}$. You can also write it as $\widehat{BA}$. The order of the points does not matter.
Recommended Games
How to Make an Arc
To make an arc, you either need a chord or a central angle.
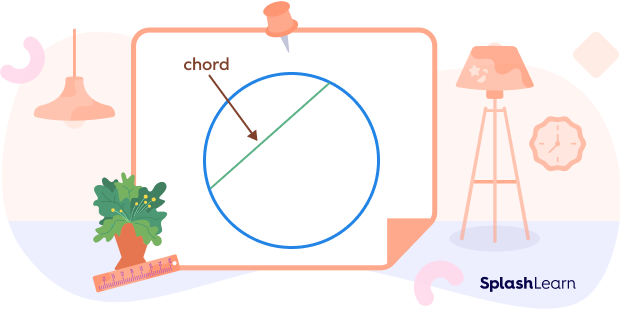
A chord is a line segment that joins any two points on a circle.
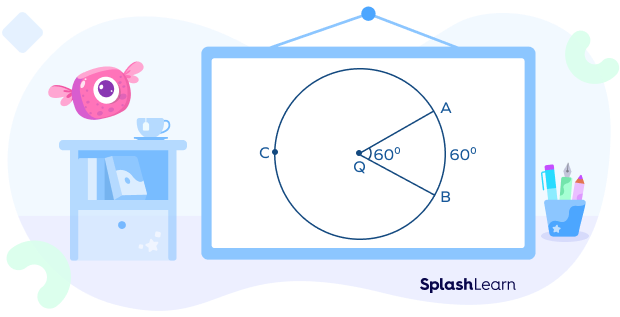
A central angle is an angle between any two radii of the circle. For instance, the central angle in the diagram between the radii QA and QB, as shown below, is 60°.
Types of Arcs
You must have noticed that an arc divides a circle into two parts.
One has a shorter distance between the two endpoints (minor arc), while the other has a longer distance (major arc).
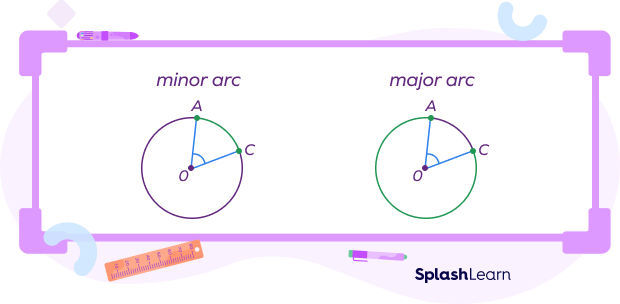
Unless specified, an arc will always be considered a minor arc. To specify the major arc, you can take a third point on the arc of the circle and use three letters in the name.
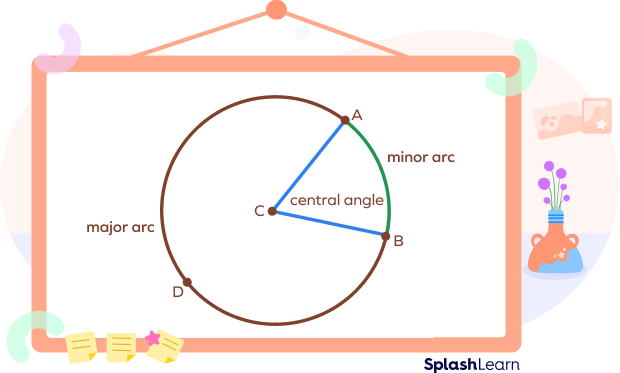
In the diagram above, $\widehat{AB}$ is the minor arc, and $\widehat{ADB}$ is the major arc.
Semicircle Arc
A semicircle is an arc that has its endpoints on the diameter of a circle.
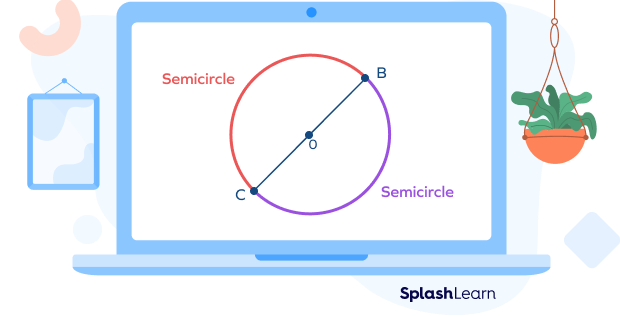
How to Find the Arc Length?
You can calculate the length of an arc by using the formula given below.
Arc length of a circle = $\frac{y}{360}$ ✕ $2 π r$
Where r = the radius of the circle
y = the angle (in degrees) subtended by an arc at the center of the circle
360 = the angle of one complete rotation.
The value of $π$ (pi) = 3.14
Solved Examples
Example 1: Calculate the length of an arc that subtends an angle of 60 degrees at the center of a circle with a radius of 5 cm.
Solution: We know the arc length formula is $\frac{y}{360} ✕ $2 π r$
In this example,
y = 60 and r = 5
Substituting these values in the example, we get
Arc length = $\frac{60}{360}$ ✕ 2 ✕ 3.14 ✕ 5 = 5.23 cm
Example 2: Calculate the length of the arc that subtends an angle of 40 degrees at the center of a circle with a radius of 6 cm.
Solution: We know the arc length formula is $\frac{y}{360}$ ✕ $2 π r$
In this example,
y = 40 and r = 6
Substituting these values in the example, we get
Arc length = $\frac{40}{360}$ ✕ 2 ✕ 3.14 ✕ 6 = 4.186 cm
Example 3: Identify the major arc in this circle.
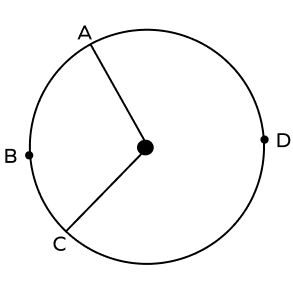
We know that a major arc is a long distance between two endpoints. So here, $\widehat{ADC}$ is the major arc, and $\widehat{ABC}$ is the minor arc.
Practice Problems
Arc - Definition with Examples
Calculate the length of the arc that subtends an angle of 120 degrees at the center of a circle with a radius of 10 cm.
Arc length = $\frac{y}{360}$ ✕ $2 π r$
Substituting y = 120 and r = 10 cm, we get
Arc length = $\frac{40}{360}$ ✕ 2 ✕ 3.14 ✕ 10 = 20.93 cm
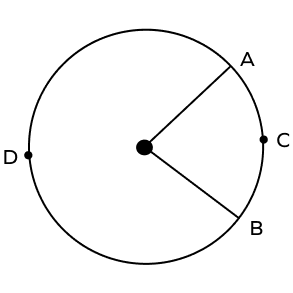
Identify the minor arc in the figure given below.
$\widehat{AB}$ is the minor arc in this diagram.
An arc on the circle is drawn so that it covers a quarter of the circumference. What will be the value of the central angle in this case?
For an arc that spans a quarter of the circle, the radii drawn from its endpoints will be perpendicular to each other.
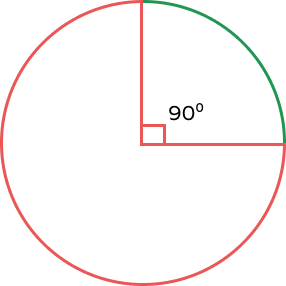
Which of these central angles will create the greatest arc?
The central angle is formed by joining the endpoints of the arc with the center of the circle. Hence, the greater the central angle, the greater will be the length of the arc formed.
Frequently Asked Questions
What is a semicircle arc?
A semicircle is an arc that has its endpoints on the diameter of the circle.
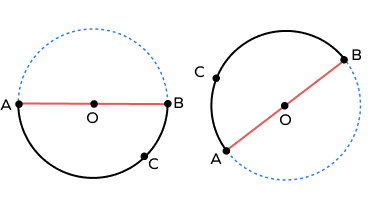
Here, both $\widehat{AB}$ and $\widehat{ACB}$ are semicircle arcs.
What is the central angle of an arc?
A central angle is an angle that an arc subtends at the center.
Can an arc be a straight line?
No. An arc is always an open curve.

















