Central Angle

Introduction to the Central Angle

A central angle is formed when two circle radii form a vertex at the central point of a circle. These arms of the circle may originate at two different points along the arc of such a circle. As a result of their intersection, the two radii form a central angle that helps to segregate a circle into different sectors.

Consider the example of a pizza. Have you noticed how slicing it into different pieces makes it possible to divide one whole pizza into smaller slices? A protractor is another central angle example.

What Is a Central Angle in Geometry?

A central angle is formed at the center of a circle due to the intersection of any two radii within the circle. As stated, a central angle in geometry is one whose vertex forms at the center of the circle, with two radii forming its arms that intersect the circle at two different points.

Joining these two points will yield an arc on the circle. So, we can also say that a central angle is the angle where an arc subtends at the center of a circle. There is no special central angle symbol.

Center Angle of a Circle: Characteristics, Uses, Importance

When a central angle forms at the center of a circle, we can observe certain properties of the figure, such as:

• The measure of the central angle is congruent to the measurement of the arc that it intercepts.
• All congruent central angles form congruent arcs in a circle, and the reverse is also true.
• All congruent central angles form congruent chords in a circle, and the reverse is also true.
• The central angle measures twice the inscribed angle, subtended by the same arc.
• If we were to take measurements of all the central angles of a circle without a common point, the total would come out to $360^\circ$.

Knowledge of the central angle is essential to solve problems relating to angles in a circle. The central angle is essential to calculate the arc length and the sector’s area. With the measure of the central angle in hand, we can easily calculate the other measures related to the angle.

Central Angle Formula

The formula for central angle is calculated using the measure of arc and the inscribed angle of the circle.

The central angle is congruent to the intercepted arc. Thus,

Central angle $=$ Intercepted arc

The central angle is twice the inscribed angle subtended by the same arc. Thus,

Central angle $= 2$ (inscribed angle)

• Central angle $= \frac{Arc Length}{Radius}$
• Central angle $= \frac{2(area of sector)}{(Radius)^2}$ 

We can also denote the central angle formula as follows:

Central Angle $= s \times \frac{360}{2 \pi r}$

Here “s” is the length of the arc, and “r” is the radius of the circle

Central Angle Theorem

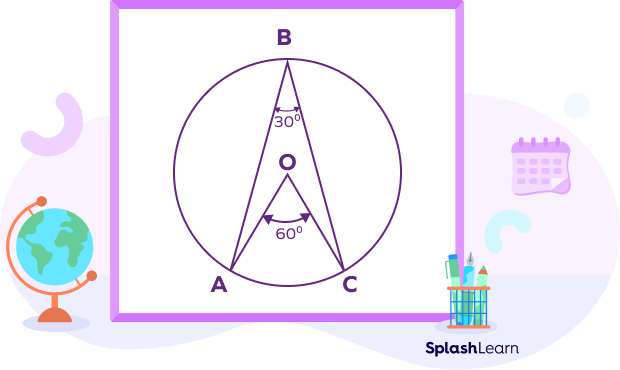
According to the theorem of central angle measure, the angle subtended by an arc at the center of a circle is double the angle subtended by it at any other point on the circle’s circumference.

How to Find the Central Angle?

To calculate the central angle, we must find out the length of the arc and the radius. The below-mentioned steps elucidate how to find the center of the angle:

• Locate the endpoints of the arc and the central point of the circle.
• Connect the endpoints of the arc with the center of the circle. Also, take a measure of the lengths of the arc and the radius.
• Use the formula Central Angle $= \frac{Length of the Arc}{Radius}$  to obtain the measure of the central angle.

How to Find the Central Angle and Intercepted Arc?

Let’s discuss the Intercepted Arc formula and examples. We can find the central angle of a circle using the intercepted arc formula, which states the following:

• Central angle $=$ Measure of the intercepted arc
• 2 (inscribed angle) $=$ Central angle
• 2 (inscribed angle) $=$ Intercepted arc
• Inscribed angle $=$ Half the sum of the intercepted arcs

Solved Examples

1. Supposing Mr. A divides a circle into four equal parts using two diameters, how can we measure the central or inscribed angle of each section of such a circle?

Solution: We know that the complete angle in a circle $= 360$.

Since the circle is divided into 4 equal parts, the angle of each section $= \frac{360}{4}$.

The central angle of each quadrant will be $90^\circ$.

2. If the arc of a circle has a length of 8 cm and the central angle measures $120^\circ$, what will be the radius of such an arc? (Use $\pi = 3.14$)

Solution:

We know that the central angle $= 120^\circ$, and the arc length is 8 inches.

Using the formula, Central Angle $= s \times \frac{360}{2 \pi r}$

where, “s” is the length of the arc, and “r” is the radius of the circle

$120^\circ = 8 \times \frac{360}{2 \pi r}$

$r = \frac{8 \times 360}{2 \pi \times120}$

$r = \frac{2880}{753.6}$

$r = 3.821$

The radius of the arc is 3.821 cm.

3. If an arc length is 11 inches and the radius of a circle is 7 inches, what will be the angle of the arc? (Use $\pi =227$)

Solution: 

Given that length of the arc $= 11$ inches

The radius of the arc $= 7$ inches

We know that

Central Angle $= s \times \frac{360}{2 \pi r}$

where, “s” is the length of the arc, and “r” is the radius of the circle

Central Angle $= \frac{11 \times 360}{2} \times \frac{22}{7} \times 7 = 90^\circ$

The angle will be $90^\circ$.

4. In the circle below, find out the value of “a.”

Solution:

We know that the central angle $=$ intercepted arc

• $4a + 8 = 60$

Solving the equation, we can get the value of a.

The value of a will be 13.

5. In the circle below, find out the measure of $\angle \text{AOB}$.

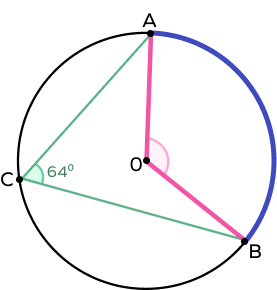
Solution: 

We know that $\angle \text{AOB}$ is a central angle, and $\angle \text{ACB}$ is the inscribed angle.

Also, the central angle is twice the inscribed angle if they are subtended on the same arc.

Thus, $\angle {AOB} = 2 \angle \text{ACB}$

$\angle \text{AOB} = 2(64^\circ)$

$\angle \text{AOB} = 128^\circ$

The measure of $\angle \text{AOB is} 128^\circ$.

Practice Problems

Frequently Asked Questions