Coordinates: Introduction
Coordinates are ordered pairs of points that help us locate any point in a 2D plane or 3D space. You might have seen grids being used in math. What are these grids? These grids help us to plot any point using its coordinates. So, what are coordinates in math? Let us see the meaning of coordinates in math.
Coordinates of a point in a 2D plane, also known as cartesian coordinates, are two numbers or sometimes a combination of a letter and a number that tell us the exact location of a specific point on a grid. Here, the grid is known as a coordinate plane.
A coordinate plane has four quadrants and two axes: the X-axis is the horizontal axis and the Y-axis is the vertical axis.

Recommended Games
What Are Coordinates in Math?
Let us understand the definition of coordinates in math.
Coordinates are a pair of numbers which are used to determine the position of a point or a shape in a 2-dimensional plane.
We define the position of a point on a 2D plane using two numbers, called the x-coordinate and the y-coordinate. The x-coordinate always comes first in the ordered pair followed by the y-coordinate and it determines where the point is in the left–right or horizontal direction, and the y-coordinate determines the position of a point in the vertical, up–down direction.
Ordered Pair
So, how do you write coordinates? The Cartesian coordinates of a point are usually written in parentheses and separated by commas, like (x, y). Note that the order matters while writing the coordinates of a point.
The coordinates are written as an “ordered pair” as shown below. The letter P is simply the name of the point and is used to distinguish it from others.
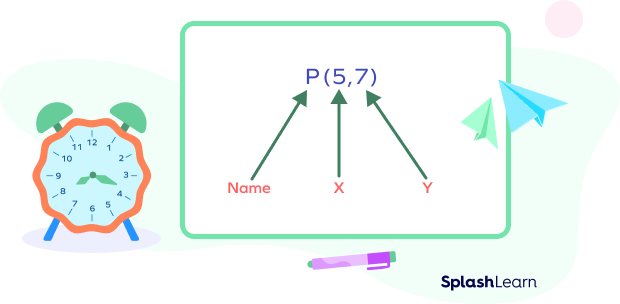
Let us look at examples of coordinates.
Example 1: The point where both the axes intersect is known as the origin.
Coordinates of the origin are written as O(0, 0).
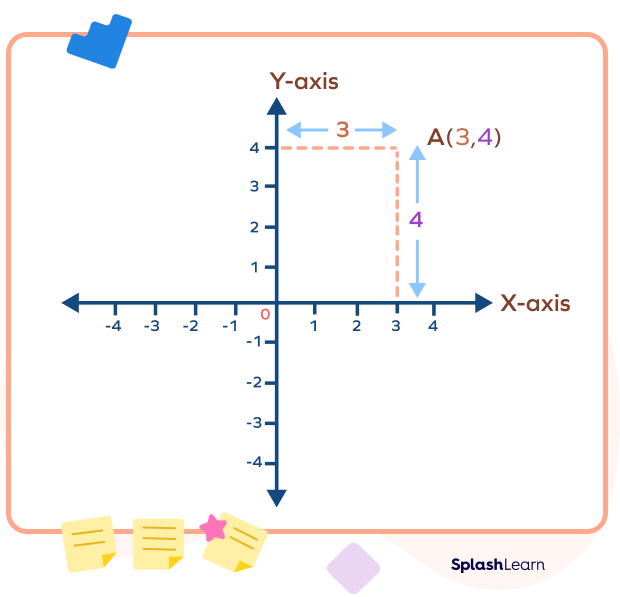
Example 2: In the figure below, the coordinates of point A are (3,4). It means that the point is 3 units along the x-axis and 4 units up.
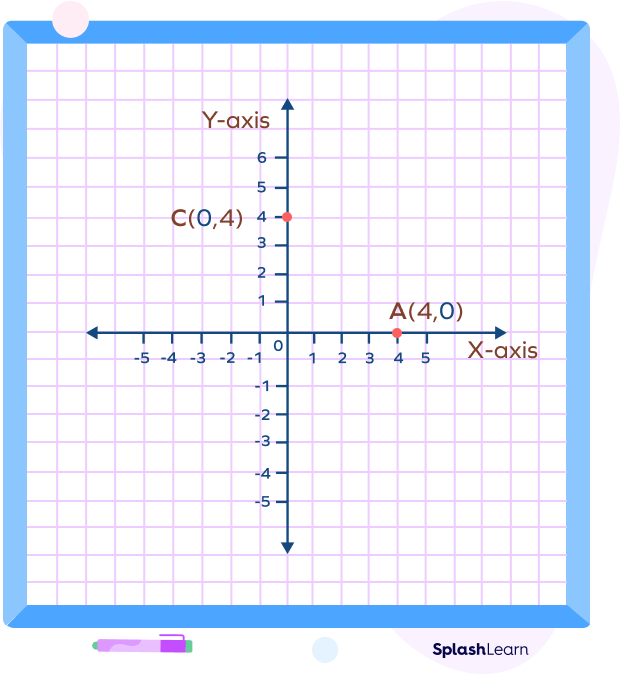
Example 3: Coordinates of a point on X-axis and Y-axis.
For a point lying on the X-axis, the y-coordinate is 0. For a point on the Y-axis, the x-coordinate is 0.
Types of Coordinates
We have two major types of coordinate systems as listed below.
- Cartesian Coordinate System
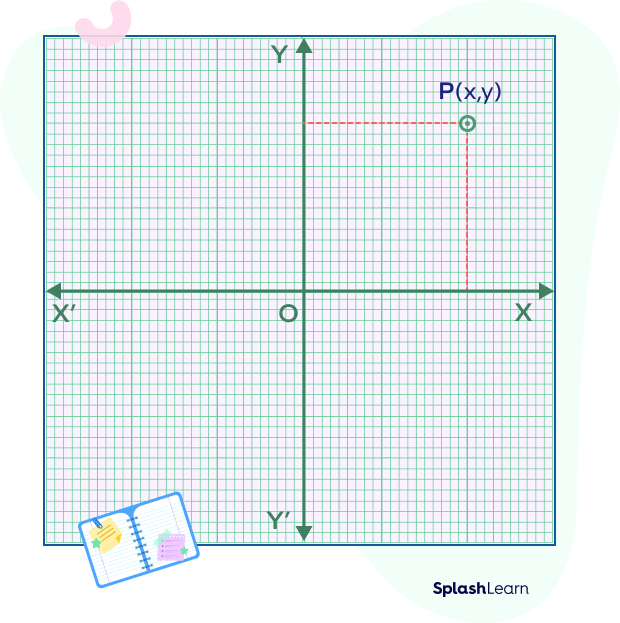
The cartesian coordinate system helps to represent a point uniquely in the n-dimensional coordinate plane. As stated above, it uses the concept of mutually perpendicular lines known as axes, to denote the coordinates of a point. To locate the position of a point P in a plane using two perpendicular lines, the cartesian plane is commonly used. Points are represented in the form of coordinates P(x, y) in two-dimension with respect to x-axis and y- axis.
- Polar Coordinate System
In the polar coordinate system, the origin is considered to be a reference point, called a pole. The position of each point is decided by a distance from the pole and an angle is taken from a reference direction.
Here, we express the coordinates of a point as $(r, θ)$. Simply put, we have two parameters—the angle and the radius.
The coordinate r is the length of the line segment from the point (x,y) to the origin and the coordinate θ is the angle between the line segment and the positive x-axis.
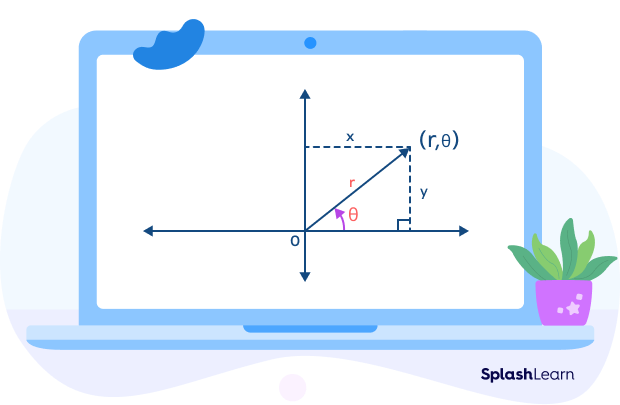
Important Note: From the figure, you can see that $\frac{y}{r} = sin \theta$ and $\frac{x}{r} = cos \theta$.
Thus, we can establish the relationship between the cartesian coordinates and the polar coordinates as:
$x = r$ $cos$ and $y = r$ $sin \theta$
OR
$x^2 + y^2 = r^2$ and $tan \theta = \frac{y}{x}$
Coordinates on a Plane (2D)
A 2D coordinate plane is formed by the intersection of x-axis and y-axis. The two axes intersect at a point O(0, 0) called the origin.
The coordinates indicate the position of a point in the 2D coordinate plane relative to the origin. The x-coordinate of a point is its perpendicular distance from the y-axis measured along the x-axis. The y-coordinate of a point is its perpendicular distance from the x-axis measured along the y-axis.
The coordinates are written as an ordered pair of numbers P(x, y), where P is the name of the point, x refers to the horizontal position and y refers to the vertical position.
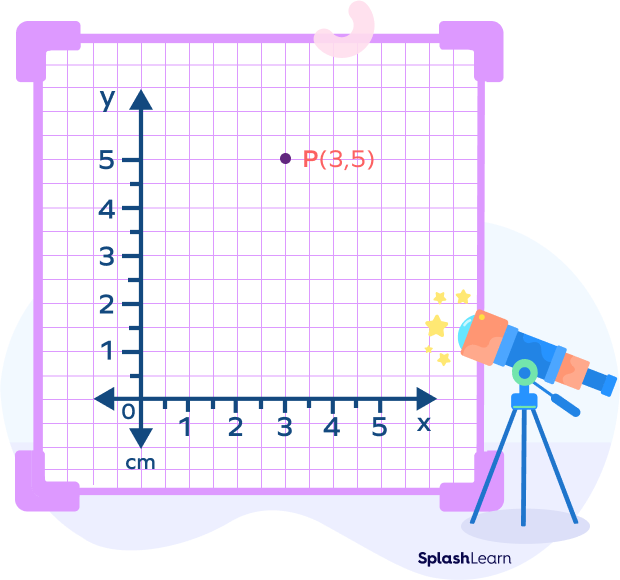
For example, the point P(3, 5) is represented as
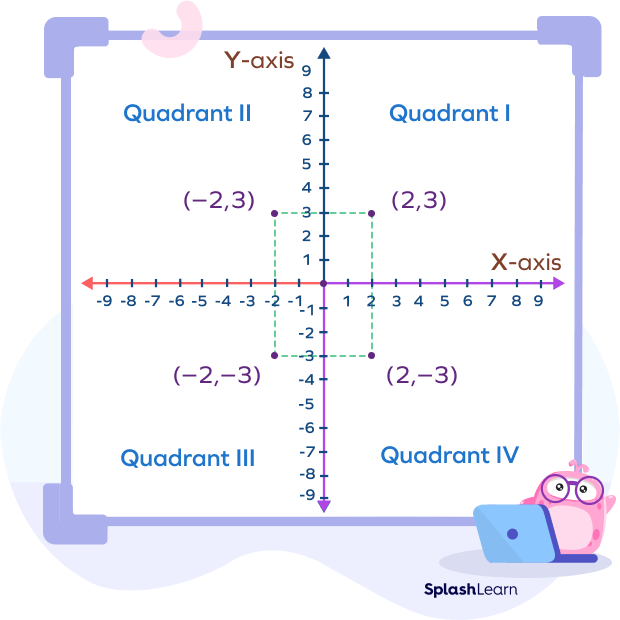
Quadrants in a 2D plane
There are basically 4 quadrants in a 2D plane formed due to the intersection of x-axis and y-axis. They are sometimes named using Roman numerals: I, II, III and IV.
You might wonder if the coordinates rules change based on the quadrants or how they are written in different quadrants. Let’s find out.
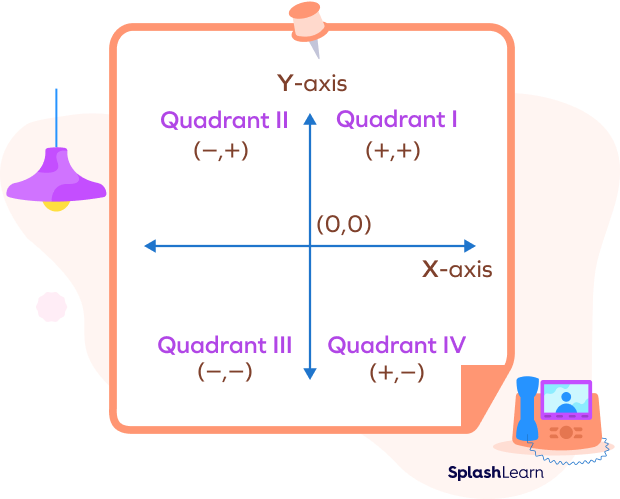
Quadrant 1: It’s the top-right quadrant.
Here, both the coordinates have positive values. For example, P(3, 5), U(8, 4).
Quadrant 2:
Here, x-coordinate has negative values and y-coordinate has positive values. For example, P$(-3, 5)$, U$(-8, 4)$.
Quadrant 3:
Here, both coordinates have negative values. For example, P$(-3, -5)$, U$(-8, -4)$.
Quadrant 4:
Here, x-coordinate has positive values and y-coordinate has negative values. For example, P$(3, -5)$, U$(-8, 4)$.
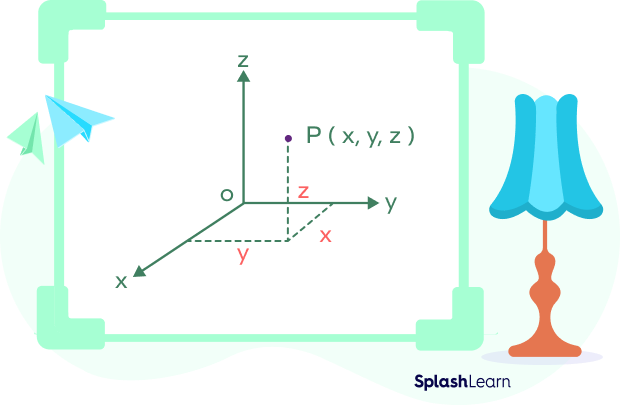
Coordinate in a Space (3D)
A 3D coordinate system can be used to locate the position of a point in 3D space. A 3D coordinate plane is formed by the intersection of three axes—namely the x-axis, y-axis, and the z-axis, which are perpendicular to each other at the origin.
The z-axis can be visualized as an extension to the 2D coordinate plane. Given that the x- and y-axes are the horizontal and vertical axes on a page, the z-axis can be visualized as coming out of, or going through the page, creating the third dimension.
The position of a point in the 3D coordinate plane is quite similar to that of a point in the 2D coordinate plane, with an added z-coordinate: (x, y, z).
How to Read and Plot Coordinates
Coordinates are always written within brackets, with the two numbers separated by a comma (,). Coordinates are ordered pairs of numbers. The first number indicates the point on the x-axis (also known as Abscissa) and the second the point on the y-axis (also known as ordinate).
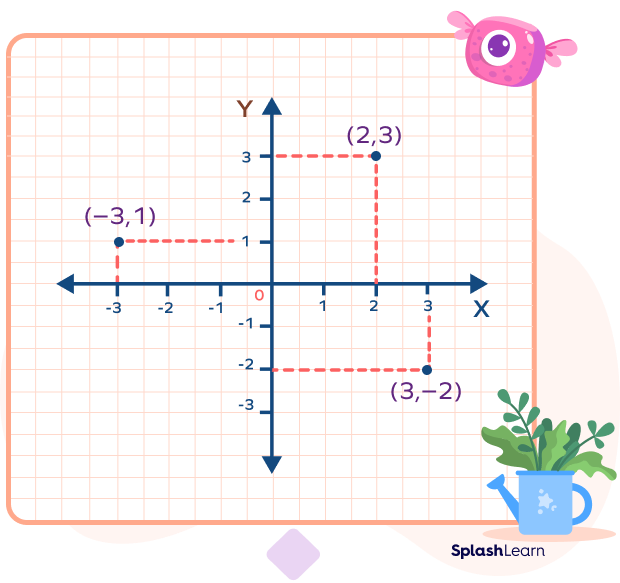
Let’s understand how to plot a point on the coordinate plane with an example.
Example: Plot $(2,3), (3,-2)$ and $(-3,1)$
First, mark the x-coordinate or the horizontal distance along the x-axis and later, mark the vertical distance using the y-coordinate.
Facts
Coordinates hold significance in maps. Often, maps use a letter as one of the coordinates for locating a point, and use a numeral for the other point. Coordinates in a map are given below.

- The x-coordinate of a point is also known as “abscissa.” It is pronounced as ‘‘ab-SISS-ah’’ (the “c” is silent). The term “x-coordinate” is most commonly used.
- The y-coordinate is also called the “ordinate.” You can pronounce it as “ORD-inet.” The term “y-coordinate” is preferred.
Conclusion
In this article, we learned about coordinates of a point, their representation, plotting a point on the cartesian plane along with two types of coordinates.
Solved Examples
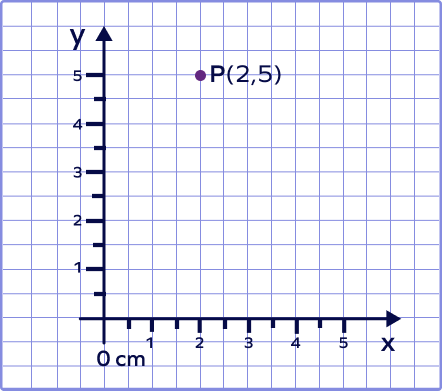
1. Plot the given point on a graph: P(2, 5).
Solution:
Since both the values of x and y are positive, the point lies in the 1st quadrant.
The point is 2 units to the right of origin along the x-axis and 5 units up.
The given point on a graph can be plotted as-
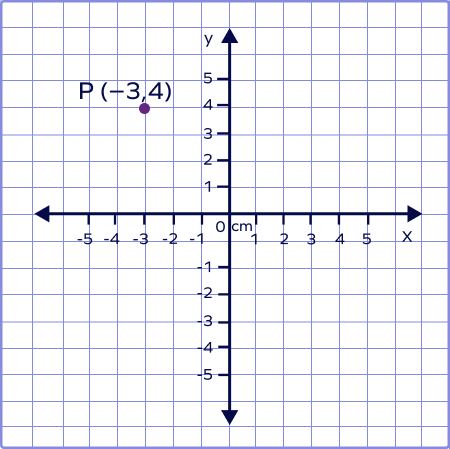
2. Plot the given point on a graph: P$(-3,4)$.
Solution:
Since the value of x is positive and y is negative, hence the point lies in the third quadrant. The given point on a graph can be plotted as:
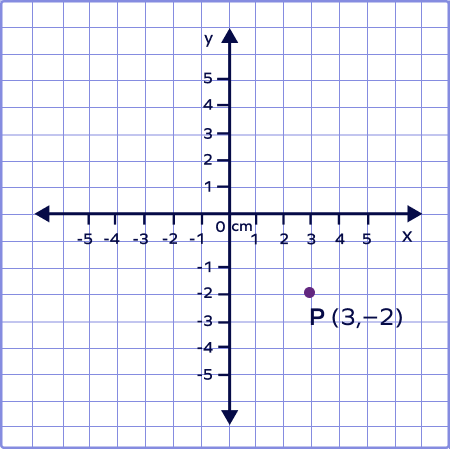
3. Plot the given point on a graph: P$(3, -2)$ and identify the quadrant it lies in.
Solution:
Since both the values of x and y are negative, the point lies in the 3rd quadrant. The given point on a graph can be plotted as:
4. Find the corresponding cartesian coordinates if the polar coordinates of a point are $(2, 30\circ)$.
Solution:
We know that
$x = r$ $cos \theta$ and $y = r$ $sin \theta$
Thus, $x = 2$ $cos30^\circ$ and $y = 2$ $sin30^\circ$
$x = 2 (\frac{\sqrt{3}}{2})$ and $y = 2 (\frac{1}{2})$
$x = \sqrt{3}$ and $y = 1$
Cartesian coordinates are $(\sqrt{3},1)$.
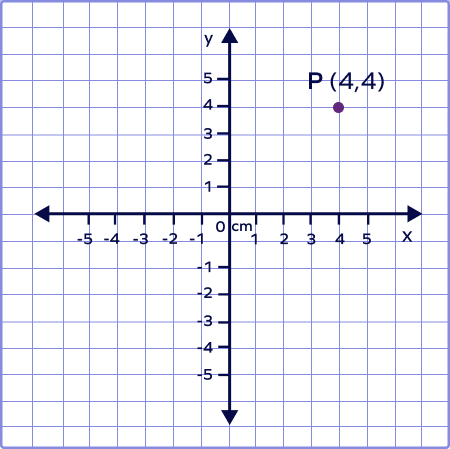
5. Plot the given point on a graph: P(4, 4)
Solution:
Since both the values of x and y are positive, the point lies in the 1st quadrant. The given point on a graph can be plotted as:
Practice Problems
Coordinates
Identify the quadrant in which the point P$(-5, -5)$ lies.
Since both the values of x and y are negative, the point lies in the 3rd quadrant.
What is the “ordinate” in (5, 8)?
The y-coordinate is known as the ordinate. In the ordered pair $(5, 8), 5$ is the abscissa and 8 is the ordinate.
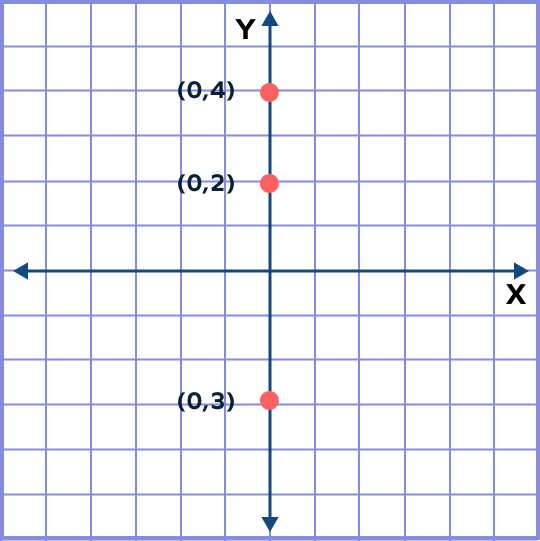
Which of the following points lies on the Y-axis? $(0, 4), (0, 2)$ and $(0, -3)$.
The x-coordinate of all the points is 0. So, all the points lie on the y-axis.
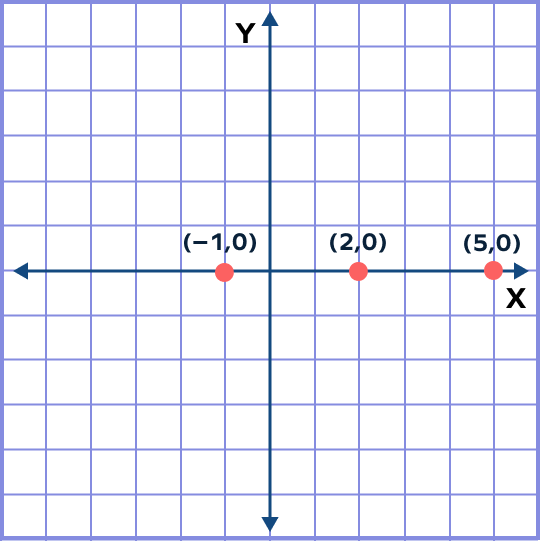
The points $(-1, 0), (2, 0)$ and $(5, 0)$ lie on$ \underline{}$ .
The y-coordinate of all the points is 0. So, all the points lie on the x-axis.
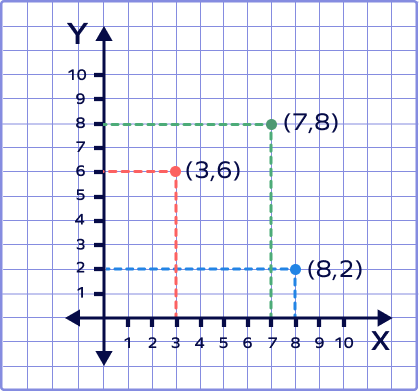
The points $(7, 8), (3, 6)$ and $(8, 2)$ lie on Quadrant$\underline{}$.
The points $(7, 8), (3, 6)$ and $(8, 2)$ have positive coordinates. So, the points lie in the first quadrant.
Frequently Asked Questions
What is the distance formula?
The distance formula is used to calculate the distance between two points.
Let the two points be A and B, having coordinates to be (x1, y1) and (x2, y2), respectively.
Thus, the distance between two points is given as:
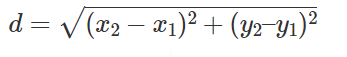
Who invented the Cartesian plane?
René Descartes first published the coordinate system in the seventeenth century.
Which is latitude and longitude in coordinates?
Coordinates are represented as an ordered pair of two numbers. The first number is the latitude and the second is the longitude.
What are three types of coordinate systems?
Three types of coordinates are: cartesian, polar and cylindrical.
What are the uses of cartesian coordinates?
The x- and y-coordinates help us to locate any point in the coordinate axes, to find the distance between the two points and also to find the slope of a line.


















