What Is a Geometric Solid?
A geometric figure or shape that has a three-dimensional structure is known as a geometric solid. They occupy space. In simple words, they have volume. They have length, width, and height.The branch of geometry that deals with three-dimensional (3D) solid shapes is known as solid geometry.
Common examples of solid geometric figures are cone, sphere, cube, cuboid. The geometric solid cube has three dimensions—length, width, and height.
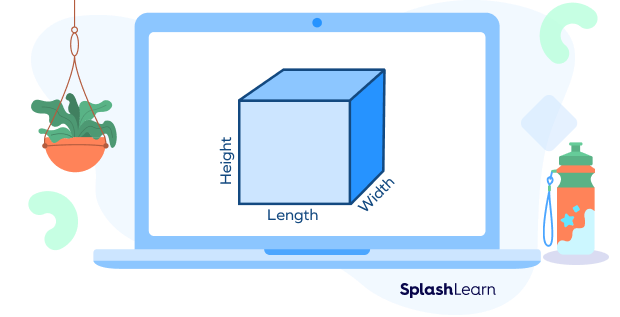
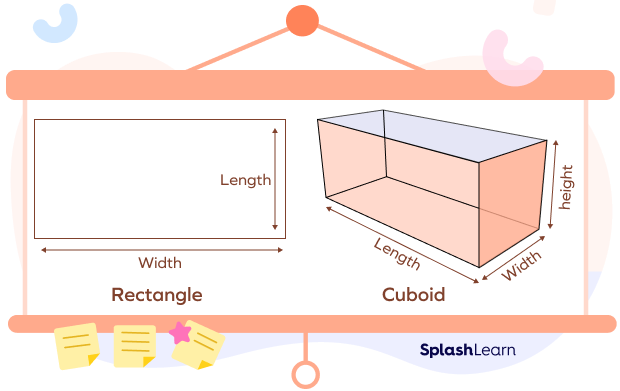
Let’s consider an example to understand the difference between 2D shapes and geometric solids. A rectangle is a two-dimensional shape with only two dimensions, length and width. However, a cuboid is a three dimensional shape that has length, width and height. So, it is a geometric solid.
Recommended Games
Faces, Edges and Vertices
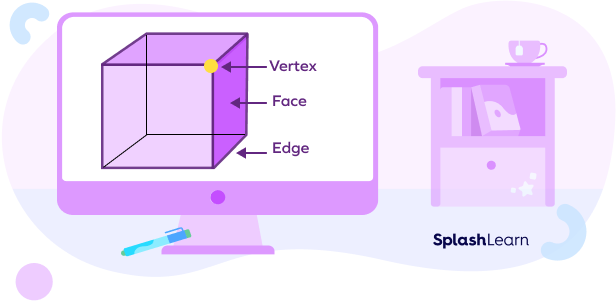
Let’s understand what we mean by face, edge and vertices of geometric solids.
Face: Each flat surface of a solid shape is known as its face.
Edge: The line segment where two faces of a solid shape meet are known as its edge.
Vertices: A vertex is the meeting point of two or more edges of a solid shape. Vertices are the plural form of a vertex.
Recommended Worksheets
Formulas of Solid Geometry
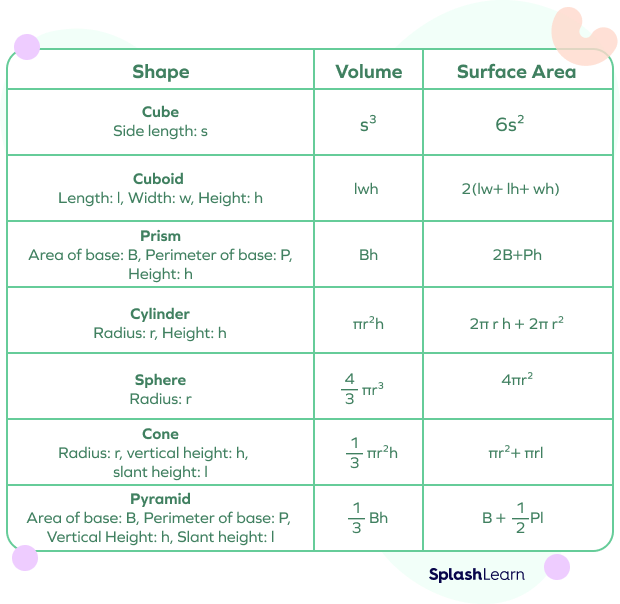
The volume of a geometric solid is the measure of the space it occupies. We express it in cubic units. The surface area of a geometric solid is the sum of the areas of all its surfaces or faces. We express it in square units. The formula for volume and surface area of a few common solid geometric shapes is given below:
Properties of Different Geometric Solids
We can divide geometric solids into two types:
Polyhedrons: Polyhedrons comprises solids that have multiple faces, all of which are flat. Each face is a polygon. Examples include cubes, prism, pyramids, etc.
Non-polyhedrons or Curved Bodies:
Non-polyhedrons include solids with curved surfaces or a combination of curved and flat surfaces. Examples include sphere, cone, cylinder, etc.
Let’s look at some of the important geometric solid shapes and names.
Cube
A cube has 6 faces. Each face is a square. You can consider a cube as a packing box where all the sides are equal.
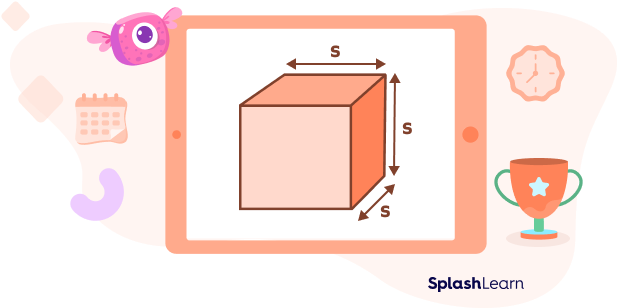
- Properties of a cube:
- All the edges are equal in length.
- All the angles of a cube measure $90^{\circ}$.
- A cube has 8 vertices, 12 edges, and 6 faces.
- Volume of a cube $= side^{3} = s^{3}$
- Surface area of a cube $= 6 \times side^{3} = 6$ $s^{2}$
Cuboid
A cuboid has 6 faces. The faces are rectangular. You can also call it a rectangular prism.
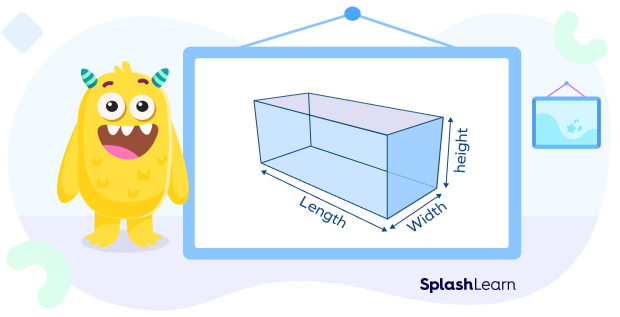
- Properties of a cuboid
- The opposite faces and edges of a cuboid are identical.
- All the edges are not equal in length.
- All the angles of a cuboid measure $90^{\circ}$.
- This solid shape has 8 vertices, 12 edges, and 6 faces.
- Volume of a cuboid $= length \times width \times height = lwh$
- Surface area of a cube $= 2(lw + wh +lh)$
Fun Fact: If the length, height, and width of a cuboid are equal, the cuboid becomes a cube.
Prism
A prism is a solid shape with two identical bases. The lateral faces of a prism are flat surfaces.
The shape and name of a prism depends on the shape of its base.
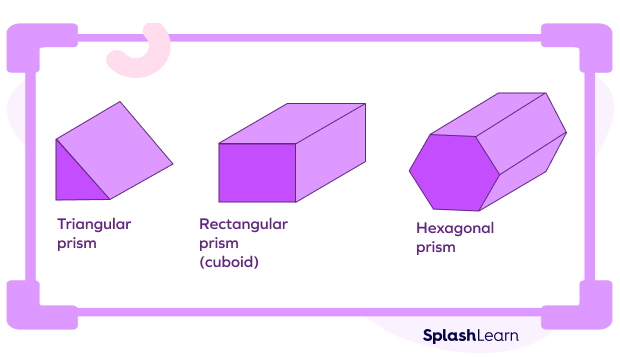
- Properties of a prism:
- A prism has two bases that are identical and parallel.
- The lateral faces of a prism have the shape of a parallelogram.
- A prism having a polygonal base of n sides has (n+2) faces, 2n vertices, and 3n edges.
- Volume of a prism $= Base Area \times Height$
- Surface area of a prism $= (2 \times Base Area) +(Base Perimeter \times Height)$
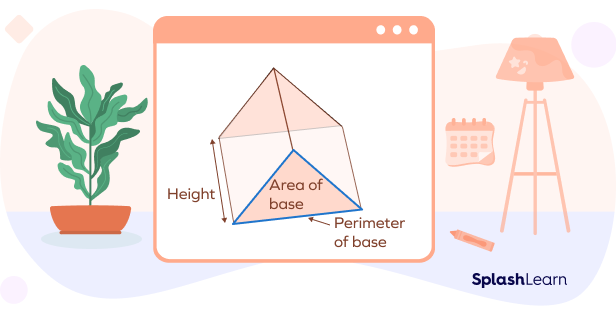
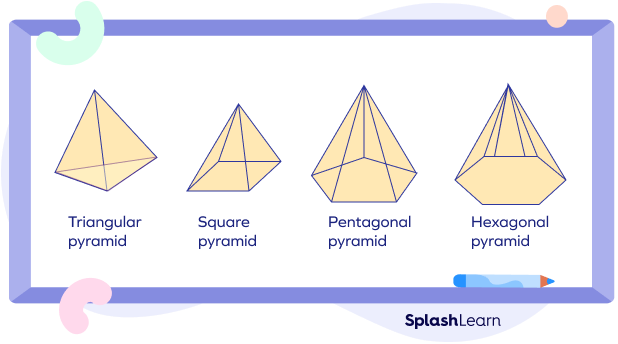
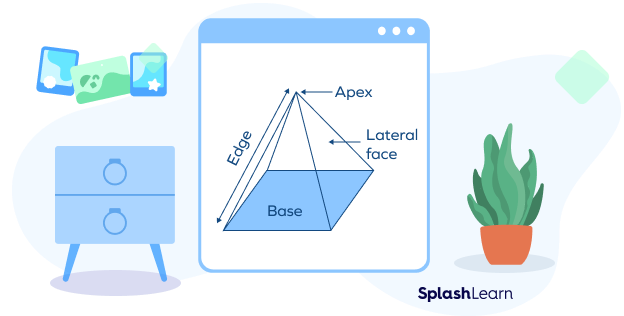
Pyramid
A pyramid is a solid shape that has a flat polygon base. All the other faces of a pyramid are triangles, and they connect at a vertex at the top, called the apex. If the base of a pyramid is a regular polygon, it is called a regular pyramid.
Based on the shape of the base, you can further classify a pyramid as a triangular pyramid, rectangular pyramid, square pyramid, etc.
- Properties of a pyramid:
- A pyramid has just one base, one apex, and multiple lateral faces.
- The number of lateral faces in a pyramid equals the number of sides in its base.
- A pyramid having a polygonal base of n sides has $(n+1)$ faces, $(n+1)$ vertices, and 2n edges.
- Volume of pyramid $= \frac{1}{3} \times Base Area \times Height$
- Surface area of a regular pyramid $= Base Area +(12 \times Base Perimeter \times Slant Height)$
Cylinder
A cylinder is a solid shape with two circular bases. A curved surface connects the two bases.
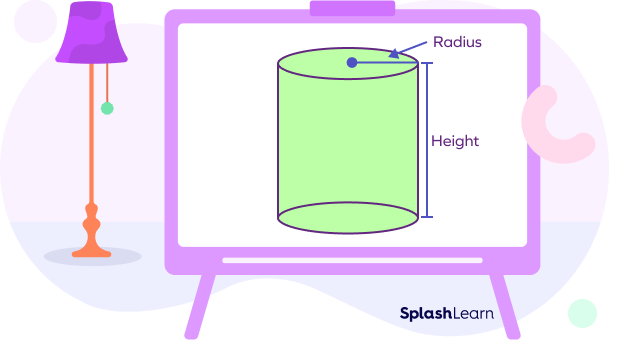
- Properties of a cylinder:
- A cylinder has parallel bases.
- There is no vertex in a cylinder.
- A cylinder has 2 flat faces, 2 edges, and 1 curved surface.
- Volume of a cylinder $= \pi r^{2}$ $h$
- Curved surface area of cylinder $= 2\pi r h$
- Total surface area of cylinder $= 2 \pi r^{2} + 2 \pi rh = 2 \pi r( r + h )$
Cone
A cone is a solid shape with a single circular base and a single vertex. A curved surface connects the base and the vertex in a cone.
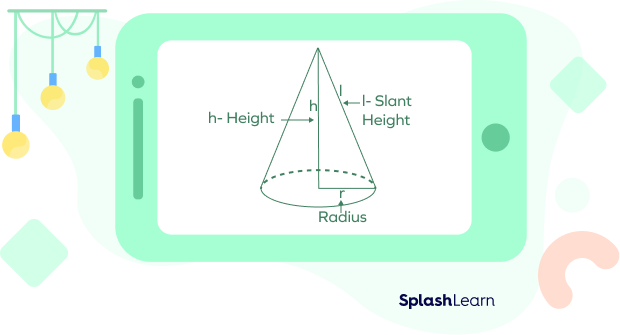
- Properties of a cone:
- A cone has a single curved surface.
- A cone has 1 flat face, 1 vertex, and 1 edge.
- Volume of cone $= \frac{1}{3} \pi r^{2}$ $h$
- Curved surface area of cone $= \pi rl$
- Total surface area of cone $= \pi r^{2} +\pi rl = \pi r( r + l )$
Sphere
A sphere is a solid shape that is perfectly round. The center of a sphere is equidistant from any point on the surface of the sphere.

- Properties of a sphere:
- A sphere has no edges or vertices.
- It does not have a flat face.
- A sphere has just 1 curved face.
- Volume of sphere $= \frac{4}{3} \pi r^{3}$
- Surface area of sphere $= 4 \pi r^{2}$
Geometric Solids Around Us
We often come across different types of solid geometric shapes in our daily life. Some common examples are sugar cubes, bricks, basketball, Rubik’s cube, dice, etc.

Conclusion
Geometric solids are three dimensional geometric shapes. A clear conception of geometric solids will enable kids to build their foundation in geometry. The knowledge will prepare them to understand and learn advanced concepts easily. Explore more at SplashLearn!
Solved Examples
1. Is the figure below a geometric solid?

Solution: The given figure is a geometric solid since it is a three-dimensional shape. It has a cylindrical shape. It has volume and occupies space.
2. Find the surface area of a cube of edge 4 units.
Solution: The surface area of a cube is given by the formula $6$ $s^{2}$. Here, the length of an edge is 4 units.
So, surface area $= 6 \times 4^{2} = 6 \times 16 = 96$ square units.
3. Find the volume of a sphere radius of 21 feet.
Solution: The volume of a sphere is given by the formula $\frac{4}{3} \pi r^{3}$. Here, the radius is 21 feet.
So, volume $= \frac{4}{3} \times \pi \times (21)^{3} = 38808 \text{feet}^{3}$.
4. How many vertices does a cylinder have?
Solution: The cylinder is a solid shape that has zero vertices.
5. A pyramid has a square base. How many faces does the pyramid have?Solution: We know that a pyramid with a base of n sides has $(n+1)$ faces. Here, the base is a square. This means the number of sides is $n = 4$. So, the pyramid has $4 +1 = 5$ faces.
Practice Problems
Geometric Solid – Definition with Examples
Which of the following is not true?
A triangle is a two-dimensional shape. Since it does not have depth, it is not a geometric solid.
Which of the following geometric solid has a flat face as well as a curved surface?
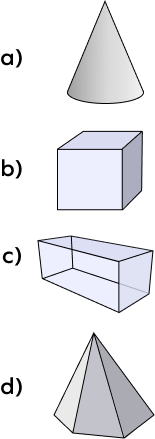
Option (a) has the image of a cone, and we know that a cone has a flat face and a curved surface.
A cuboid has length $= 5$ cm, width $= 2$ cm, and height $= 4$ cm. What is its volume?
The volume of a cuboid is given by the formula V $= length \times width \times height$.
Here, length $= 5$ cm, width $= 2$ cm, and height $= 4$ cm.
So, volume V $= 5 \times 2 \times 4 = 40$ $\text{cm}^{3}$.
What is the number of edges of a pentagonal prism?
A prism of n sides has 3n edges. Here, the prism has a pentagonal base. The number of sides in the base is 5. So, the number of edges is $3 \times 5 = 15$.
Which one of the geometric solids given below has all the angles equal?
The measure of each angle of a cube is 90 degrees.
Frequently Asked Questions
What are polyhedrons?
Polyhedra is the plural term for polyhedron. A polyhedron is a 3D shape with straight edges, flat faces, and sharp vertices.
Do geometric solids have definite volumes?
Yes, geometric solids have definite volumes.
Do circles and spheres mean the same thing in geometry?
No, a circle and a sphere do not mean the same thing in geometry. A circle is a closed 2D figure, while a sphere is a 3D figure. While a circle has no depth, a sphere has depth.
Is a trapezoid a geometric solid?
No, a trapezoid isn’t a geometric solid since it is a 2D figure.
What is an example of a curved solid in real life?
A ping pong or tennis ball are good examples of curved solids in real life.




















