What Is a Nonagon?
A nonagon is a nine-sided polygon or a polygon having 9 sides.
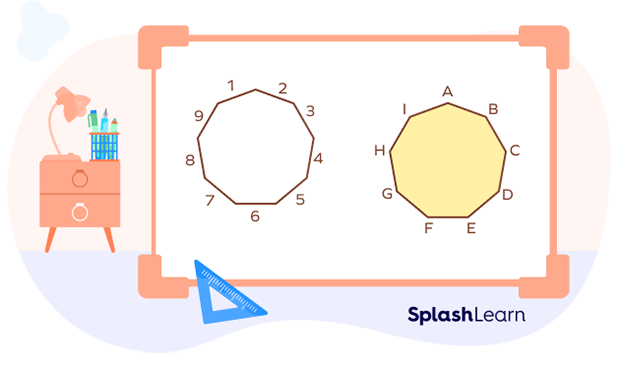
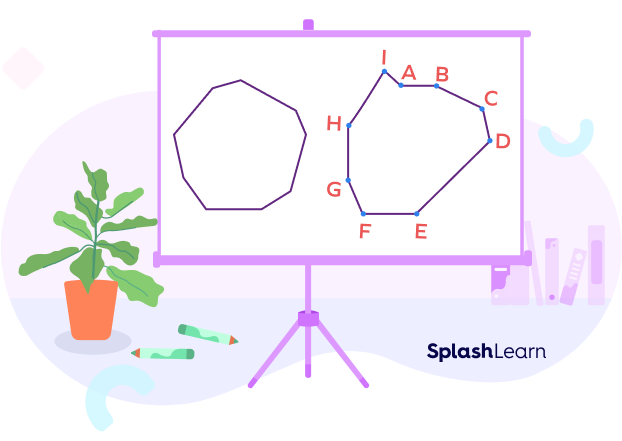
A nonagon has 9 vertices, 9 sides, and 9 interior angles. In the given image, we have a nonagon ABCDEFGHI.
- There are 9 sides. (AB, BC, CD, DE, EF, FG, GH, HI, and IA)
- There are 9 angles. (∠ABC, ∠BCD, ∠CDE, ∠DEF, ∠EFG, ∠FGH, ∠GHI, ∠HIA, and ∠IAB)
- There are 9 vertices. (A, B, C, D, E, F, G, H, and I)
A polygon is a two-dimensional shape that is closed and has a finite number of sides. The sides of a polygon are made of straight line segments. For any polygon, the number of sides equals the number of interior angles.
A polygon is named after the number of sides. For example, a polygon with three sides is called a triangle, a polygon with 4 sides is called a quadrilateral, a polygon with 5 sides is called a pentagon, etc.
Similarly, a polygon with 9 sides is called a nonagon. Note that the sides of a nonagon may or may not be of equal length. Based on the lengths of sides, we classify nonagons as regular and irregular nonagons. We will learn about them later in the article.
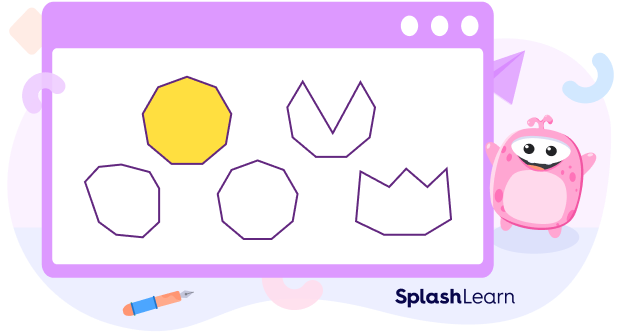
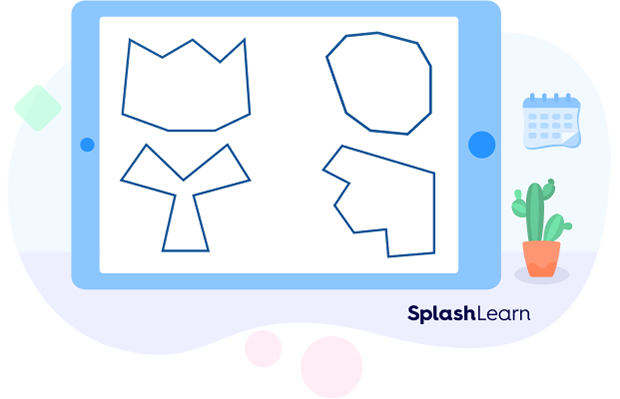
Here are some examples of nonagons!
Nonagon: Definition
In geometry, a polygon having nine sides and nine angles is called a nonagon.
Types of Nonagon
There are three possible ways in which we can classify nonagons that are given below:
- Regular Nonagons and Irregular Nonagons
Regular Nonagons: Nonagons in which all the sides and angles are equal are known as regular nonagons.
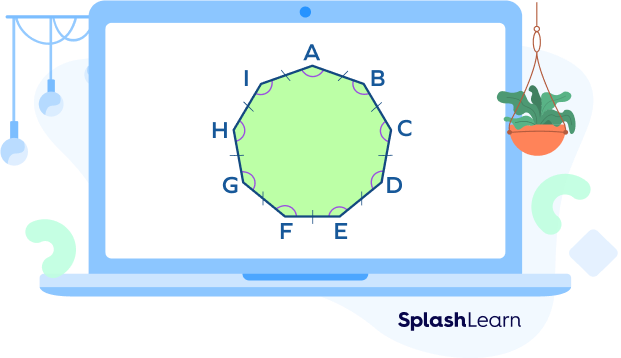
The characteristics of a regular nonagon are as follows:
i) All the sides are equal in length and all the angles are equal in measure.
AB = BC = CD = DE = EF= FG = GH = HI = AI
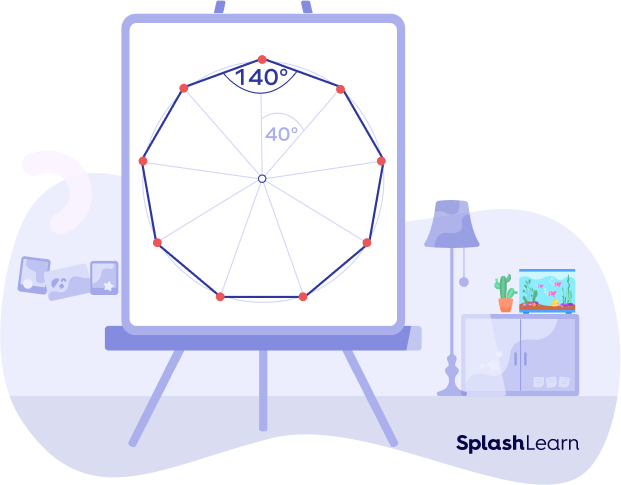
ii) The sum of all interior angles of a nonagon equals 1260°.
Each interior angle of a regular nonagon = 140°
∠A = ∠B = ∠C =∠D = ∠E = ∠F = ∠G = ∠H = ∠I =140°
iii) The sum of exterior angles of a nonagon = 360°
iv) A regular nonagon can be inscribed inside a circle. It means that the vertices of a regular nonagon can lie on the boundary of the circle.
Irregular Nonagons: Nonagons in which sides and angles are not equal are known as irregular nonagons. Examples of an irregular nonagons are given below:
- Convex and Concave Nonagons
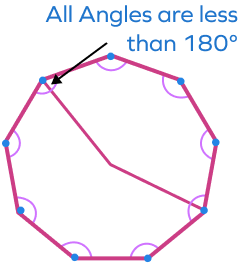
Convex Nonagons: Nonagons in which all the interior angles are less than 180 is known as convex Nonagons. In a convex nonagon, all diagonals lie inside it.
Concave Nonagons: Concave nonagons are the nonagons in which at least one interior angle is greater than 180°. In the concave nonagons, at least one diagonal lies outside it is known as the concave nonagons.
| Convex Nonagon | Concave Nonagon |
|---|---|
 |  |
- Simple and Complex Nonagons
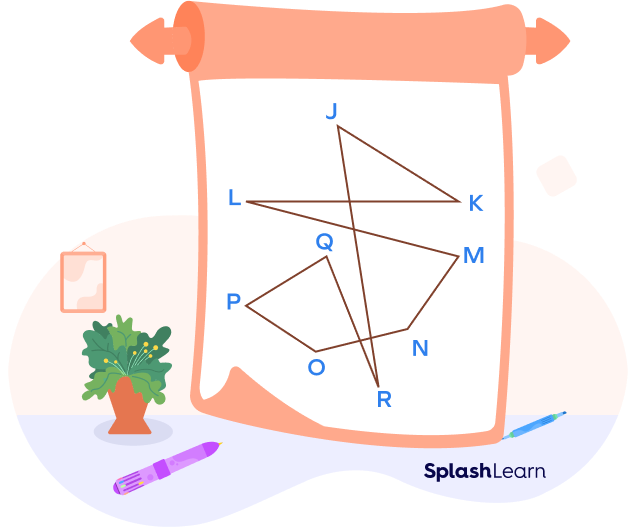
Simple Nonagons: Simple Nonagon is a nonagon which does not intersect itself. Its sides do not cross each other.
Complex Nonagons: Complex nonagons are the nonagons that are self-intersecting and there are additional interior spaces. Its sides cross each other.
Interior Angles of a Regular Nonagon
Each interior angle of a regular polygon $= \frac{180 n – 360}{n}$, where n = the number of sides of the polygon.
For n = 9, interior angle of a regular polygon $= \frac{(180 \times 9) – 360}{9} = 140°$
Sum of Interior Angles of a Nonagon
Sum of interior angles of a polygon $= (n – 2) \times 180°$, where n is the number of sides.
Since the number of sides of a nonagon $= n = 9$, the sum of angles of a nonagon
$= (9 – 2) \times 180° = 7 \times 180° = 1260°$
Thus, the sum of all the interior angles of a nonagon $= 1260°$
Note: To find the sum of interior angles of a polygon, we can also multiply the number of triangles in the polygon by 180°.
Sum of interior angles of a nonagon $= 7 \times 180° = 1260°$
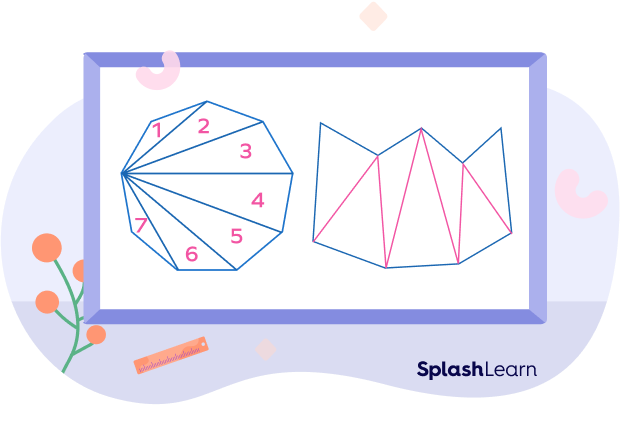
Number of Diagonals in a Nonagon
A diagonal is a line that connects two non-adjacent vertices of a polygon.
Number of diagonals of a polygon $= \frac{n(n – 3)}{2}$ , where n is the number of sides.
For $n = 9$ in a nonagon, we have
Number of diagonals in a nonagon $= \frac{9 \times 6}{2} = 27$
Perimeter of a Regular Nonagon
The total length of the boundary of a polygon is known as the perimeter of a polygon.
If each side of regular nonagon is “a” units, the perimeter of a regular nonagon $= 9 \times a = 9a$ units.
Facts about Nonagon
- The Latin word “nonus” means “ninth.”
- Nonagon is also known as a “9-gon” or a “nine-sided polygon.”
Conclusion
In this article, we learned about nonagons, polygons with 9 sides. We discussed different types of nonagons and important formulas associated with them. Let’s solve a few examples based on these learned concepts.
Solved Examples on Nonagon
1. Find the perimeter of a regular nonagon if the length of a side is 8 units?
Solution:
Number of sides of a nonagon = 9
Length of each side = 8 units
Perimeter $= 9 \times 8 = 72$ units
2. If the perimeter of a regular polygon is 45 units, what will be the length of the side?
Solution:
Number of sides of a regular nonagon = 9 units
Perimeter = 45 units
In regular polygons, all sides are equal in length.
Length of each side = 45 ÷ 9 = 5 units
3. One of the interior angles of a nonagon is 220°. Which type of a nonagon is it?
Solution:
One of the interior angles of a nonagon is 220°.
In a concave polygon, at least one interior angle is greater than 180°.
Since 220° is greater than 180°, it is a concave nonagon.
Practice Problems on Nonagon
What is a Nonagon? Definition, Types, Shape, Examples, Facts, FAQs
Each interior angle of a regular nonagon is
Each interior angle of a regular nonagon is 140°.
The sum of interior angles of a nonagon is ____.
The sum of interior angles of a nonagon is 1260°.
Which of the following is not true about a regular nonagon?
The sum of all angles of a nonagon $= (9 - 2) \times 180 = 1260°$
How many sides does a Nonagon have?
A nonagon has 9 sides.
Frequently Asked Questions about Nonagon
What is the sum of all exterior angles of a nonagon?
The sum of all exterior angles of any polygon is always 360°. So, the sum of all exterior angles of a nonagon will also be 360°.
How do we derive the formula for the number of diagonals of a polygon?
Consider a polygon with n vertices and n sides. Diagonal of a polygon is a line-segment joining two non-adjacent vertices. We can choose 2 vertices from n vertices in nC2 ways $= \frac{n(n – 1)}{2}$ ways. We have to remove the pairs of adjacent vertices from this selection. There are n such pairs possible.
Thus, the number of diagonals $= \frac{n(n – 1)}{2} – n = \frac{n^{2} – n – 2n}{2} = \frac{n^{2} – 3n}{2} = \frac{n(n – 3)}{2}$
How many lines of symmetry does a regular nonagon have?
There are 9 lines of symmetry in a regular nonagon.
Does a regular nonagon possess rotational symmetry?
Yes. A regular nonagon has a rotational symmetry of 40°. The order of rotational symmetry is 9.
















