What Is a Prism?
A prism is a closed solid whose two identical faces are parallel plane polygons and whose side faces are parallelograms or rectangles. All the faces of a prism are flat.
You can find various kinds of prisms. Here are some examples:
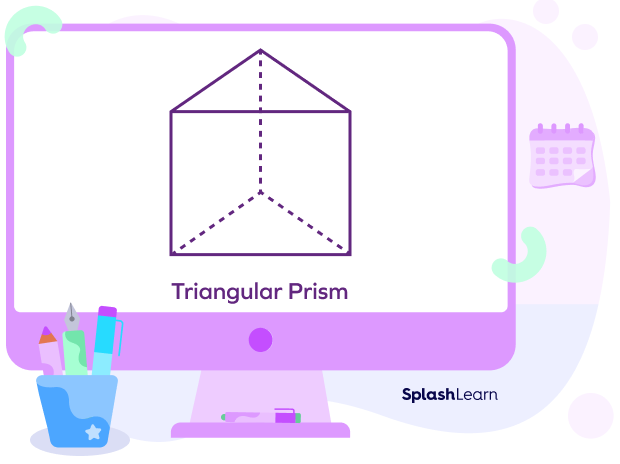
1. Triangular prism, whose base is made up of triangles with 3 rectangular lateral faces.
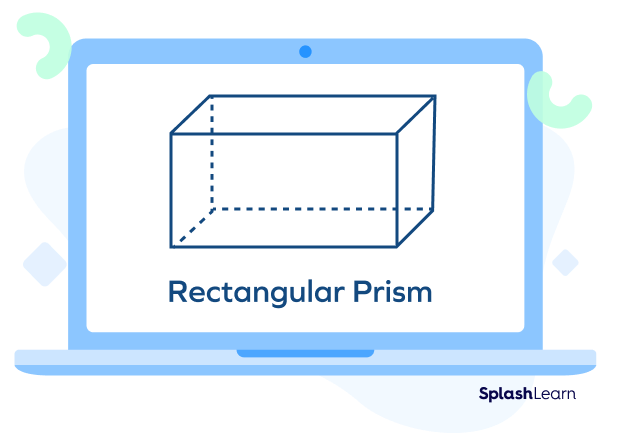
2. Rectangular prism, whose base is made up of rectangles with 4 rectangular lateral faces. It is also known as a cuboid.
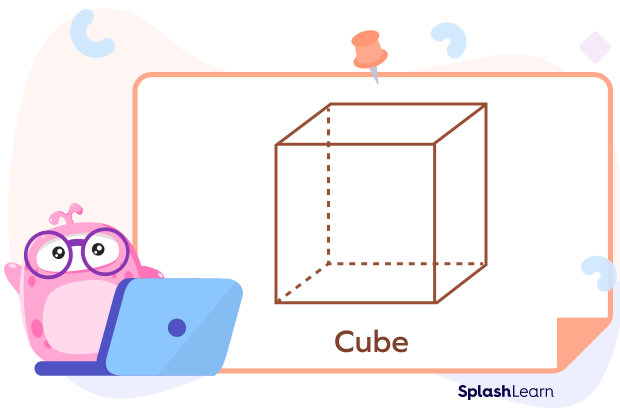
3. Cube, whose base is made up of squares with 4 square lateral faces. It is also known as a square prism.
4. Pentagonal prism, whose base is made up of pentagons with 5 rectangular lateral faces.

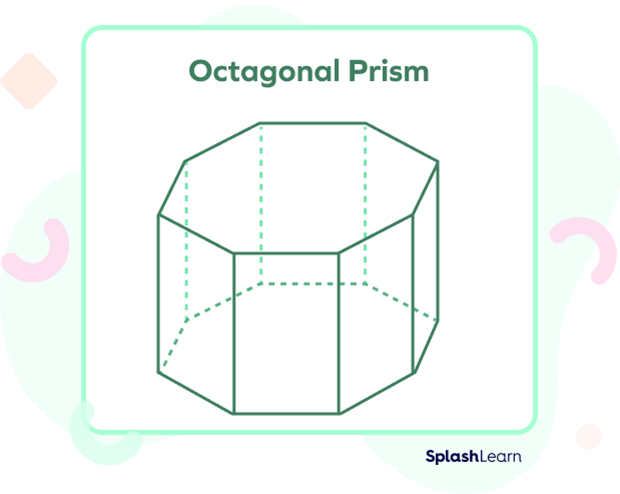
What Is an Octagonal Prism?
An octagonal prism is a prism bounded by 2 octagonal bases and 8 rectangular sides. It has 24 edges, 16 vertices, and 10 faces.
In our day-to-day life, we use and see objects of various octagonal shapes. For example:
- An octagonal platter

- An octagonal pizza box
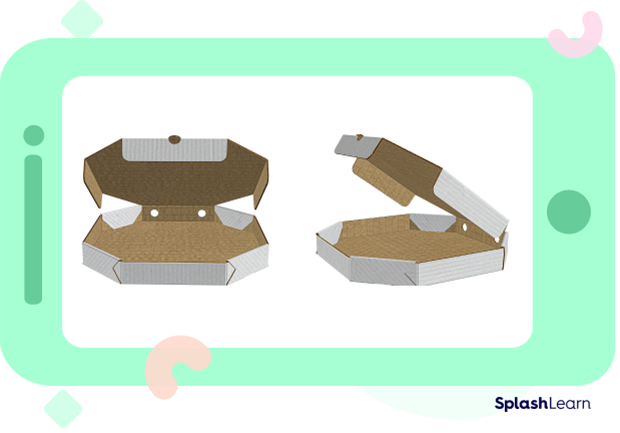
- An octagonal ring

- An octagonal egg container

The Surface Area of an Octagonal Prism
The surface area of an octagonal prism includes the areas or spaces covered by all of its faces. In order to calculate its total surface area, you need to apply the following formula:
Lateral surface area of a right octagonal prism $=$ perimeter of base $\times$ height
Total surface area of an octagonal prism $=$ lateral surface area$ + 2 \times$ base area
The Volume of an Octagonal Prism
Volume is the amount of space a solid shape occupies or the amount of space contained within the shape.
Volume of an octagonal prism $=$ base area $\times$ height
Octagonal Prism with Regular Hexagon as Base
To find the surface area or volume of a regular octagonal prism we will require the side length (s), height (h), and the apothem length (a). The apothem of a regular polygon is a line segment joining the center of the polygon to the midpoint of one of its sides.
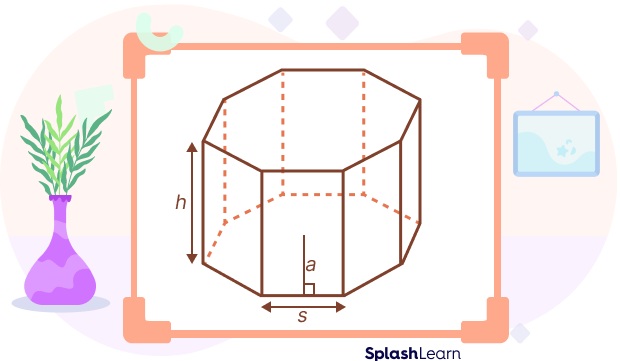
So, perimeter of base $= 8s$
and area of base $=$ perimeter of base $\times$ apothem $\div 2$ or 4sa
Thus, lateral surface area of a right regular octagonal prism $= 8sh$
Total surface area of a regular octagonal prism $= 8sh + 8sa or 8s(h + 1)$
Volume of a regular octagonal prism $= 4sah$
Solved Examples
Example 1: How many faces does an octagonal prism have?
Solution: The faces are the same as the surfaces, which make a 3D shape, so an octagonal prism has 10 faces (8 rectangular faces and 2 octagonal faces$—$one at the top and the other at the bottom).
Example 2: How many edges does an octagonal prism have?
Solution: The edges are the same as the sides, where the two faces meet. Therefore, there are 24 edges in an octagonal prism.
Example 3: How many vertices does an octagonal prism have?
Solution: The vertices are points at the corners of the shape where two edges meet. Thus, an octagonal prism has 16 vertices or corners.
Example 4: What is the volume of the given regular octagonal prism?
Alt Tag: Octagonal prism with 6 m side, 4 m apothem, and 12 m height
Solution: We know that the formula for the area base of an octagonal prism $=$ perimeter $\times$ apothem$\div 2$
The formula for the perimeter of the base of a regular octagonal prism$ = $$8 \times$side
Here, side $= 6 m$, apothem $=$$ 4 m $
So, perimeter $= 8 \times 6 m = 48 m$
Now, the area of base for this octagonal prism$ = $perimeter$ \times$ apothem $\times 2$
$= 48 m \times 4 m \div 2$
$= 96 m²$
Hence, the volume of an octagonal prism $=$ base area $\times$height
$= 96 m² \times 12 m$
$= 1152 m³$
Practice Problems
Octagonal Prism - Definition With Examples
Which among these is one of the properties of a prism?
We call a solid shape a prism when it has identical parallel ends and flat faces, not curved faces.
What is the volume of the given regular octagonal prism?
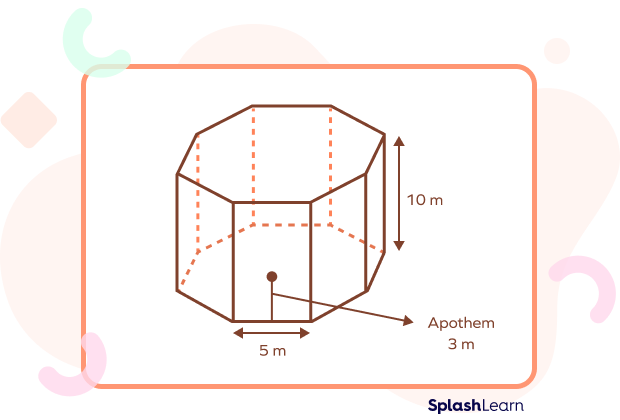
Volume of a regular octagonal prism $= 4 \times$ side $\times$ apothem length $\times$ height
$= 5 m \times 3 m \times 10 m$
$= 600 m³$
An octagonal prism is a ___$-$dimensional polyhedron.
An octagonal prism is a $3-$dimensional polyhedron with 8 rectangular sides and 2 octagonal bases.
Frequently Asked Questions
What do you mean by the surface area of an octagonal prism?
Surface area means the area of the surface it covers. Spaces covered by the faces is known as the surface area of an octagonal prism.
Lateral surface area of a right octagonal prism $=$ perimeter of base $\times$ height
Total surface area of an octagonal prism $=$ lateral area $+$ base area $\times 2$
Why do we consider an octagonal prism a decahedron? Explain with reasons.
In geometry, “deca” means ten. An octagonal prism has 2 octagonal faces and 8 rectangular faces. In other words, we can say it has 10 faces. Hence, we can also call an octagonal prism a decahedron.
Why do we consider an octagonal prism a polyhedron?
Solids that are made up of only polygonal faces joined to each other through vertices are called polyhedrons.
An octagonal prism is made up of only polygonal faces, which are joined to each other through vertices. Hence, an it is a polyhedron.
















