What Is Vertical Volume Liquid?
When Jo drank water from her water bottle on a sunny day, she got curious about something. Jo was curious about the amount of water her water bottle could carry.
As we know, water is shapeless. It takes the shape of the container you put it in. Therefore, if we can find the volume of Jo’s water bottle, we can figure out the volume of water in it. Vertical volume liquid is the volume of a given amount of liquid, i.e., the amount of space a liquid takes up in any container.
Recommended Games
The Volume of Different Shapes
Volume is the product of the surface area of an object and its depth/height, provided it rises uniformly from the base. Look at the figure below:

In the picture above, we get a cylinder when a two-dimensional figure (circle) acquires a depth/ height and rises uniformly from the base. So, we can say that:
The formula for volume of liquid in a vertical cylinder = (area of a circle) πr² × h (height of the cylinder)
Similarly, we have standard formulas for finding the volume of each solid:
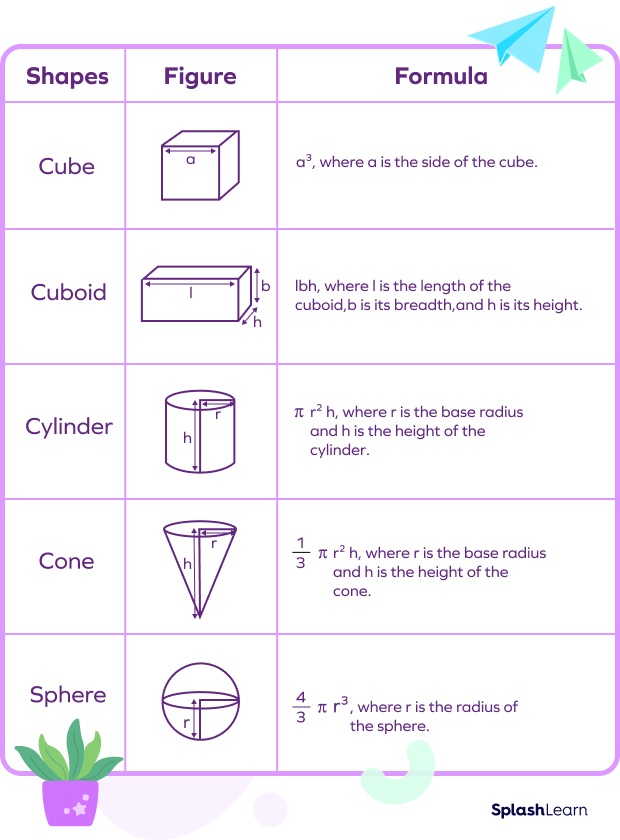
Recommended Worksheets
Solved Examples
Example 1: Find the volume of water that a cubical water tank of length 2 m can hold.
Solution:
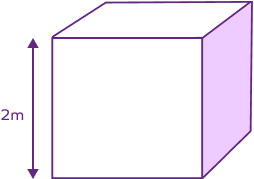
The volume of water the given tank can hold = volume of a cube = $a^3$.
Length of each side of given tank = a = 2 m
So, the volume of water the tank can hold = $a^3$ = 2 × 2 × 2 = 8 cubic meter.
Therefore, the volume of water the given cubical tank can hold is 8 cubic meters.
Example 2: An ice cream scoop over a cone melts completely so that the cone is filled with melted ice cream to the brim. Find the volume of the liquid ice cream in the cone if its height is 12 cm and the base radius is 3.5 cm.
Solution:
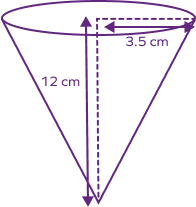
The volume of liquid ice cream inside the ice cream cone = volume of a cone = $\frac{1}{3} πr²h$
Given,
The height of the ice cream cone = h = 12 cm
Base radius of the cone = r = 3.5 cm
Therefore,
Volume of melted ice cream in the cone = $\frac{1}{3} πr²h$
= $\frac{1}{3}$ × 3.14 × 3.5 × 3.5 × 12
= 153.86 cubic cm.
Example 3: Find the volume of water that a cuboidal reservoir of length 4 m, width 2 m, and depth 1 m can hold.
Solution:
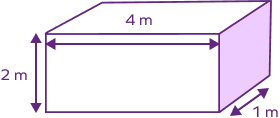
The volume of water a cuboidal reservoir can hold = volume of a cuboid = lbh
Given,
l = 4 m
b = 2 m
h = 1 m
Therefore, the volume of water the given reservoir can hold = 4 × 2 × 1 = 8 cubic meters.
Practice Problems
Vertical Volume Liquid - Definition With Examples
A cylindrical bottle has a base radius of 7 cm and a height of 10 cm. It has water up to the brim. Calculate liquid volume of the vertical cylinder.
The volume of water inside the bottle = Volume of a cylinder $= πr²h$
Given,
$r = 7$ cm
$h = 10$ cm
Therefore,
Volume of the water inside the given bottle $= πr²h = 3.15 × 7 × 7 × 10 = 1538.6$ cubic cm
The volume of water a spherical earthen pot of radius 3 cm can hold is (use $π = 3.14$):
The volume of water the given spherical pot can hold = volume of a sphere = $\frac{4}{3} πr^3$
For the given spherical earthen pot, r = 3 cm.
Therefore,
Volume of water the given sphere can hold = $\frac{4}{3} πr^3 = \frac{4}{3} \times 3.14 \times 3 \times 3 \times 3 = 36 \times 3.14$
= $113.04$ cubic cm.
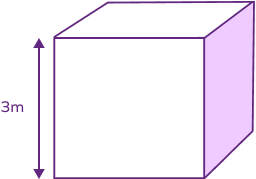
The volume of water a cubical tank of side 3 m can hold is
The volume of water the given tank can hold = volume of a cube = $a^3$
Length of each side of given tank $= a = 3$ m
So, the volume of water the tank can hold = $a^3$ $= 3 × 3 × 3 = 27$ cubic meter
Frequently Asked Questions
Why is the conventional formula of the product of base area and perpendicular height not applicable to finding a cone’s volume?
You can only apply the conventional formula when a solid evenly rises from the base. Cone does not satisfy this condition as it tapers towards the top.
What is the SI unit of volume?
The SI unit of volume in cubic meters.
What is a liter?
“Litre” is a unit measuring the vertical volume of liquid, equal to 1000 cubic meters or one cubic decimeter.
Do two-dimensional shapes have volume?
No, two-dimensional shapes do not have volume.


































