An equation makes use of the “Equal to (=)” symbol to express the relationship of equality between two quantities. Inequalities make use of the “Greater than (>)” and “Less than (<)” symbols to compare quantities that are not equal in nature.
Less than (<):
We use “less than” when one quantity is less than the other quantity. For example, ”8 carrots are less than 10 carrots” can be mathematically expressed as 8 < 10.
Recommended Games
Greater than (>):
We use “greater than” when one quantity is more than the other quantity. For example, ”7 mangoes are more than 3 mangoes” can be mathematically expressed as 7 > 3.
However, in certain cases, when we only have one quantity and we want to make estimates about another quantity comparable with our first one, we use an inequality operator referred to as “Greater Than or Equal To (≥)” or ”Less Than or Equal To(≤).”
Let us understand what is greater than or equal to.
Recommended Worksheets
Greater than or Equal to (≥)
Let’s understand this with the help of a real-life situation. A person must be at least 18 years old to be eligible to vote in an election. It means that a person’s age should be more than or equal to 18 years old to qualify for voting in the USA. The voter’s age can be 22 years or 45 years or 70 years or any other age as long as the age is not less than 18 years.
Let’s say the age of the voter candidate is A.
Then, mathematically, we can say that either A is greater than 18 or A is equal to 18.
A > 18 or A = 18
These two mathematical statements can be combined into one single statement:
A is greater than or equal to 18.
Greater than or Equal to Symbol
When we combine the “>” and “=” symbols to form ≥, we can write the statement as A ≥ 18.
The greater than or equal to symbol is a combination of greater than (>) and equal to (=) sign.
In the greater than or equal to symbol, a horizontal line is placed below the greater than symbol. The symbol is used in mathematical expression for the statements “at least, not less than, and minimum.”

Examples of Greater than or Equal to
x ≥ 2
This example signifies that in the given relation, the value of x is more than 2 or equal to two. It cannot be less than two.
Non Examples of Greater than or Equal to
For example, 4 ≥ 5. Here, the statement ”4 is greater than or equal to 5” is not true as 4 is not greater than 5 nor it is equal to 5.
Greater than or Equal to on a Number line:
Let’s look at the steps on how to represent an inequality of the form x ≥ 3 on a number line.
Step 1: Locate “3” on the number line and mark it with a big circle and fill the circle.
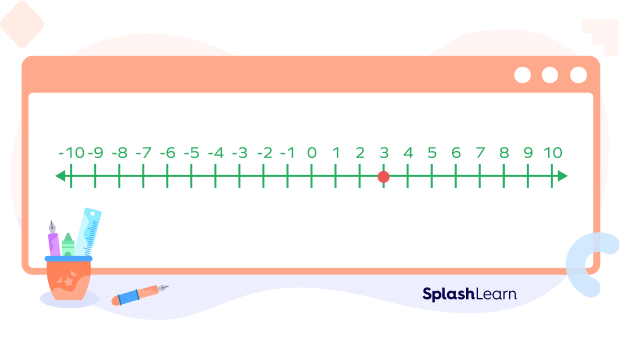
Step 2: The inequality suggests that the variable x is allowed to have any values greater than or equal to 3, that means all the values on the right of this circle. From here, extend an arrow to the right end, signifying all the values the variable x can have.
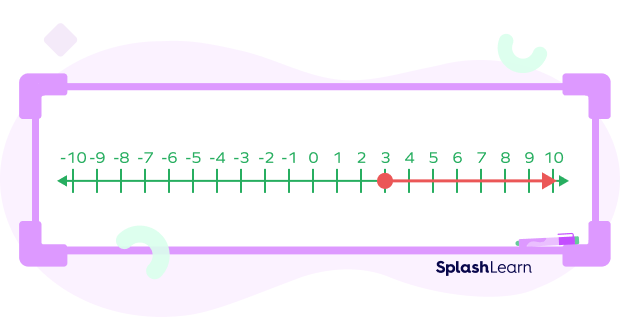
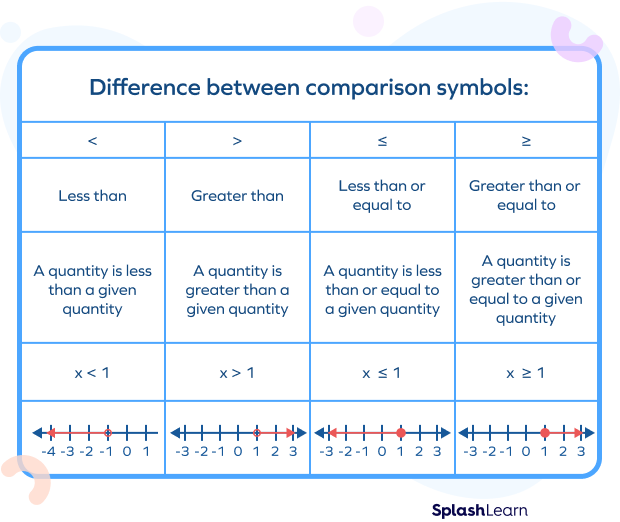
Difference between Comparison Symbols:
Conclusion
We can use greater than or equal to demonstrate that one variable is bigger than or equal to a specific amount when two variables are compared. For example, the company’s strategy is to introduce the product at the same price as before or at a higher price. As a result, we may claim that the new product price is higher than the previous product price—head over to SplashLearn for worksheets on ”greater than or equal to.”
Solved Examples
Q1. Select the numbers greater than or equal to 42 from the given set of the numbers.
44, 23, 0, 7, 55, 33, 61, 42, 66, 12
Solution:
44, 55, 61, 42, 66
Q2. Raashi walks 5 km, Samuel walks 1.5 km, Leo walks 4 km and Alia walks 2 km. Who walked at least 3 km?
Solution:
Raashi and Leo walked at least 3 km.
5 > 3 and 4 > 3
Q3. A minimum of ten pupils per class are required to compete in an Olympiad test. How can you express this situation as a relation?
Solution:
Let x be the number of students required to compete in the test. Then, it is symbolized by the relation: x ≥ 10.
Q4. Graph y ≥ 2 on the number line.
Solution:
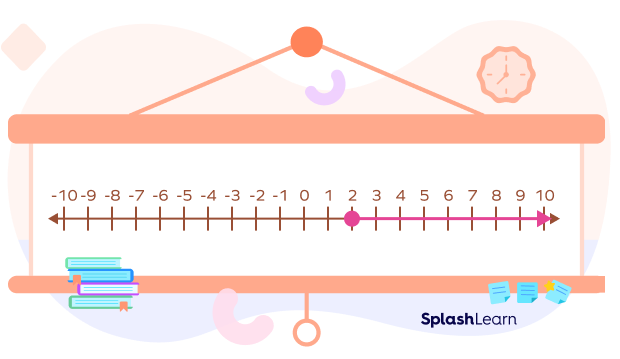
Practice Problems
Greater Than Or Equal To
Select all the possible values from the following that b can have if b ≥ 7
10 > 7. All other options are less than 7.
Identify the number line that best describes greater than equal to −1.




Since all the number towards the right of -1 are greater than -1. The given number line represents all the numbers greater than equal to -1.

To make a jug full of mango juice at least 15 mangoes are needed. Harrison has 10 mangoes, Gary has 20 mangoes, Abram has 17 mangoes and Ahmad has 14 mangoes. Who will be able to make a jug full of mango juice?
20 > 15 and 17 > 15
Which of the following options cannot be the solution of k ≥ 10
1, 2 and 3 are less than 10. So, the given set of numbers does not satisfy the condition.
Frequently Asked Questions
What are the symbols for greater than and greater than or equal to?
The symbol > stands for greater than, whereas the symbol ≥ stands for greater than or equal to.
What is the distinction between less than or equal to and greater than or equal to?
Greater than or equal to indicates that the quantity on the left side should be bigger than or equal to the quantity on the right side, while less than or equal to indicates that the quantity on the left side should be less than or equal to the quantity on the right side.
Is two greater than or equal to three?
We can’t state that 2 is more than or equal to 3 because it’s not true. Neither is 2 greater than 3 nor is it the same as 3. As a result, the right statement is “2 is less than 3.”
When is it okay to use the greater than and less than symbols?
In general, the symbols greater than and less than are employed to denote inequality expressions.
Is −0.2 less than 0.2, and if so, what is the mathematical representation?
Yes, −0.2 is less than 0.2. Therefore, −0.2 < 0.2 is the mathematical representation for the given statement.




































